Cho biểu thức như sau:

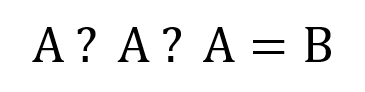
Hãy điền phép tính +, -, * vào ? để được biểu thức đúng.

Dữ liệu vào từ tệp văn bản: dienpheptinh.inp

• Dòng đầu tiên chứa số nguyên dương ~A~.
• Dòng đầu tiên chứa số nguyên dương ~B~.
• Dữ liệu đầu vào luôn đảm bảo có cách điền dấu phù hợp.

Kết quả ghi ra tệp văn bản: dienpheptinh.out

• In ra hai kí tự theo thứ tự là dấu của phép tính tương ứng. Có thể có nhiều cách điền, chỉ cần in ra cách điền đúng bất kì. Mỗi kí tự in trên một dòng (dòng đầu tiên là phép tính ở dấu hỏi đầu tiên, dòng thứ hai là phép tính ở dấu hỏi thứ hai).

Chú ý: dấu nhân là kí tự sao (*)

Ràng buộc

• Có ~60\%~ số test thỏa mãn: ~A, B \le 10^3~;
• Có ~20\%~ số test thỏa mãn: ~A, B \le 10^9~;
• Có ~20\%~ số test thỏa mãn: ~A, B \le 10^{18}~;

Ví dụ

Input

3
6

Output

*
-

Giải thích

~3*3-3=6~

Châu và Huy là đôi bạn thân. Vì yêu âm nhạc nên họ gửi cho nhau lyrics của các bài hát. Cụ thể đó là những xâu ~S~ độ dài ~N~ và chỉ gồm các kí tự từ ~a~ đến ~z~. Để làm cho những xâu này trở nên hay hơn, Huy đã đưa cho Châu một số nguyên dương ~K~ và nhờ thực hiện những thao tác sau. (Lưu ý mỗi thao tác bắt buộc phải làm một lần duy nhất):

• Tạo ra xâu ~T~ từ xâu ~S~ đã cho bằng cách viết ~K~ lần liên tiếp xâu ~S~ liên kề nhau. (Ví dụ ~K = 2~ và xâu ~S~ là ~hello~ thì khi viết sẽ cho xâu ~T~ là ~hellohello~).
• Chọn một chữ cái ở vị trí bất kì trong xâu ~T~, giả sử là vị trí ~i~. Biến đổi tất cả các chữ cái trong xâu ~T~ giống với chữ cái ở vị trí ~i~ thành chữ cái ở vị trí ~i-1~ hoặc chữ cái ở vị trí ~i+1~ (Tất nhiên nếu ở vị trí đầu tiên sẽ không có ~i-1~ và vị trí cuối cùng sẽ không có ~i+1~ để mà biến). Gọi ~X~ là số lần xuất hiện của chữ cái xuất hiện nhiều nhất trong xâu vừa tạo. Phải đảm bảo thao tác biến đổi vừa rồi tạo ra ~X~ lớn nhất.

Yêu cầu:

• Cho xâu ~S~ độ dài ~N~ và số ~K~. Tạo ra xâu ~T~ mới bằng viết liền xâu ~S~ cạnh nhau ~K~ lần. Sau đó thực hiện thao tác như đã miêu tả trong đề sao cho số lần xuất hiện của chữ cái xuất hiện nhiều nhất là lớn nhất và cho biết số lần xuất hiện là bao nhiêu.

Dữ liệu vào từ tệp văn bản: amnhac.inp

• Dòng đầu tiên là 2 số nguyên dương ~N~ và ~K~. ~(N \le 10^6, K \le 10^9)~
• Dòng thứ hai là xâu ~S~ chỉ gồm các kí tự từ ~a~ đến ~z~.

Kết quả ghi ra tệp văn bản: amnhac.out

• In ra một số nguyên duy nhất là số lần xuất hiện của chữ cái xuất hiện nhiều nhất sau các thao tác đã nêu trong đề.

Ràng buộc:

• Có ~20\%~ số điểm với ~N * K \le 10^3~
• Có ~30\%~ số điểm với ~K = 1~.
• ~50\%~ số điểm còn lại không có ràng buộc gì thêm.

Ví dụ

Input 1

10 1
bbabdcccaa

Output 1

6

Input 2

3 2
abc

Output 2

4

Giải thích

Ở ví dụ ~1~, ta được xâu ~T~ là ~bbabdcccaa~. Sau đó biến tất cả kí tự ~a~ thành ~c~ vì ở vị trí thứ ~8~ kí tự ~c~ liền kề với kí tự ~a~ ở vị trí ~9~ và được xâu mới là ~bbcbdccccc~. Ta được 6 kí tự ~c~ trong xâu mới này nên kết quả in ra là 6.

Ở ví dụ ~2~, ta được xâu ~T~ là ~abcabc~. Sau đó biến tất cả kí tự ~a~ thành ~c~ vì ở vị trí thứ ~3~ kí tự ~a~ liền kề với kí tự ~c~ ở vị trí ~4~ và được xâu mới là ~cbccbc~. Ta được 4 kí tự ~c~ trong xâu mới này nên kết quả in ra là 4.

Marisa có ~n~ tấm gỗ và sẽ sửa lại chúng để sử dụng, tấm gỗ thứ ~i~ sẽ có độ đẹp là ~A_i~ hoặc ~B_i~ (tuỳ vào mục đích sử dụng mà Marisa sẽ sửa chúng khác nhau).

Marisa dự định chọn ra ~k~ tấm gỗ để làm hàng rào bao quanh nhà. Trong đó, cô sẽ chọn ra ~k-1~ tấm để dựng hàng rào và ~1~ tấm để làm cửa. Khi đó, những tấm để làm hàng rào sẽ có độ đẹp là ~A_i~ và tấm để làm cửa sẽ có độ đẹp là ~B_i~.

Marisa đang cân nhắc số lượng tấm gỗ sử dụng để làm hàng rào, nên cô sẽ hỏi bạn ~q~ câu hỏi, mỗi câu hỏi là một số nguyên ~k~, hãy giúp cô tính độ đẹp lớn nhất có thể khi sử dụng ~k~ tấm gỗ.

Dữ liệu vào từ tệp văn bản: xayhangrao.inp

• Dòng đầu tiên gồm hai số nguyên ~n,q~.
• Dòng thứ hai gồm ~n~ số nguyên ~A_i~.
• Dòng thứ ba gồm ~n~ số nguyên ~B_i~.
• Dòng thứ tư gồm ~q~ số nguyên ~k~ theo thứ tự, mô tả các truy vấn.

Kết quả ghi ra tệp văn bản: xayhangrao.out

• In ra ~q~ số nguyên, số nguyên thứ ~i~ là đáp án truy vấn thứ ~i~.

Ví dụ

Input 1:

3 1
3 5 4
5 8 5
3

Output 1:

15

Input 2:

3 2
3 5 4
5 8 5
3 2

Output 1:

15 12

Giới hạn: Trong mọi test: ~1 \le n,q \le 10^5, 1 \le A_i, B_i \le 10^9~.

• Subtask 1 (25% số điểm): Marisa chỉ hỏi bạn một câu hỏi duy nhất với ~k = n~.
• Subtask 2 (25% số điểm): ~1 \le n,q \le 10~.
• Subtask 3 (25% số điểm): ~1 \le n,q \le 1000~.
• Subtask 4 (25% số điểm): Không có giới hạn gì thêm.

Vào năm ~3202~, trò chơi "Fake Pyramid" đang vô cùng thịnh hành với giới trẻ.

Trong trò chơi này, bạn được nhận một mảnh giấy kẻ ~n~ dòng và ~m~ cột, tạo ra ~n \times m~ ô vuông. Ô ở hàng ~i~ và cột ~j~ được gọi là ô ~(i,j)~. Mỗi ô ~(i,j)~ đều có một giá trị là ~a_{i,j}~, nếu ~a_{i,j} = 0~ thì nghĩa là ô đó đã bị "cấm", ngược lại, ~a_{i,j}~ sẽ mang một giá trị nguyên dương.

Bạn cần tìm cách vẽ ra một kim tự tháp trên mảnh giấy được cho theo luật như sau (do vẽ trên giấy nên có thể sẽ khác so với tưởng tượng):

• Đầu tiên, bạn chọn ra hai giá trị ~A,B~ thỏa mãn ~1 \le A \le B \le n~.
• Với mỗi ~i~ thuộc đoạn ~[A,B]~, bạn chọn ra hai giá trị ~L_i,R_i~ thỏa mãn ~1 \le L_i \le R_i \le m~. Bạn cần chọn các giá trị ~L_i,R_i~ này sao cho với mọi ~i \in [A,B-1]~, ~L_i \ge L_{i+1}~ và ~R_i \le R_{i+1}~
• Sau khi chọn xong các giá trị, bạn sẽ thu được một kim tự tháp được tạo bởi các ô ~(i,j)~ thỏa mãn ~i \in [A,B]~ và ~j \in [L_i,R_i]~.
• Nói cách khác, với mỗi hàng từ ~A~ tới ~B~, bạn sẽ cần chọn ra một số ô liên tiếp sao cho các ô ở hàng dưới trùm lên các ô ở hàng trên.
• Để tăng độ khó cho trò chơi, kim tự tháp của bạn vẽ ra không được chứa ô nào bị cấm.
• Giá trị của một kim tự tháp chính là tổng giá trị các ô nó chứa.

Ví dụ, cho mảnh giấy ~5 \times 5~ có minh họa như sau:

Ta chọn:

• ~A = 1; B = 3~.
• ~L_1 = 1; R_1 = 1~.
• ~L_2 = 1; R_2 = 3~.
• ~L_3 = 1; R_3 = 3~.

Sẽ thu được kim tự tháp thỏa mãn ở dưới (những ô màu cam là những ô nằm trong kim tự tháp):

Dưới đây cũng là một kim tự tháp thỏa mãn:

Tuy nhiên, hình ảnh dưới đây lại không phải một kim tự tháp thỏa mãn do chứa ô có giá trị ~a(i,j) = 0~ (ô bị cấm):

Cuối cùng, ta có minh họa dưới đây cũng không phải một kim tự tháp do ~L_4 < L_5~

MoHuymed Salah rất hứng thú với trò chơi này, nhưng do anh đang bận rộn với định lý một mùa dài ~7~ năm của mình nên dù đã có một mảnh giấy nhưng chưa có thời gian để tìm ra lời giải tối ưu nhất. Bạn hãy giúp anh ấy nhé.

Yêu cầu: Cho ma trận ~n \times m~ miêu tả mảnh giấy, hãy tìm cách vẽ kim tự tháp sao cho thu được tổng lớn nhất có thể.

Dữ liệu vào từ tệp văn bản: kimtuthap.inp

• Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~m~ ~(1 \le n,m \le 2000)~.
• ~n~ dòng tiếp theo, dòng thứ ~i~ chứa ~m~ số nguyên dương ~a_{i,1}, a_{i,2}, ..., a_{i,m}~ miêu tả mảng giá trị ~a~ ~(a_{i,j} \le 50)~.
• Dữ liệu đảm bảo luôn luôn tồn tại ít nhất một giá trị ~a(i,j) \neq 0~.

Kết quả ghi ra tệp văn bản: kimtuthap.out

• In ra một số nguyên là giá trị lớn nhất có thể đạt được của một kim tự tháp.

Ràng buộc

• Có ~15\%~ số test thỏa mãn: ~n = 1~.
• Có ~20\%~ số test thỏa mãn: Nếu hàng ~i~ ~(1 \le i \le n)~ có ô bị cấm, thì tất cả các ô trong hàng đó cũng đều bị cấm.
• Có ~20\%~ số test thỏa mãn: ~n,m \le 60~.
• Có ~25\%~ số test thỏa mãn: ~n,m \le 300~.
• ~20\%~ số test còn lại không có ràng buộc gì thêm.

Ví dụ

Input 1

5 5
5 0 1 4 4
7 12 6 5 4
5 7 8 0 1
1 6 4 5 0
1 0 7 5 8

Output 1

66

Input 2

5 3
1 1 2
0 0 0
1 2 3
2 3 4
0 0 0

Output 2

15

Giải thích

Ở ví dụ ~1~, ta lấy kim tự tháp theo hình dưới đây:

Còn đây là kim tự tháp ta cần lấy ở ví dụ ~2~:

Cho một dãy ~a~ gồm ~n~ phần tử phân biệt. Chúng ta được thực hiện thao tác sau vô số lần: di chuyển một phần tử ra khỏi dãy, sau đó chèn nó vào một vị trí bất kì trong dãy. Yêu cầu: Hãy tìm số lần thực hiện thao tác ít nhất để đưa dãy về dãy tăng dần.

Input

• Dòng đầu tiên gồm số nguyên ~n~ miêu tả số lượng phần tử.
• Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy ~a~.

Output

• Gồm một dòng duy nhất là kết quả bài toán.

Constraints

• ~1 \le n \le 10^5~
• ~1 \le a \le 10^9~

Sample Input 1

5
1 5 4 2 3 

Sample Output 1

2

Explanation 1

• Chèn số ~4~ vào sau số ~3~ thu được dãy : 1 5 2 3 4
• Chèn số ~5~ vào sau số ~4~ thu được dãy : 1 2 3 4 5
• Tổng cộng hết hai thao tác.

Nhà máy sữa CodeMilk có ~N~ đại lý được xây dựng trên một con đường thẳng. Có thể mô tả con đường là một trục tọa độ, nhà máy sữa nằm tại vị trí gốc tọa độ, ~N~ đại lý ở tại các vị trí có tọa độ ~x_1,x_2,…,x_N~ ~(0 <x_1<x_2<⋯<x_N < 10^9)~, đại lý thứ ~i~ ~(i = 1,2,3,...,N)~ có vị trí tại tọa độ ~x_i~. Nhà máy có M chiếc xe dùng để vận chuyển sữa. Chiếc xe thứ ~i~, chuyển sữa từ đại lý ~s_i~ đến đại lý ~f_i~ ~(1 ≤s_i<f_i≤N)~, lượng xăng cần di chuyển cho ~1~ (đơn vị độ dài) là ~c_i~ (đơn vị thể tích) và số lần đổ xăng tối đa là ~r_i~, xe đi từ tọa độ ~x~ đến tọa độ ~y~ sẽ mất một lượng xăng ~|x-y|×c_i~. Các xe chỉ được di chuyển theo chiều dương của trục tọa độ và chỉ có thể đổ xăng khi đến vị trí của một đại lý nào đó. Xe không thể di chuyển nếu không còn xăng. Bình chứa xăng của ~M~ chiếc xe đều có dung tích giống nhau và bằng ~V~ (đơn vị thể tích). Khi bắt đầu xuất phát, bình xăng của tất cả các xe đã đầy xăng (không tính là một lần đổ xăng), mỗi lần đổ xăng, bình xăng được đổ đầy (tức là có ~V~ (đơn vị thể tích) xăng trong bình).</p>

Yêu cầu: Hãy tính xem, giá trị ~V~ nhỏ nhất bằng bao nhiêu để với mọi chiếc xe đều có thể vận chuyển được sữa, tức là chiếc xe thứ ~i~ có thể chuyển sữa được từ đại lý ~s_i~ đến đại lý ~f_i~ với mọi ~i=1,2,3,...,M~.

Input

• Dòng ~1~ ghi ~2~ số nguyên dương ~N~ và ~M~ tương ứng là số đại lý và số xe chở sữa.
• Dòng ~2~ ghi ~N~ số nguyên dương ~x_1,x_2,…,x_N~ ~(0<x_1<x_2<⋯<x_N<10^9)~ tương ứng là tọa độ của ~N~ đại lý.</li>
• ~M~ dòng cuối, dòng thứ ~i,(i=1,2,...,M)~ ghi ~4~ số nguyên ~s_i,f_i,c_i,r_i (1 ≤s_i<f_i≤N, 1 ≤c_i≤10^9;0≤r_i≤N)~ là thông tin của chiếc xe thứ i.</li>

Output

• Một số nguyên là giá trị nhỏ nhất của ~V~ để tất cả các xe đều có thể vận chuyển được sữa.

Subtask

• Có ~25\%~ số test ứng với ~1\le N \le 10^5, M = 1~.
• Có ~25\%~ số test ứng với ~2 \le N \le 100, 2 \le M \le 10~.
• ~50~ số test còn lại ứng với ~100 < N \le 400~, ~2 \le M \le 5.10^5~

Sample Input 1

5 2
1 3 8 12 15
1 3 10 0
2 4 5 1

Sample Output 1

70

Explanation 1

• Xe ~1~, di chuyển từ đại lý ~1~ đến đại lý ~3~, tức là tọa độ ~1~ đến tọa độ ~8~. Xe không được đổ xăng lần nào, do vậy sẽ dùng xăng trong bình lúc xuất phát. Lượng xăng ít nhất cần là ~|8-1|×10=70~ . Như vậy ~V~ bằng ~70~ thì xe ~1~ có thể đi được từ đại lý ~1~ đến đại lý ~3~.
• Xe ~2~, di chuyển từ đại lý ~2~ đến đại lý ~4~, tức là tọa độ ~3~ đến tọa độ ~12~. Xe được đổ xăng thêm một lần.
  • Đi từ tọa độ ~3~ đến tọa độ ~8~ hết ~|8-3|×5=25~.
  • Đi từ tọa độ ~8~ đến tọa độ ~12~ hết ~|12-8|×5=20~.
  • Như vậy, ~V = 25~ thì xe thứ ~2~ đi từ đại lý ~2~ đến đại lý ~3~; đổ xăng tại đại lý ~3~ và đi từ đại lý ~3~ đến đại lý ~4~.

• Do vậy, giá trị ~V~ nhỏ nhất để ~2~ xe có thể vận chuyển được sữa là ~70~.

Bài giảng về quy hoạch động được minh họa bằng bài toán tìm đường đi trên lưới ô vuông như sau. Cho lưới ô vuông hình chữ nhật có ~m~ dòng và ~n~ cột. Mỗi ô ~(i,j)~ của lưới có ghi một số nguyên ~a_{ij}~, với ~(i \in [1,m], j \in [1,n])~. Từ mỗi ô chỉ có thể di chuyển sang ô kề cạnh bên phải hoặc xuống dưới (nếu tồn tại ô đến). Giá trị đường đi là tổng các số ghi trên những ô nằm trên đường đi. Hãy tìm đường đi có giá trị lớn nhất, xuất phát từ ô đầu bên trái và kết thúc ở ô dưới bên phải. Đường đi này được gọi là đường đi tối ưu.

Bài giảng trên được mở rộng và nâng cao ở buổi ngoại khóa cho học sinh giỏi. Một loạt các test được tạo ra để kiểm tra chương trình của học sinh. Xây dựng test mới là một việc khó và buồn tẻ. Vì vậy thầy giáo thông báo là sử dụng các test cũ đã có, nhưng ở mỗi test giá trị một ô bị thay đổi thành số cực nhỏ (có thể bằng ~0~ hoặc âm) để đường đi tối ưu không còn được như cũ và giá trị đường đi tối ưu mới sẽ là giá trị nhỏ nhất trong các khả năng giá trị một ô bị thay đổi. Ô trên trái và ô dưới phải vẫn giữ nguyên giá trị cũ. Hình vẽ sau minh họa cho ví dụ ở dưới.

Input

• Dòng đầu tiên chứa ~2~ số nguyên ~m~ và ~n~ ~(2 \le n,m \le 1500)~.
• Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa ~n~ số nguyên miêu tả ma trận ~a~.

Output

• Ghi ra một số nguyên dương duy nhất là giá trị đường đi tối ưu mới.

Subtask

• Có ~60\%~ số test ứng với ~2 \le m,n \le 50~.
• Có ~20\%~ số test ứng với ~2 \le n,m \le 300~.
• ~20\%~ số test còn lại không giới hạn gì thêm.

Sample Input 1

4 4
1 2 3 4
2 1 3 1
3 2 3 5
1 3 4 1

Sample Output 1

17