Cho một đồ thị gồm ~n~ đỉnh và ~m~ cạnh có hướng có trọng số.

Với mỗi đỉnh ~i~, hãy tính độ dài của quãng đường ngắn nhất để đi xuất phát từ đỉnh ~1~, đi qua đỉnh ~i~ và quay về đỉnh ~1~.

Input

• Dòng thứ nhất chứa ~2~ số nguyên dương ~n,m~.
• ~m~ dòng sau mỗi dòng gồm ~3~ số nguyên dương ~u,v,w~ ~(1 \le u, v \le n, u \neq v)~, miêu tả cạnh gồm đỉnh ~u~ nối với đỉnh ~v~ có trọng số ~w~.

Output

• Gồm ~n-1~ dòng, dòng thứ ~i~ in ra độ dài của quãng đường ngắn nhất để đi xuất phát từ đỉnh ~1~, đi qua đỉnh ~i + 1~ và quay về đỉnh ~1~. Nếu không có quãng đường nào như vậy thì in ra ~-1~.

Constraints

• ~1 \le n,n \le 2*10^5~.
• ~1 \le w \le 10^9~.

Subtasks

• Subtask ~1~: Nếu tồn tại cạnh ~(u,v,w)~ thì sẽ có cạnh ~(v,u,w)~. ~(30\%)~
• Subtask ~2~: Không có ràng buộc gì thêm ~(70\%)~

Sample Input 1:

5 7
1 4 5
1 5 3
3 5 2
5 4 10
5 1 7
3 2 5
2 1 1

Sample Output 1:

-1
-1
-1
10

Sample Input 2:

2 1
2 1 10

Sample Output 2:

-1

Có ~n~ điểm từ ~1~ tới ~n~ trên trục tọa độ ~OX~. Điểm thứ ~i~ có màu ~c_i~.

Tại điểm ~i~, bạn có thể:

• Đi tới điểm ~i+1~ (nếu ~i \neq n~), tốn ~R~ giây.
• Đi tới điểm ~i-1~ (nếu ~i \neq 1~), tốn ~L~ giây.
• Tốc biến tới điểm ~j~ (nếu ~c_i = c_j~), tốn ~C~ giây.

Cho ~2~ điểm ~st~ và ~en~, hãy tính thời gian ngắn nhất để đi từ ~st~ đến ~en~.

Input

• Dòng thứ nhất chứa ~4~ số nguyên dương ~n,L,R,C~.
• Dòng thứ hai gồm ~2~ số nguyên dương ~st~ và ~en~. ~(1 \le st \le en \le n)~
• Dòng thứ ba chứa ~N~ số nguyên dương ~c_1, c_2, ..., c_n~ là màu của từng điểm.

Output

• In ra thời gian ngắn nhất để đi từ ~st~ đến ~en~.

Constraints

• ~1 \le n \le 10^5~.
• ~1 \le L,R,C \le 10^9~.
• ~1 \le c_i \le 10^5~.

Sample Input 1:

5 1 2 3
1 5
1 2 1 1 2

Sample Output 1:

5

Sample Input 1:

5 1 4 3
3 5
1 2 1 1 2

Sample Output 1:

4

Subtasks

• Subtask ~1~: ~n \le 1000~ ~(50\%)~
• Subtask ~2~: Không có ràng buộc gì thêm ~(50\%)~

Đất nước ~ABC~ có ~n~ thành phố và ~m~ con đường hai chiều. Con đường thứ ~i~ nối hai thành phố ~u_i~ và ~v_i~ với nhau, có độ dài ~l_i~ và độ đẹp ~b_i~.

~H~ là một du khách. Hiện tại, anh đang ở thành phố ~1~ và cần đi tới thành phố ~n~ để dự sự kiện. Là một người đam mê cái đẹp, anh muốn chọn một lộ trình sao cho những con đường anh đi qua có tổng độ đẹp là lớn nhất, tuy vậy do cần tiết kiệm thời gian nên anh sẽ chỉ chọn lộ trình ngắn nhất (tức là tổng độ dài các con đường là bé nhất có thể) để đi từ ~1~ tới ~n~.

Hãy giúp ~H~ tính toán lộ trình ngắn nhất và có tổng độ đẹp lớn nhất mà anh ta có thể đi.

Input

• Dòng thứ nhất chứa ~2~ số nguyên dương ~n,m~.
• ~m~ dòng sau mỗi dòng gồm ~4~ số nguyên dương ~u_i,v_i,l_i,c_i~ ~(1 \le u, v \le n, u \neq v)~, miêu tả con đường nối thành phố ~u_i~ với ~v_i~ có độ dài ~l_i~ và độ đẹp ~c_i~.

Output

• Gồm một dòng chứa hai số nguyên ~L~ và ~B~, với ~L~ là độ dài của lộ trình ngắn nhất để đi từ ~1~ tới ~n~ và ~B~ là độ đẹp lớn nhất có thể của các lộ trình có độ dài ~L~.
• Nếu không có lộ trình nào để đi từ ~1~ tới ~n~, in ra ~-1~.

Constraints

• ~1 \le n,m \le 2*10^5~.
• ~1 \le l_i,c_i \le 10^9~.

Subtasks

• Subtask ~1~: ~1 \le n,m \le 20~ ~(30\%)~
• Subtask ~2~: Không có ràng buộc gì thêm ~(70\%)~

Sample Input 1:

5 6
1 5 8 9
1 2 3 2
2 5 3 4
1 3 1 1
3 4 1 5
4 5 4 1

Sample Output 1:

6 7

Explanation 1:

Có hai lộ trình có độ dài ~6~ có thể đi là ~(1,2,5)~ và ~(1,3,4,5)~. Trong đó lộ trình ~(1,3,4,5)~ có độ đẹp lớn nhất là bằng ~7~.

Sample Input 2:

4 2
1 2 1 1
1 3 1 1

Sample Output 2:

-1

Explanation 2:

Không có lộ trình nào để đi từ ~1~ tới ~4~.

Ở một vương quốc nọ có ~n~ thành phố, được đánh số từ ~1~ đến ~n~. Mạng lưới giao thông của vương quốc gồm ~m~ con đường, con đường thứ ~i~ nối hai thành phố ~u_i~ và ~v_i~ với độ dài đúng bằng ~1~ ki-lô-mét.

Có ~k~ dự án nhà máy điện đang được triển khai, dự án thứ ~j~ sẽ xây một nhà máy điện đặt tại thành phố ~p_j~, cung cấp điện cho tất cả các thành phố nằm trong bán kính ~r_j~ ki-lô-mét (giả sử rằng quãng đường di chuyển trong nội thành là bằng ~0~). Nhà vua đang băn khoăn, những thành phố nào đã được cấp điện, và những thành phố nào chưa được cấp điện? Hãy giúp nhà vua giải quyết bài toán này nhé.

Input

Dòng đầu chứa ba số nguyên ~n~, ~m~, ~k~ (~2 \le n, m \le 2 \times 10^5~; ~0 \le k \le 5 \times 10^5~).

~m~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~u_i~, ~v_i~ (~1 \le u_i, v_i \le n~; ~u_i \ne v_i~) mô tả con đường thứ ~i~.

~k~ dòng tiếp theo, dòng thứ ~j~ chứa hai số nguyên ~p_j~, ~r_j~ (~1 \le p_j \le n~; ~0 \le r_j \le 10^9~) mô tả dự án thứ ~j~.

Output

Gồm một dòng duy nhất chứa một xâu nhị phân gồm ~n~ kí tự, kí tự thứ ~i~ bằng "1" nếu thành phố thứ ~i~ đã được cấp điện, ngược lại kí tự thứ ~i~ bằng "0" nếu thành phố thứ ~i~ chưa được cấp điện.

Scoring

• Subtask ~1~ (~40\%~ số điểm): ~n, m \le 1000~.
• Subtask ~2~ (~30\%~ số điểm): ~r_1 = r_2 = \dots = r_{k - 1} = r_k~.
• Subtask ~3~ (~30\%~ số điểm): Không có ràng buộc gì thêm.

Example

Input 1

4 3 1
1 2
1 3
2 4
2 1

Output 1

1101

Input 2

6 8 2
1 3
1 5
1 6
2 5
2 6
3 4
3 5
5 6
6 0
3 1

Output 2

101111

Software and cathedrals are much the same – first we build them, then we pray 😈

Dưới lòng đất của HNA là hệ thống đường ngầm dày đặc gồm ~n~ địa điểm đánh số từ ~1~ đến ~n~. Có ~m~ đoạn đường ngầm, đoạn đường ngầm thứ ~i~ kết nối địa điểm ~u_i~ và ~v_i~ có chi phí là ~c_i~, nghĩa là muốn kích hoạt sử dụng đoạn đường hầm này phải trả chi phí là ~c_i~. LetterC67 và ~aúR là đôi bạn thân đang hoạt động dưới lòng đất này.

Buổi sáng, LetterC67 cần đi từ ~A~ đến ~B~, và tất nhiên cậu chọn tuyến đường sao cho cần trả ít chi phí nhất.

Buổi chiều, ~aúR cần đi từ ~C~ đến ~D~, nhưng may thay, những đoạn đường hầm mà buổi sáng LetterC67 đã trả chi phí để kích hoạt rồi thì ~aúR có thể sử dụng mà không cần trả chi phí nữa.

Hãy hãy tính xem ~aúR cần trả chi phí ít nhất là bao nhiêu?

Input: tunnel.inp

• Dòng đầu tiên gồm hai số nguyên ~n, m~.
• Dòng thứ hai là bốn số nguyên ~A, B, C, D~.
• ~m~ dòng tiếp theo, mỗi dòng gồm ba số nguyên ~u_i, v_i, c_i~.
• Dữ liệu đảm bảo từ một địa điểm có thể đi đến mọi địa điểm khác, không có hai đoạn đường hầm nối cùng một cặp địa điểm.

Output: tunnel.out

• In ra một số nguyên là kết quả của bài toán.

Note

• Trong mọi test: ~A \neq B, C \neq D~, ~1 \le u_i < v_i \le n~, ~1 \le c_i \le 10^9~.
• Subtask 1 (~15\%~ số điểm): ~A=C~;
• Subtask 2 (~15\%~ số điểm): Có duy nhất một tuyến đường từ ~A~ đến ~B~ có giá trị nhỏ nhất;
• Subtask 3 (~30\%~ số điểm): ~n \le 300~;
• Subtask 4 (~40\%~ số điểm): ~2 \le n \le 10^5, 1 \le m \le 2 \times 10^5~

Ví dụ

Input:

6 6
1 6 1 4
1 2 5
2 3 1
3 5 1
2 4 3
4 5 2
5 6 1

Output:

2

Giải thích:

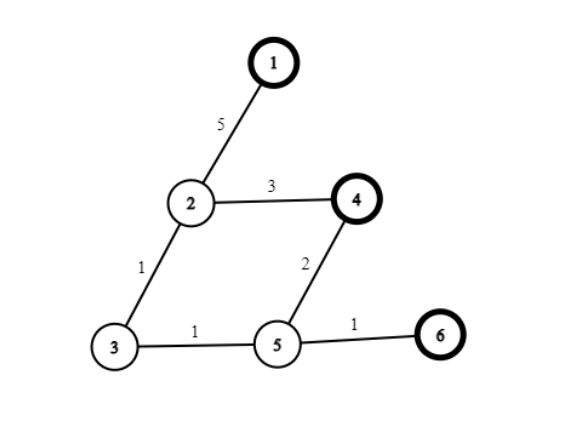
• Chỉ có duy nhất một đường đi ngắn nhất từ ~1~ đến ~6~ là ~1-2-3-5-6~, nên LetterC67 sẽ sử dụng tuyến đường này.
• ~aúR sẽ chỉ phải trả chi phí thêm đoạn đường hầm ~4-5~ với giá trị ~2~ đến di chuyển từ ~1~ đến ~4~.

Châu đang muốn quảng bá dòng xe điện Cessla của mình bằng cách giới thiệu mạng lưới các trạm sạc của Cessla. Anh ấy đã xác định được ~N (2 \le N \le 5*10^4)~ điểm quan tâm được đánh số từ ~1~ đến ~N~, trong đó ~C(1 \le C \le N)~ trạm đầu tiên là các trạm sạc và còn lại là các điểm du lịch. Các điểm này được kết nối với nhau bởi ~M(1\le M \le 10^5)~ đường hai chiều, đường thứ ~i~ nối hai điểm phân biệt ~u_i~ và ~v_i~ và có độ dài ~l_i~ dặm ~(1\le l_i \le 10^9)~.

Cessla có thể di chuyển với quãng đường lên tới ~2R~ dặm ~(1 \le R \le 10^9)~ trong một lần sạc, cho phép nó đến bất kỳ điểm đến nào trong phạm vi ~R~ dặm tính từ trạm sạc. Một điểm đến được coi là kết nối tốt nếu có thể đến được điểm đến đó từ ít nhất ~K(1\le K\le 10)~ trạm sạc riêng biệt. Nhiệm vụ của bạn là hỗ trợ John xác định các điểm đến du lịch có kết nối tốt.

Input

Dòng đầu tiên chứa năm số nguyên ~N,M,C,R,K~. Mỗi dòng trong ~M~ dòng tiếp chứa ba số nguyên cách nhau bằng dấu cách ~u_i,v_i,l_i~ sao cho ~u_i \ne v_i~. Các trạm sạc được đánh số ~1,2,...,C~. Các điểm còn lại đều là các điểm du lịch.

Output

Đầu tiên, in ra số lượng điểm đến du lịch có kết nối tốt trên một dòng. Sau đó, liệt kê tất cả các điểm đến du lịch có kết nối tốt theo thứ tự tăng dần, mỗi điểm trên một dòng riêng biệt.

Scoring

• Subtask ~1~: ~K=2~, ~N \le 500~ và ~M \le 1000~.
• Subtast ~2~: ~K=2~.
• Subtask ~3~: Không có điều kiện gì thêm.

Example

Sample Input 1

3 3 1 4 1
1 2 3
1 3 5
2 3 2

Sample Output 1

1
2

Explanation

Chúng ta có một trạm sạc ở ~1~. Từ trạm sạc này, chúng ta có thể đến điểm ~2~ (vì nó cách ~1~ khoảng cách là ~3~), nhưng không thể đến điểm ~3~ (vì nó cách ~1~ khoảng cách là ~5~). Như vậy chỉ có điểm ~2~ là kết nối tốt.

Sample Input 1

4 3 2 101 2
1 2 1
2 3 100
1 4 10

Sample Output 1

2
3
4

Explanation

Chúng ta có các trạm sạc tại ~1~ và ~2~, và cả hai điểm ~3~ và ~4~ đều cách hai điểm ~1~ và ~2~ khoảng cách là ~101~. Vì vậy, cả hai điểm ~3~ và ~4~ đều có kết nối tốt.

Có ~n~ loại đồ vật, mỗi loại có giá ~a[i]~ và số lượng tối đa ~cnt[i]~.

Bạn cần tìm cách mua hàng nhỏ thứ ~K~, trong đó:

• Một cách mua hàng là một bộ ~b[1], b[2], ..., b[n]~, với ~0 \leq b[i] \leq cnt[i]~.
• Tổng chi phí của một cách mua hàng là: ~sum_{i=1}^{n} a[i] \times b[i]~
• Bạn sắp xếp tất cả các cách mua hàng theo chi phí tăng dần và chọn cách có chi phí nhỏ thứ ~K~.

Input

• Dòng đầu chứa hai số nguyên dương ~n, k~ (~n, k \leq 2 \times 10^{5}~).
• ~n~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~a[i], cnt[i]~ (~a[i] \leq 10^9, cnt[i] \leq 2 \times 10^{5}~).

Output

• In ra chi phí của cách mua hàng nhỏ thứ ~K~.

Scoring

• Subtask 1 (20% số điểm): ~n \leq 20~.
• Subtask 2 (20% số điểm): ~n \leq 100, a[i], b[i] \leq 100~.
• Subtask 3 (20% số điểm): ~cnt[i] = 1~.
• Subtask 4 (40% số điểm): Không có ràng buộc gì thêm.

Example

Test 1

Input

3 5
2 3
1 2
3 1

Output

3

Note

• Các cách mua hàng hợp lệ có chi phí sắp xếp tăng dần:

  • 0: Không mua gì.
  • 1: Mua 1 món loại 2 (giá 1).
  • 2: Mua 2 món loại 2 (giá 2).
  • 2: Mua 1 món loại 1 (giá 2).
  • 3: Mua 3 món loại 2 (giá 3).
  • 3: Mua 2 món loại 1 (giá 3).
  • 4: Mua 1 món loại 1 và 1 món loại 2 (giá 4).

• Cách mua nhỏ thứ 5 có chi phí 3.