Cho đồ thị đầy đủ vô hướng có trọng số (nghĩa là đồ thị gồm ~\frac{n*(n-1)}{2}~ cạnh phân biệt), trong đó có ~m~ cạnh có trọng số là ~1~, các cạnh còn lại có trọng số là ~0~.

Hãy tìm cây khung nhỏ nhất của đồ thị này.

Input:

• Dòng đầu tiên ghi số nguyên ~n~ và ~m~ ~(1 \le n \le 2*10^5, 1 \le m \le min(4*10^5,\frac{n*(n-1)}{2}))~
• ~m~ dòng tiếp theo, mỗi dòng gồm ~2~ số nguyên ~u_i,v_i~ ~(1 \le u_i, v_i \le n, u_i \neq v_i)~ - miêu tả cạnh ~(u_i,v_i)~ có trọng số là ~1~.

Output:

• Trọng số của cây khung nhỏ nhất của đồ thị.

Constraints:

• Có ~50\%~ số test ứng với ~n \le 2*10^3~
• ~50\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input 1

6 11
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6

Output 1

2

Input 2

3 0

Output 2

0

Cho đồ thị vô hướng có trọng số gồm ~n~ đỉnh, đồng thời có thêm ~m~ truy vấn có một trong hai dạng như sau:

• ~1~ ~u~ ~v~ thêm cạnh ~(u,v)~ vào đồ thị.
• ~2~ ~u~ ~v~ in ra thời gian sớm nhất (chỉ số của truy vấn) để ~u~ và ~v~ liên thông.

Input:

• Dòng đầu tiên ghi số nguyên ~n~ và ~m~ ~(1 \le n \le 2*10^5; 1 \le m \le 5*10^5)~
• ~m~ dòng tiếp theo, mỗi dòng gồm ~3~ số nguyên ~t,u,v~, nếu ~t = 1~ thì là dạng truy vấn thứ nhất, ngược lại là dạng thứ hai.

Output:

• Với mỗi truy vấn loại ~2~, in ra kết quả. Nếu hai đỉnh chưa liên thông, in ra ~-1~.

Constraints:

• Có ~50\%~ số test ứng với ~n,m \le 2*10^3~;
• ~50\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input

4 5
1 1 2
2 1 2
1 2 3
2 1 3
2 1 4

Output

1
3
-1

Một đế chế đang xây dựng mạng lưới cho các hành tinh trong nó. Đế chế gồm có ~N~ hành tinh được biểu diễn như các điểm trong không gian 3 chiều. Chi phí phải chi cho việc nối giữa hành tinh ~A~ và hành tinh ~B~ là ~min~{ |~x_A - x_B~|, |~y_A - y_B~|, |~z_A~ - ~z_B~| } với (~x_A~, ~y_A~, ~z_A~), (~x_B~, ~y_B~, ~z_B~) là tọa độ của hành tinh ~A~, ~B~ trong không gian 3 chiều.

Đế chế dự tính sẽ xây dựng ~N – 1~ cầu nối như vậy để các hành tinh liên thông với nhau và chi phí để trả sao cho phải nhỏ nhất có thể.

Input

• Dòng đầu là số hành tinh ~N~.
• N dòng sau mỗi dòng là tọa độ của một hành tinh.

Output

• Ghi trên một dòng duy nhất chi phí nhỏ nhất có thể.

Sample Input 1

5
11 -15 -15
14 -5 -15
-1 -1 -5
10 -4 -1
19 -4 19

Sample Output 1

4

Cho đồ thị vô hướng có trọng số gồm ~n~ đỉnh và ~m~ cạnh không chứa khuyên.

Với mỗi cạnh ~(u,v)~ được cho, hãy tìm trọng số nhỏ nhất có thể của cây khung chứa cạnh ~(u,v)~. Nói cách khác, ta cần tìm trọng số của cây khung nhỏ nhất chứa cạnh ~(u,v)~.

Trọng số cây khung bằng tổng trọng số của tất cả các cạnh trong cây khung.

Input:

• Dòng đầu tiên ghi số nguyên ~n~ và ~m~ ~(1 \le n \le 2*10^5, n-1 \le m \le 2*10^5)~
• ~m~ dòng tiếp theo, mỗi dòng gồm ~3~ số nguyên ~u_i,v_i,w_i~ ~(1 \le u_i, v_i \le n, u_i \neq v_i, 1 \le w_i \le 10^9)~ - lần lượt là hai đỉnh và trọng số của cạnh thứ ~i~.

Output:

• In ra ~m~ dòng, dòng thứ ~i~ chứa trọng số cạnh của cây khung thứ ~i~.

Constraints:

• Có ~50\%~ số test ứng với ~n,m \le 2*10^3~;
• ~50\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input

5 7
1 2 3
1 3 1
1 4 5
2 3 2
2 5 3
3 4 2
4 5 4

Output

9
8
11
8
8
8
9

Cho đồ thị vô hướng có trọng số gồm ~n~ đỉnh và ~m~ cạnh không chứa khuyên, mỗi cạnh có dạng ~(u,v,c)~, tức là cạnh nối hai đỉnh ~u~ và ~v~ có trọng số ~c~. Lưu ý, không tồn tại quá 5 cạnh có cùng trọng số là ~c~.

Hãy đếm số cây khung nhỏ nhất của đồ thị này. Nói cách khác, đếm số cách giữ lại ít cạnh nhất của đồ thị sao cho đồ thị vẫn liên thông và tổng trọng số các cạnh giữ lại là nhỏ nhất.

Do kết quả có thể rất lớn, hãy in ra đáp số theo modulo ~998244353~.

Input:

• Dòng đầu tiên ghi số nguyên ~n~ và ~m~ ~(1 \le n \le 2*10^5, n-1 \le m \le 2*10^5)~
• ~m~ dòng tiếp theo, mỗi dòng gồm ~3~ số nguyên ~u_i,v_i,w_i~ ~(1 \le u_i, v_i \le n, u_i \neq v_i, 1 \le w_i \le 10^9)~ - lần lượt là hai đỉnh và trọng số của cạnh thứ ~i~.
• Dữ liệu đảm bảo đồ thị liên thông.

Output:

• Gồm một số nguyên duy nhất là số cây khung nhỏ nhất của đồ thị modulo ~998244353~.

Constraints:

• Có ~10\%~ số test ứng với ~m \le 7~
• Có ~20\%~ số test ứng với ~m \le 25~
• Có ~30\%~ số test ứng với ~n = m~;
• ~40\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input 1

3 3
1 2 1
2 3 1
3 1 1

Output 1

3

Input 2

4 6
1 2 1
3 4 1
1 3 2
2 4 2
1 4 3
2 3 3

Output 2

2

Input 3

4 9
1 2 1
1 2 1
2 3 2
2 3 2
2 3 2
3 4 3
3 4 3
3 4 3
3 4 3

Output 3

24

Cho đồ thị vô hướng có trọng số gồm ~n~ đỉnh và ~m~ cạnh không chứa khuyên, mỗi cạnh có dạng ~(u,v,c)~, tức là cạnh nối hai đỉnh ~u~ và ~v~ có trọng số ~c~.

Với mỗi cạnh, hãy xác định xem cạnh đó có nằm trong mọi cây khung nhỏ nhất của đồ thị hay không.

Input:

• Dòng đầu tiên ghi số nguyên ~n~ và ~m~ ~(1 \le n \le 2*10^5, n-1 \le m \le 2*10^5)~
• ~m~ dòng tiếp theo, mỗi dòng gồm ~3~ số nguyên ~u_i,v_i,w_i~ ~(1 \le u_i, v_i \le n, u_i \neq v_i, 1 \le w_i \le 10^9)~ - lần lượt là hai đỉnh và trọng số của cạnh thứ ~i~.
• Dữ liệu đảm bảo đồ thị liên thông.

Output:

• In ra ~m~ xâu kí tự, trong đó xâu thứ ~i~ là "Yes" nếu cạnh thứ ~i~ thuộc toàn bộ các cây khung nhỏ nhất của đồ thị, "No" nếu ngược lại.

Constraints:

• Có ~10\%~ số test ứng với ~m \le 20~
• Có ~20\%~ số test ứng với ~m \le 300~
• Có ~20\%~ số test ứng với ~m \le 4000~;
• Có ~20\%~ số test ứng với trọng số của mọi cạnh phân biệt.
• ~30\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input 1

5 7
4 3 2
1 2 2
1 4 7
2 5 1
1 3 9
2 4 9
2 3 7

Output 1

Yes Yes No Yes No No No 

Cho một đơn đồ thị liên thông, vô hướng, có trọng số gồm:

• ~N~ đỉnh - được đánh số từ ~1~ đến ~N~;
• ~M~ cạnh - cạnh ~(u, v, c)~ mô tả đường đi hai chiều trực tiếp giữa hai đỉnh ~u~ và đỉnh ~v~, có chi phí là ~c~;
• ~K~ đỉnh đặc biệt, phân biệt có tính chất như sau: trên đường đi, khi ở một đỉnh đặc biệt có thể di chuyển đến một đỉnh đặc biết bất kỳ trước đó đã đi qua mà không mất chi phí.

Tìm đường đi có tổng chi phí nhỏ nhất đi qua toàn bộ các đỉnh đặc biệt (đường đi có thể xuất phát từ một đỉnh bất kì).

Dữ liệu vào từ tệp văn bản DDDB.INP:

• Dòng đầu tiên gồm ba số nguyên dương ~N, M~ và ~K \ (2\le K\le N; \ N, M\le 10^5)~ mô tả số lượng đỉnh, số lượng cạnh và số lượng đỉnh đặc biệt;
• Dòng thứ hai gồm ~K~ số nguyên dương ~S \ (S \le N)~ mô tả các đỉnh đặc biệt;
• ~M~ dòng sau, mỗi dòng gồm ba số nguyên dương ~u, v, c \ (u, v\le N; \ c\le 10^9)~ mô tả các cạnh của đồ thị.

Kết quả ghi ra tệp văn bản DDDB.OUT:

Một số nguyên duy nhất là tổng chi phí nhỏ nhất của đường đi thoả mãn yêu cầu.

Ví dụ

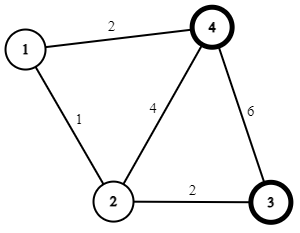
Input

4 5 2
4 3
1 2 1
2 3 2
4 1 2
4 2 4
3 4 6

Output

5

Giải thích

Có thể đi theo đường đi: ~4 \rightarrow 1 \rightarrow 2 \rightarrow 3~

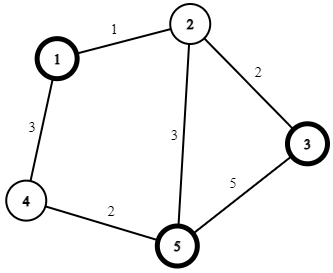
Input

5 6 3
5 1 3
1 2 1
2 3 2
4 1 3
4 5 2
5 2 3
3 5 5

Output

7

Giải thích

Có thể đi theo đường đi: ~1 \rightarrow 2 \rightarrow 3 \rightarrow 1\rightarrow 2\rightarrow 5~

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm thoả mãn: ~K=2; \ N\le 10^4~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~K=5; \ N\le 10^4~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~K=N~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~N, M\le 10^3~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~M=N-1~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm không có ràng buộc gì thêm.

Loại xe điện Alset mới được nghiên cứu bởi giáo sư Q của trường đại học LQD được đánh giá cao trong giới chuyên môn, và sẽ sớm được đưa ra thị trường. Nhằm đánh giá kĩ hơn các đặc tính của xe, các nhà đầu tư muốn theo dõi giáo sư Y mô phỏng quá trình vận hành của nó. Trong điều kiện mô phỏng, bản đồ thành phố được đơn giản hóa thành lưới ô vuông vô tận. Ta gắn vào bản đồ này một hệ trục tọa độ Oxy. Giả sử có giao lộ nằm tại mọi điểm có tọa độ nguyên của mặt phẳng; và với mọi giao lộ ~(x, y)~, luôn có con đường nối:

• Giao lộ tại ~(x, y)~ với giao lộ tại ~(x, y + 1)~.
• Giao lộ tại ~(x, y)~ với giao lộ tại ~(x + 1, y)~.

Xe điện Alset chỉ có thể đi dọc theo các con đường, đi từ một giao lộ này tới giao lộ khác liền kề nó. Trong một đơn vị thời gian, sử dụng một đơn vị năng lượng tiêu chuẩn, xe có thể đi từ giao lộ ~(x, y)~ tới giao lộ ~(u, v)~ nếu ~|x - u| + |y - v| = 1~.

Người ta cũng bố trí ~n~ trạm sạc đặc biệt, trạm thứ ~i~ ở tại giao lộ ~(x_{i}, y_{i})~. Mỗi khi dừng tại một trong những trạm này, xe sẽ được nạp đầy năng lượng, bằng với dung tích ~w~ của nó.

Trong mô phỏng này, có ~q~ thử thách được đặt ra. Thử thách thứ ~j~ giả sử rằng nếu xe bắt đầu tại trạm sạc thứ ~s_{j}~, để đi tới được trạm thứ ~t_{j}~, thì dung tích ~w~ của nó nhỏ nhất có thể bằng bao nhiêu? (trong quá trình di chuyển có thể đi qua các trạm sạc khác tùy ý).

Input

• Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ ~(1 \leq n, q \leq 2 \times 10^{5})~ lần lượt là số trạm sạc và số thử thách.
• Trong ~n~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~x_{i}~ và ~y_{i}~ ~(|x_{i}|, |y_{i}| \leq 10^{9})~ là vị trí của trạm sạc thứ ~i~.
• Trong ~q~ dòng tiếp theo, dòng thứ ~j~ chứa hai số nguyên ~s_{j}~ và ~t_{j}~ ~(1 \leq s_{j}, t_{j} \leq n)~ mô tả một thử thách thứ ~j~.

Output

• Gồm ~q~ dòng, dòng thứ ~j~ chứa đáp án của thử thách thứ ~j~.

Scoring

• Subtask ~1~ (~20\%~ số điểm): ~n, q \leq 100~.
• Subtask ~2~ (~20\%~ số điểm): ~n, q \leq 1000~.
• Subtask ~3~ (~20\%~ số điểm): ~x_{i} = 0~ với mọi ~1 \leq i \leq n~.
• Subtask ~4~ (~20\%~ số điểm): ~0 \leq x_{i} \leq 1~ với mọi ~1 \leq i \leq n~.
• Subtask ~5~ (~20\%~ số điểm): Không có ràng buộc gì thêm.

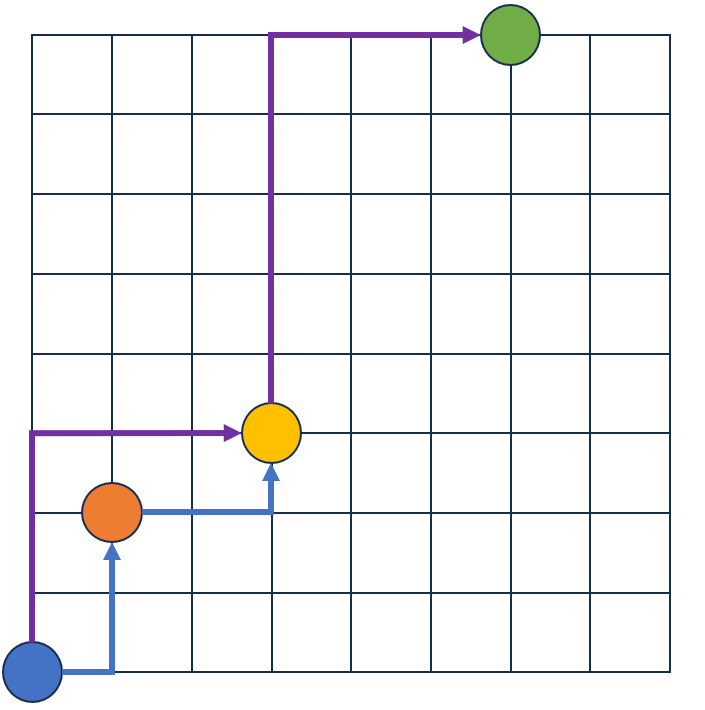
Sample Input 1

5 3
0 0
0 0
3 3
1 2
6 8
1 2
2 3
1 5

Sample Output 1

0
3
8

Explanation

Truy vấn thứ nhất, hai trạm sạc ở cùng vị trí nên dung tích nhỏ nhất sẽ là ~0~

Truy vấn thứ hai, ta có thể di chuyển như các mũi tên màu xanh dương.

Truy vấn thứ ba, ta có thể di chuyển như các mũi tên màu tìm.