Ngoài việc học và thi, Nam cũng có dự định khi đến Hạ Long nhất định phải đi quần thể vui chơi giải trí nổi tiếng là Sun World Ha Long Park.

Sun World Ha Long Park có ~n~ trò chơi trong đó có ~m~ trò chơi mạo hiểm (~m\le n~). Mỗi trò chơi được bố trí ở một địa điểm và có ~n-1~ con đường, mỗi con đường nối chính xác hai địa điểm tổ chức trò chơi. Đảm bảo tất cả các địa điểm đều được kết nối bởi các con đường này. Mỗi con đường Nam mất một phút để đi qua nó.

Vì là người ưa mạo hiểm nên Nam chỉ chơi những trò mạo hiểm mà thôi, với lại, Nam không có nhiều thời gian nên Nam nhờ các bạn xác định tổng thời gian nhỏ nhất Nam đi trên các con đường để đến tất cả các điểm tổ chức trò chơi mạo hiểm.

Input

• Dòng 1 chứa hai số nguyên ~n, m~ (~2\le m\le n\le 10^5~)
• Dòng 2 chứa ~m~ số nguyên khác nhau là số hiệu điểm tổ chức trò chơi mạo hiểm.
• ~n-1~ dòng tiếp theo, mỗi dòng hai số nguyên ~a, b~ (~0\le a,b\le n-1~) mô tả một con đường nối điểm tổ chức trò chơi có số hiệu ~a~ và ~b~.

Output

• Đưa ra một số nguyên duy nhất là tổng thời gian ít nhất Nam đi qua các con đường để đến tất cả các điểm tổ chức trò chơi mạo hiểm.

Scoring

• Subtask ~1~ (~30\%~ số điểm): ~m=2~ và ~n\le 100~
• Subtask ~2~ (~30\%~ số điểm): ~m\le n\le 10^4~
• Subtask ~3~ (~40\%~ số điểm): ~n\le 10^5~

Sample Input 1

7 2
5 0
4 0
3 1
0 6
0 1
2 1
5 2

Sample Output 1

3

Vì Gojo Satoru quá yếu, nên một ngày đẹp trời Sukuna đã rủ Chau solo bành trướng lãnh địa.

Cả ~2~ solo trên mảnh đất là một bảng hình chữ nhật ~A~, có diện tích ~N \times M~ với ~N~ hàng và ~M~ cột. Kí hiệu ~(i, j)~ là ô nằm trên hàng thứ ~i~, cột thứ ~j~ với các hàng được đánh số từ trên xuống dưới theo thự từ ~1~ đến ~N~, các cột được đánh số từ trái sang phải theo thự từ ~1~ đến ~M~.

Sukuna và Chau đã bành trướng lên lãnh địa này và vẽ ra ~2~ vùng lãnh địa của mình. Trên bảng ~A~, ta kí hiệu ~A (i , j) = 1~ nếu ô đó chứa biên của phần lãnh địa Chau, ~A (i, j) = 2~ nếu ô đó chứa biên của phần lãnh địa của Sukuna, ~A (i, j) = 3~ nếu nó chứa biên của phần lãnh địa của cả hai người, còn ~A (i, j) = 0~ nếu nó là đất trống. Đảm bảo biên của mỗi lãnh địa tạo thành một vòng khép kín. (Biên tức là vòng ngoài của lãnh địa).

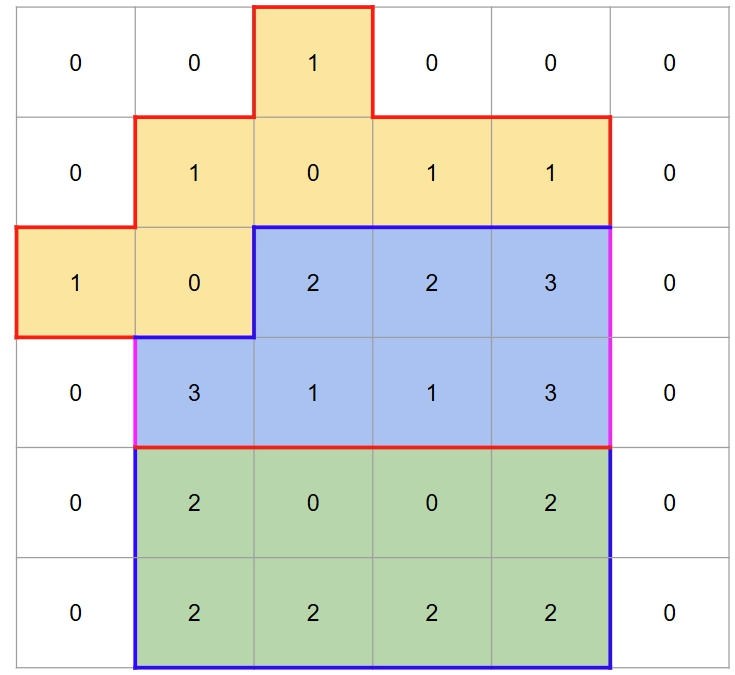
Hình trên là minh họa cho test ví dụ 1.

• Viền màu đỏ là biên của lãnh địa của Chau. Viền màu xanh là biên lãnh địa của Sukuna. Viền màu tím là biên lãnh địa của cả 2.
• Các ô màu cam là các ô thuộc chỉ thuộc lãnh địa của Chau. Các ô màu xanh lá là các ô chỉ thuộc lãnh địa của Sukuna. Các ô màu xanh dương là các ô thuộc lãnh địa của cả hai.

Vì mải dùng Thuật Thức nên Chau không thể dùng Thuật Toán, Chau muốn các bạn tính hộ xem có bao nhiêu ô thuộc cả ~2~ lãnh địa

Yêu cầu: In ra số ô thuộc cả ~2~ lãnh địa.

Input

• Dòng đầu tiên là 2 số tự nhiên ~N, M~ ~(N, M\leq 1000)~ là số hàng và cột của bảng ~A~.
• ~N~ dòng tiếp theo, môi dòng là một hàng của bảng ~A~ và có ~M~ số nguyên không âm nhỏ hơn hoặc bằng 3. Ý nghĩa giá trị của mỗi số nguyên không âm đã nếu ở đề bài ở trên.

Output

• In ra một số nguyên không âm là kết quả của bài toán.

Subtask

• Subtask ~1~ (~25\%~ số điểm): ~N = 1~ .
• Subtask ~2~ (~25\%~ số điểm): ~N, M\leq 100~ và các ô biên của 2 lãnh địa trùng nhau.
• Subtask ~3~ (~25\%~ số điểm): ~N, M\leq 100~.
• Subtask ~4~ (~25\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

6 6
0 0 1 0 0 0
0 1 0 1 1 0
1 0 2 2 3 0
0 3 1 1 3 0
0 2 0 0 2 0
0 2 2 2 2 0

Sample Output 1

7

Cho ma trận vuông ~n \times n~, các hàng được đánh số từ ~1~ tới ~n~, các cột được đánh số từ ~1~ tới ~n~. Các ô được sắp xếp theo thứ tự từ trái sang phải, từ trên xuống dưới, ô ~(i,j)~ có giá trị là ~a_{i,j}~.

Ivan Tèo đang đứng ở ô ~(1,1)~ của ma trận, trong mỗi lần đi, cậu chỉ có thể đi sang phải hoặc xuống dưới, nói cách khác, nếu đang ở ô ~(i,j)~, cậu chỉ có thể đi sang ô ~(i+1,j)~ hoặc ~(i,j+1)~. Gọi ~Best(i,j)~ là giá trị lớn nhất có thể nếu Ivan Tèo đi từ ô ~(1,1)~ tới ô ~(i,j)~. Vì cảm thấy rằng nếu chỉ hỏi các ~Best(i,j)~ thì quả là nhàm chán và không đánh giá đúng được tiềm năng của Tèo, ~mrhee~ quyết định tạo ra một giá trị mới như sau:

• Gọi ~S~ là tổng các ~Best(i,j)~ của mọi ô ~(i,j)~ trên ma trận.
• Nói cách khác, ~S = \sum Best(i,j)~, với mọi ~(1 \le i,j \le n)~.

Vì lại cảm thấy việc in ra ~S~ của ma trận hiện tại là quá dễ với Tèo, ~mrhee~ quyết định tạo ra ~q~ sự thay đổi, sự thay đổi thứ ~i~ có dạng như sau:

• Cho ba số nguyên ~u_i,v_i,delta_i~ ~(1 \le u_i,v_i \le n, -1\le delta_i \le 1)~, tức gán giá trị ~a_{u_i,v_i} = a_{u_i,v_i} + delta_i~.
• Sau mỗi truy vấn, hãy in ra giá trị ~S~ của ma trận mới.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~n,q~ ~(1 \le n \le 1000, 1 \le q \le 3 \times 10^4)~
• ~n~ dòng sau, dòng thứ ~i~ gồm ~n~ số nguyên, số thứ ~j~ miêu tả giá trị ~a_{i,j}~ ~(-10^2 \le a_{i,j} \le 10^2)~ của ma trận.
• ~q~ dòng tiếp theo, mỗi dòng gồm ba số nguyên ~u_i,v_i,delta_i~ ~(1 \le u_i,v_i \le n, -1 \le delta_i \le 1)~ miêu tả truy vấn thứ ~i~.

Output:

• Gồm một dòng in ra số cặp ~(i,j)~ thỏa mãn.

Subtask:

• Subtask ~1~ (~25\%~ số điểm): ~q \le 10~.
• Subtask ~2~ (~25\%~ số điểm): Ô ~(u_i,v_i)~ trong mọi truy vấn là giống nhau và ~q \le 3000~, đồng thời ~delta_i = 1~ với mọi truy vấn.
• Subtask ~3~ (~30\%~ số điểm): ~q \le 3000~
• Subtask ~4~ (~20\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

2 2
1 2
2 2
1 2 0
2 1 1

Sample Output 1

12
14

Sample Input 2

4 4
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
1 1 1
2 2 -1
3 1 1
1 3 -1

Sample Output 2

196
195
203
199

Explanation

Ở ví dụ ~1~, sau truy vấn đầu, bảng không thay đổi gì, ta có các ~Best(i,j)~ như sau:

• ~Best(1,1) = 1~
• ~Best(1,2) = 3~
• ~Best(2,1) = 3~
• ~Best(2,2) = 5~

Sau khi tăng ô ~(2,1)~ lên ~4~ đơn vị, ta có:

• ~Best(1,1) = 1~
• ~Best(1,2) = 3~
• ~Best(2,1) = 4~
• ~Best(2,2) = 6~