Cho hàm ~f(x)~ nhận đầu vào ~x~ là số nguyên không âm được định nghĩa như sau:

• Nếu ~x<10, f(x)=x~
• Ngược lại ~f(x)=f(D(x))~ với ~D(x)~ là tổng các chữ số trong biểu diễn thập phân của ~x~.
• Cho số nguyên dương ~n~, hãy tính ~f(n)~ .

Input:

Gồm một dòng duy nhất chứa số nguyên n ~(1≤n<10^{100000}).~

Output:

In ra một số nguyên là kết quả.

Sample Input 1

4

Sample Output 1

4

Số đẹp được định nghĩa là một số nguyên dương và chia hết cho một trong hai số: ~3~ hoặc ~5~.

Ví dụ về dãy các số đẹp: ~3, 5, 6, 9, 10, 12, 15, 18, 20,...~

Hãy tìm số đẹp thứ ~k~.

Input

• Gồm một dòng chứa số nguyên dương ~k~.

Output

• In ra kết quả của bài toán.

Giới hạn:

• Subtask 1 (~50\%~ số điểm): ~k \le 10^6~
• Subtask 2 (~50\%~ số điểm): ~k \le 10^{12}~

Sample Input 1

2

Sample Output 1

5

Sample Input 2

10

Sample Output 2

21

Bạn được nhận ~n~ xâu kí tự, mỗi xâu gồm các chữ cái tiếng Anh in thường. Cần chọn ra một số xâu trong ~n~ xâu đó sao cho khi ghép tất cả chúng lại, ta được một xâu mới bao gồm đầy đủ các kí tự trong bảng chữ cái tiếng Anh. Hãy đếm số cách để thực hiện yêu cầu trên. Hai cách được coi là khác nhau khi có một xâu được chọn ở cách này không được chọn trong cách kia.

Input

• Dòng đầu tiên gồm số nguyên dương ~n~ ~(n \le 25)~ miêu tả số lượng xâu.
• ~n~ dòng tiếp theo, mỗi dòng bao gồm một xâu kí tự ~S~ ~(|S| \le 30)~ gồm các chữ cái tiếng Anh in thường.

Output

• In ra một số nguyên là kết quả bài toán.

Sample Test

Input1:

8
the
quick
brown
fox
jumps
over
lazy
dog

Output1:

1

Input2:

3
a
b
abcdefghijklmnopqrstuvwxyz

Output2:

4

Cho hai dãy ~a~ và ~b~ cùng có ~n~ phần tử nguyên. Ta định nghĩa hàm ~sum(x,y)~ ~(1 \le x,y \le n)~ như sau:

• Nếu ~x \le y~ thì ~sum(x,y) = a_x + a_{x+1} + a_{x+2} + ... + a_y~.
• Nếu ~x > y~ thì ~sum(x,y) = b_x + b_{x-1} + b_{x-2} + ... + b_y~.

Nhiệm vụ của bạn là, hãy chọn ra hai đoạn ~[x,y]~ ~(1 \le x \le y \le n)~ và ~[c,d]~ ~(1 \le c \le d \le n)~ sao cho ~S = \sum sum(i,j)~ với mọi ~x \le i \le y~ và ~c \le j \le d~ là lớn nhất.

Constraint

• ~1 \le n \le 400~.
• ~-10^6 \le b_i, a_i \le 10^6~.

Input

• Dòng đầu gồm số nguyên dương ~n~.
• Dòng thứ hai gồm ~n~ số nguyên miêu tả dãy ~a~.
• Dòng thứ ba gồm ~n~ số nguyên miêu tả dãy ~b~.

Output

• In ra ~S~ lớn nhất tìm được.

Subtask

• ~30\%~ số test có ~n \le 10~
• ~40\%~ số test có ~n \le 50~.
• ~30\%~ số test có ~n \le 400~.

Sample Input 1

5
1 4 2 -1 -2
-2 -1 1 2 -1

Sample Output 1

45

Explanation 1

• Chọn đoạn ~[1,5]~ và ~[2,5]~.

There are 10 types of people in this world. Those who understand binary and those who don't 😈

Hôm nay là ngày nghỉ của Ti36, điều đó có nghĩa là sẽ không có gì ngăn cản anh ấy làm điều mình yêu thích - xem phim truyền hình dài tập. Trong suốt cả ngày, kênh A sẽ chiếu phần mới nhất của loạt phim "Avengers" và kênh B sẽ chiếu phần mới nhất của loạt phim "Batman".

Vì Ti36 không muốn chỉ xem một bộ phim duy nhất trong hai bộ phim này nên anh ấy quyết định xem cả hai, anh ấy sẽ chuyển sang kênh khác để xem phim còn lại mỗi khi quảng cáo bắt đầu ở kênh anh ấy đang xem. Vào thời điểm ~0~, Ti36 sẽ bật TV và bắt đầu xem loạt phim "Avengers" trên kênh A. Nếu bất cứ lúc nào trên kênh truyền hình mà Ti36 đang xem có quảng cáo bắt đầu, thì Ti36 sẽ chuyển sang kênh kia và xem kênh đó. Nếu Ti36 chuyển kênh và cũng có một quảng cáo đang diễn ra vào lúc này, thì anh ấy sẽ không chuyển kênh với hy vọng rằng quảng cáo sẽ sớm kết thúc trên kênh này. Vào thời điểm ~t~, Ti36 sẽ tắt TV và đi ngủ.

Cho biết lịch chiều quảng cáo cụ thể và thời lượng của các quảng cáo trên hai kênh, hãy xác định xem Ti36 sẽ xem mỗi bộ phim bao nhiêu đơn vị thời gian.

Input: watching.inp

• Dòng đầu tiên chứa bốn số nguyên ~n, m, t~ và ~k~ ~(1 \le n, m \le 10^5, 1 \le t \le 10^{18}, 1 \le k \le 10^9)~, trong đó ~n~ là số đoạn quảng cáo trên kênh A, ~m~ là số đoạn quảng cáo trên kênh B, ~t~ là thời điểm đi ngủ và ~k~ là khoảng thời gian được chiếu trên mỗi kênh của mỗi quảng cáo.
• Dòng thứ hai chứa ~n~ số nguyên ~a_i~ ~(1 \le a_1 < a_2 < ... < a_n \le 10^{18}, a_i + k < a_{i+1} \forall i \in [1,n — 1])~, là thời điểm bắt đầu chiếu quảng cáo trên kênh A.
• Dòng thứ ba chứa ~m~ số nguyên ~b_j~ ~(1 \le b_1 < b_2 < ... < b_m \le 10^{18}, b_j + k < b_{j+1} \forall j \in [1,m — 1])~, là thời điểm bắt đầu chiếu quảng cáo trên kênh B.

Output: watching.out

• Đưa ra hai số nguyên là tổng thời gian xem phim "Avengers" trên kênh A và tổng thời gian xem phim "Batman" trên kênh B.

Scoring:

• Subtask ~1~ ~(40\%)~: ~n \le 1000, k, t, a_i, b_j \le 10^6~;
• Subtask ~2~ ~(60\%)~: không có ràng buộc gì thêm.

Sample Input 1

6 5 10 1
1 3 5 7 9 11
2 4 6 8 10

Sample Output 1

5 5

It works … on my machine 😈

Cho bốn số nguyên ~n, x, y, m~. Dãy số ~A~ có độ dài ~n~ được tạo ra theo cách sau:

• ~a_1 = x~;
• ~a_i = (a_{i-1}*x+y) \% m~ với ~2 \le i \le n~.

Dãy số ~B~ là dãy số ~A~ sau khi sắp xếp không giảm.

Tính: ~\sum_{i=1}^{n} (b_i * i) \% m~

Input: smod.inp

• Gồm một dòng chứa bốn số nguyên ~n, x, y, m~ ~(1 \le x, y \le m)~.

Output: smod.out

• In ra một số nguyên là kết quả của bài toán.

Scoring:

• Subtask ~1~ ~(40\%)~: ~n \le 10^5; m \le 10^9~;
• Subtask ~2~ ~(40\%)~: ~n \le 3*10^7; m \le 3*10^7~;
• Subtask ~3~ ~(20\%)~: ~n \le 10^{18}; m \le 10^6~;

Sample Input

3 2 1 10

Sample Output

0

Note

• Dãy số ~A~: ~2, 5, 1~;
• Dãy số ~B~: ~1, 2, 5~;
• Kết quả: ~(1*1+2*2+5*3)\%10=0~.

Cho dãy số ~A~ gồm ~N~ phần tử nguyên dương và một số nguyên dương ~K~. Tìm hai dãy con liên tiếp của dãy ~A~, mỗi dãy gồm đúng ~K~ phần tử (hai dãy không giao nhau), sao cho chênh lệch tổng các phần tử của hai dãy là lớn nhất.

Input:

• Dòng đầu tiên gồm hai số nguyên dương ~N, K~ ~(2 \le N \le 10^6, 1 \le K \le N / 2)~;
• Dòng thứ hai gồm ~N~ số nguyên dương có giá trị không quá ~10^9~ mô tả dãy số ~A~.

Output:

• In ra một số nguyên dương là giá trị chênh lệch lớn nhất tìm được.

Scoring:

• Subtask ~1~ ~(60\%)~: ~ N \le 100~;
• Subtask ~2~ ~(20\%)~: ~ N \le 10^3 ~;
• Subtask ~3~ ~(20\%)~: Không có giới hạn gì thêm.

Sample Input 1

5 2
1 3 2 1 8

Sample Output 1

5

Cho dãy số nguyên dương ~A~ có ~N~ phần tử và một số nguyên không âm ~K~ cho trước. Một dãy số chẵn lẻ đẹp của dãy ~A~ là dãy con liên tiếp thoả mãn:

• Có ít nhất một số chẵn và ít nhất một số lẻ trong dãy con;
• Gọi ~x~ là tổng các số chẵn, ~y~ là tổng các số lẻ trong dãy con thì ~0 \le x - y \le K~ Đếm số lượng các dãy số chẵn lẻ đẹp của dãy ~A~.

Input:

• Dòng đầu tiên gồm hai số nguyên dương ~N, K~;
• Dòng thứ hai gồm ~N~ số nguyên dương có giá trị không quá ~10^9~ mô tả dãy số ~A~.

Output:

• In ra một số nguyên dương là kết quả của bài toán.

Scoring:

• Subtask ~1~ ~(40\%)~: ~ N \le 200; K \le 10^6 ~;
• Subtask ~2~ ~(30\%)~: ~ N \le 2000; K \le 10^6 ~;
• Subtask ~3~ ~(20\%)~: ~ N \le 2*10^5; K = 0 ~;
• Subtask ~4~ ~(10\%)~: ~ N \le 2*10^5; K \le 100 ~;

Sample Input 1

5 5
1 3 2 9 10

Sample Output 1

3

Sample Input 2

3 1
1 3 1

Sample Output 2

0

Cho một xâu ~s~ có độ dài ~n~ chỉ bao gồm các kí tự ~a,b,c~. Một đoạn ~[l,r]~ được gọi là tốt khi và chỉ khi có một kí tự trong đoạn có số lần xuất hiện lớn hơn một nửa độ dài đoạn. Nói cách khác, gọi ~cnt(d,l,r)~ là số lần xuất hiện của kí tự ~d~ trong đoạn ~[l,r]~, ta cần tồn tại một kí tự ~d~ trong đoạn ~[l,r]~ sao cho ~cnt(d,l,r) > (r-l+1)/2~. (Với ~d~ thuộc ~[a,b,c]~)

Hãy in ra độ dài đoạn tốt lớn nhất.

Input

• Dòng đầu gồm số nguyên dương ~n~ miêu tả độ dài xâu. ~(1 \le n \le 10^5)~
• Dòng thứ hai miêu tả xâu ~s~. Xâu ~s~ chỉ bao gồm các kí tự ~a,b,c~ và có độ dài ~n~.

• Ouput

• In ra độ dài đoạn tốt lớn nhất.

Sample Test

Input

7
aabbbcc

Output

5

Giải thích: Chọn đoạn ~[1,5]~.

Mỗi lần bị kẹt trên đường vì tắc đường, An thường nghĩ ra trò chơi để giải trí. Một trong những trò chơi đó là An đọc ~N~ số từ các biển số xe và tìm số nguyên ~M~ ~(M>1)~ sao cho N số đã đọc đều có cùng số dư khi chia cho ~M~. An muốn tìm được càng nhiều số ~M~ như thế càng tốt. Bạn hãy giúp An tìm tất cả các số ~M~ thoả mãn yêu cầu.

Input

• Dòng đầu tiên chứa số nguyên ~N~ ~(2< N <100)~. ~N~ dòng tiếp theo, dòng thứ ~i~ chứa số nguyên ~B_i~ thuộc đoạn ~[1; 10^9]~. Tất cả các số nguyên đôi một khác nhau. Dữ liệu vào luôn đảm bảo tồn tại ít nhất một số ~M~ thoả mãn yêu cầu.

Output

• In ra tất cả các số ~M~ tìm được theo thứ tự tăng dần, các số ghi cách nhau ít nhất một dấu cách.

Subtask

• Có ~60\%~ số test tương ứng với ~0 < B_i \le 10^4~ ~(\forall i \in [1,N])~
• ~40\%~ số test còn lại không giới hạn gì thêm.

Sample Input 1

3
6
34
38

Sample Output 1

2  4

Sample Input 2

5
5
17
23
14
83

Sample Output 2

3

Cho một dãy ~a~ gồm ~n~ phần tử nguyên dương và hai giá trị nguyên dương ~k~, ~x~.

Ta có hàm ~cnt(l,r)~ là số các giá trị ~val~ xuất hiện nhiều hơn hoặc bằng ~x~ lần trong các phần tử thuộc đoạn ~[l,r]~ của dãy ~a~.

Hãy tìm một đoạn con có độ dài bằng ~k~ sao cho ~cnt(l,r)~ của nó là lớn nhất.

Input

• Dòng thứ nhất chứa ~3~ số nguyên dương ~n,k,x~.
• Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy ~a~.

Output

• In ra giá trị của ~cnt(l,r)~ lớn nhất với ~r-l+1=k~.

Constraints

• ~1 \le x \le k \le n \le 2*10^5~.
• ~1 \le a_i \le 2*10^5~.

Subtasks

• Subtask ~1~: ~n \le 1000~ ~(50\%)~
• Subtask ~2~: Không có ràng buộc gì thêm ~(50\%)~

Sample Input 1:

6 4 2
1 2 2 1 3 4

Sample Output 1:

2

Explanation 1:

Chọn đoạn ~[1,4]~.

Sample Input 2:

7 5 3
1 1 2 2 1 1 2 3

Sample Output 2:

1

Explanation 2:

Chọn đoạn ~[1,5]~.

Cho dãy số gồm ~n~ số nguyên ~c_1, c_2, …, c_n~ và số nguyên dương ~m~. Nhiệm vụ của bạn là tìm một đoạn ~b_1,b_2,...,b_k~ ~(1 \le b_1 < b_2 < ... < b_k \le n)~ sao cho ~(\sum c_{b_i}) \% m~ là lớn nhất có thể. Đoạn con tìm được có thể rỗng.

Yêu cầu: Hãy in ra giá trị lớn nhất tìm được.

Input

• Dòng đầu tiên chứa ~2~ số nguyên duyên ~n,m~
• Dòng thứ hai chứa dãy ~c~ gồm ~n~ phần tử.

Output

• Một số nguyên duy nhất là giá trị lớn nhất tìm được.

Constraints

• ~1 \le n \le 40~
• ~1 \le m \le 10^9~
• ~1 \le c_i \le 10^9~

Subtask

• Có ~50\%~ số test ứng với ~n \le 20~.
• Có ~50\%~ số test ứng với ~n \le 40~.

Sample Input 1

4 4
5 2 4 1

Sample Output 1

3

Sample Input 2

3 20
199 41 299

Sample Output 2

19

Cho một số nguyên dương ~n~, hãy phân tích số ~n~ thành tổng của một số số nguyên dương sao cho bội chung nhỏ nhất của chúng là lớn nhất có thể.

Input

• Gồm một số nguyên dương ~n~, ~(1 \le n \le 340)~

Output

• In ra bội chung nhỏ nhất tìm được.

Sample Test

Input:

10

Output:

30

Giải thích: Số ~10~ được phân tích thành tổng của ~3~ số ~{2,3,5}~, bội chung nhỏ nhất của ba số đó bằng ~30~, đây là kết quả lớn nhất có thể.

There are two ways to write error-free programs; only the third one works 😈

Cho một số nguyên ~N~ ~(0 \le N \le 10^{18})~ Đếm xem có bao nhiêu bộ hai số nguyên dương chẵn ~a, b~ sao cho ~a * a * b * b = N~.

Lưu ý: ~a~ và ~b~ có vài trò khác nhau. Ví dụ: cặp ~(6, 4)~ và ~(4, 6)~ được tính là hai cặp khác nhau.

Input:

• Dòng đầu tiên gồm số nguyên ~N~.

Output:

• In ra một số nguyên là số lượng cặp ~a~ và ~b~ thỏa mãn đề bài .

Scoring:

• Subtask ~1~ ~(40\%)~: ~N \le 10^6~;
• Subtask ~2~ ~(40\%)~: ~N \le 10^{12}~;
• Subtask ~3~ ~(20\%)~: ~N \le 10^{18}~.

Sample Input

16

Sample Output

1

Cho một dãy số ~A~ gồm ~N~ phần tử ~A_1,A_2,…,A_N~. Một dãy con liên tiếp từ ~L~ đến ~R~ của dãy số ~A~ là các phần tử ~A_L,A_{L+1},…,A_{R-1},A_R~ ~(1≤L≤R≤N)~. Cho một số nguyên dương ~T~, hãy đếm xem có bao dãy con của ~A~ có tổng các phần tử không quá ~T~.

Input:

• Dòng đầu tiên gồm hai số nguyên dương ~N~ và ~T~ là số lượng phần tử của dãy số ~A~ và số ~T~ cho trước ~(N≤10^6; T≤10^9)~;
• Dòng thứ hai gồm ~N~ số nguyên dương ~A_i~ mô tả các phần tử của dãy số ~A~ ~(1≤i≤N; A_i≤10^9)~.

Output:

Một số nguyên duy nhất là số lượng dãy con thoả mãn yêu cầu đề bài.

Ràng buộc:

• Có 50% số test tương ứng với 50% số điểm có ~N≤100~;
• Có 30% số test khác tương ứng với 30% số điểm có ~N≤5000~;
• 20% số test còn lại tương ứng với 30% số điểm không có ràng buộc gì thêm.

Sample Test 1

Input:

6 8
8 3 2 1 6 9

Output

9

Giải thích

Các dãy con thoả mãn: ~\{8\},\{3\},\{2\},\{1\},\{6\},\{3,2\},\{2,1\},\{1,6\},\{3,2,1\}~

Trong một cơ quan, có ~𝑁~ yêu cầu sử dụng phòng họp trực tuyến. Cơ quan đã đăng kí với cấp trên đường truyền ưu tiên theo ~𝑀~ mốc thời gian được đánh số từ ~1~ đến ~M~. Mỗi yêu cầu đăng kí sử dụng phòng họp trong các mốc thời gian liên tiếp từ ~𝐿~ đến ~𝑅~ ~(1 ≤ 𝐿 ≤ 𝑅 ≤ 𝑀)~. Để tiện cho việc sắp xếp và phục vụ các phòng họp, cần biết mỗi yêu cầu xung đột với bao nhiêu yêu cầu khác (hai yêu cầu gọi là xung đột với nhau nếu có chung ít nhất một mốc thời gian).

Yêu cầu: Cho biết ~𝑁~ yêu cầu sử dụng phòng họp. Với mỗi yêu cầu, hãy tính số lượng yêu cầu xung đột với nó.

Dữ liệu nhập vào từ file văn bản XPH.INP:

• Dòng đầu chứa số hai nguyên ~𝑁,𝑀~ ~(1 ≤ 𝑁 ≤ 2 \times 10^5; \ 1 ≤ 𝑀 ≤ 10^9)~ là số lượng yêu cầu và số lượng mốc thời gian~;~
• ~N~ dòng tiếp theo, dòng thứ ~𝑖~ chứa hai số nguyên ~𝐿_i,𝑅_i \ (1 ≤ 𝐿_i ≤ 𝑅_i ≤ 𝑀; \ 1 ≤ 𝑖 ≤ 𝑁)~ là mốc thời gian bắt đầu và kết thúc của yêu cầu thứ ~𝑖~.

Kết quả ghi ra file văn bản XPH.OUT:

Gồm ~𝑁~ dòng, dòng thứ ~𝑖~ mô tả số lượng yêu cầu xung đột với yêu cầu thứ ~𝑖~ ~(1 ≤ 𝑖 ≤ 𝑁)~.

Ràng buộc

• Có ~25\%~ số test ứng với ~25\%~ số điểm của bài thoả mãn: ~𝑁, 𝑀 ≤ 400;~
• ~25\%~ số test khác ứng với ~25\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 2000;~
• ~25\%~ số test khác ứng với ~25\%~ số điểm của bài thoả mãn: ~𝑀 ≤ 4 \times 10^5;~
• ~25\%~ số test còn lại ứng với ~25\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

5 7
1 2
2 5
3 5
7 7
4 6

Output

1
3
2
0
2

Tỉ phú Vương dự định sẽ xây một thủy cung thu hút khách du lịch. Để thực hiện dự định đó, ông ta đã mua ~n~ chú cá và ~m~ bể thủy sinh. Chú cá thứ ~i~ có sức mạnh là ~a_i~

Vương cần phải quyết định xem, với mỗi chú cá thì ông sẽ đặt vào bể thủy sinh nào. Tuy nhiên, việc này không hề đơn giản, khi ông sẽ phải xem xét đến giới hạn không gian và khả năng kìm hãm sự phát triển lẫn nhau giữa những chú cá trong cùng một bể. Sau những tính toán kĩ lưỡng, ông đã ước tính rằng mức độ bất ổn của mỗi chú cá sẽ bằng tổng sức mạnh của các chú cá nằm cùng bể thủy sinh với chú cá đó (bao gồm cả bản thân chú cá đó).

Yêu cầu: Hãy giúp tỉ phú Vương đặt các chú cá vào các bể thủy sinh sao cho tổng độ bất ổn của các chú cá là nhỏ nhất.

Input

• Dòng đầu tiên gồm hai số nguyên ~n~ và ~m~ ~(1 \le m \le n \le 2000)~ cho biết số chú cá và số bể thủy sinh.
• Dòng thứ hai gồm ~n~ số nguyên ~a_1, a_2, . . . , a_n (1 \le ai \le 10^9 )~ cho biết sức mạnh của các chú cá.

Output

• In một số nguyên duy nhất là tổng độ bất ổn nhỏ nhất của các chú cá.

Subtask

• Có ~20\%~ số test ứng với ~n \le 8~.
• Có ~20\%~ số test khác ứng với ~n \le 15~.
• Có ~20\%~ số test khác ứng với ~m = 2~.
• Có ~30\%~ số test khác ứng với ~n \le 100~.
• ~10\%~ số test còn lại không có giới hạn gì thêm.

Sample Input 1

6 3
9 2 11 3 5 8

Sample Output 1

75

Sample Input 2

4 4
10 20 30 40

Sample Output 2

100

Explanation

Trong ví dụ thứ nhất, một cách đặt cá vào bể thủy sinh tối ưu như sau:

• Đặt chú cá thứ ~1, 6~ vào bể thứ nhất.
• Đặt chú cá thứ ~2, 4, 5~ vào bể thứ hai.
• Đặt riêng chú cá thứ ~3~ vào bể thứ ba. Độ bất ổn của các chú cá lần lượt là ~17 + 10 + 11 + 10 + 10 + 17 = 75~.

Ở ví dụ thứ hai, ta sẽ đặt riêng mỗi chú cá vào một bể thủy sinh.

Trong phòng thí nghiệm chỉ có đúng ba loại cốc có dung tích là ~5 \ (ml)~, ~3 \ (ml)~ và ~2 \ (ml)~. Hỏi cần ít nhất bao nhiêu lần đong nước để lấy được đúng ~N \ (ml)~.

Dữ liệu vào từ file văn bản DONGNUOC.INP:

Một số nguyên dương duy nhất ~N~ ~(2 \le N \le 10^{18})~ là số nước cần đong.

Kết quả ghi ra file văn bản DONGNUOC.OUT:

Một số nguyên dương duy nhất là số lượng lần đong ít nhất thoả mãn yêu cầu đề bài.

Ví dụ

Input

12

Output

3

Giải thích

Đong hai lần bằng cốc ~5 \ (ml)~ và một lần bằng cốc ~2 \ (ml)~.

Input

6

Output

2

Giải thích

Đong hai lần bằng cốc ~3 \ (ml)~.

Cho một dãy số gồm ~N~ số nguyên dương ~a_1, a_2, ..., a_N~ có giá trị không vượt quá ~10^6~. Tìm dãy con liên tiếp ngắn nhất có chứa ít nhất hai số nguyên tố.

Dữ liệu vào từ file văn bản DAYCON.INP:

• Dòng đầu tiên gồm một số nguyên dương ~N \ (N \le 10^6)~ là số lượng phần tử của dãy số;
• Dòng thứ hai gồm ~N~ số nguyên dương ~a_1, a_2, ..., a_N~ lần lượt mô tả các phần tử của dãy số.

Kết quả ghi ra file văn bản DAYCON.OUT:

Một số nguyên duy nhất là số lượng phần tử của dãy con thoả mãn đề bài. Trường hợp không tồn tại dãy con thoả mãn, in ra ~-1~.

Ví dụ

Input

10
3 4 8 4 5 6 1 7 4 6

Output

4

Giải thích

Chọn dãy con từ vị trí thứ ~5~ đến vị trí thứ ~8~: ~5, 6, 1, 7~.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm của bài thoả mãn: ~N \le 10^3; \ a_i \le 10^3~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thoả mãn: ~N \le 10^6; \ a_i \le 10^3~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Bản đồ thành phố X có dạng lưới ô vuông ~M~ hàng ~N~ cột, các hàng được đánh số từ ~1~ tới ~M~, các cột được đánh số từ ~1~ tới ~N~. Mỗi ô vuông trên bản đồ có thể là khu đất trống hoặc một khu dân cư hoặc một siêu thị.

Mỗi siêu thị chỉ có thể phục vụ các khu dân cư có khoảng cách so với nó không quá ~D~, nghĩa là nếu siêu thị nằm ở ô ~(x, y)~ thì nó có thể phục vụ được tất cả các khu dân cư nằm trong hình vuông có ô trái trên là ~(x - D, y - D)~, ô phải dưới là ~(x + D, y + D)~ (như Hình 1).

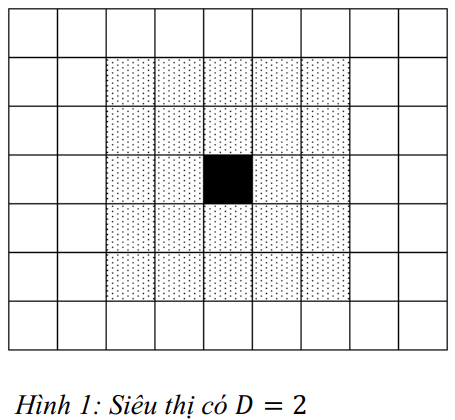
Một khu dân cư gọi là "chất lượng cao" nếu được ít nhất ~K~ siêu thị có thể phục vụ nó. Cho biết bản đồ của thành phố X, hãy đếm số lượng khu dân cư "chất lượng cao".

Dữ liệu vào từ file văn bản KHUDANCU.INP:

• Dòng đầu chứa bốn số nguyên ~M, N, D~ và ~K~ ~(1\le D \le \max(M, N); \ 1\le K\le M \times N)~;
• ~M~ dòng tiếp theo, mỗi dòng gồm ~N~ ký tự, mỗi ký tự biểu diễn một ô vuông bản đồ. Mỗi ký tự sẽ thuộc một trong ba loại sau:
  • . biểu diễn một khu đất trống;
  • P biểu diễn một khu dân cư;
  • M biểu diễn một siêu thị;

Dữ liệu đảm bảo tồn tại ít nhất một khu dân cư và ít nhất một siêu thị.

Kết quả ghi ra file văn bản KHUDANCU.OUT:

Ghi ra một số duy nhất là số khu dân cư "chất lượng cao".

Ví dụ

Input

5 5 1 2
P....
....P
..PM.
.M...
.....

Output

1

Giải thích

Bản đồ minh hoạ thành phố ~X~ như Hình 2.

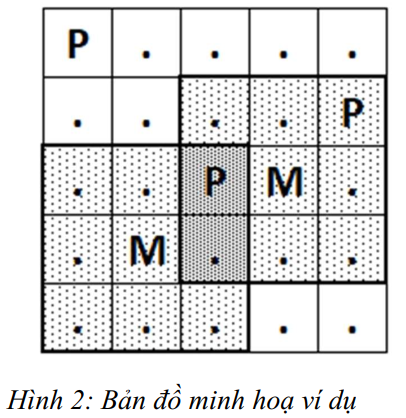
Khu dân cư ở ô ~(1, 1)~ không được siêu thị nào phục vụ;

Khu dân cư ở ô ~(2, 5)~ được một siêu thị có thể phục vụ;

Khu dân cư ở ô ~(3, 3)~ được hai siêu thị có thể phục vụ;

Vậy có một khu dân cư "chất lượng cao".

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thoả mãn: ~M = 1; \ N, D \le 10^3~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~M = 1; \ N \le 10^5~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~2 \le M, N \le 1000;~ số khu dân cư, số siêu thị không vượt quá ~1000~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài thoả mãn: ~2 \le M, N \le 1000~.

Cho một dãy ~a~ gồm ~n~ phần tử nguyên dương và một số nguyên dương ~k~.

Ta có định nghĩa như sau:

• ~MaxSecond(l,r) :~ phần tử lớn thứ hai trong đoạn ~[l,r]~ của dãy ~a~.
• ~MinSecond(l,r) :~ phần tử nhỏ thứ hai trong đoạn ~[l,r]~ của dãy ~a~.
• ~f(l,r) = MaxSecond(l,r) - MinSecond(l,r)~

Hãy tìm một đoạn con ~[l,r]~ dài nhất sao cho ~f(l,r) \le k~.

Input

• Dòng thứ nhất chứa ~2~ số nguyên dương: ~n,k~.
• Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy ~a~.

Output

• In ra số ~X~ là độ dài của đoạn con dài nhất thỏa mãn. Dữ liệu đảm bảo luôn tồn tại kết quả.

Constraints

• ~1 \le n \le 10^5~.
• ~1 \le a_i \le 10^9~.
• ~1 \le k \le 10^9~.

Subtasks

• Subtask ~1~: ~n \le 1000~ ~(50\%)~
• Subtask ~2~: Không có ràng buộc gì thêm ~(50\%)~

Sample Input 1:

5 2
1 4 2 6 5

Sample Output 1:

4

Explanation 1:

Chọn đoạn ~[1,4]~.

Sample Input 2:

7 3
9 1 4 3 12 16 8

Sample Output 2:

4

Explanation 2:

Chọn đoạn ~[2,5]~.

Biểu thức ngoặc đúng được định nghĩa như sau:

• Một xâu rỗng biểu diễn một biểu thức ngoặc đúng;
• Nếu ~A~ là một xâu biểu diễn một biểu thức ngoặc đúng thì ~(A)~ cũng là biểu diễn một biểu thức ngoặc đúng;
• Nếu hai xâu ~A,B~ là xâu biểu diễn biểu thức ngoặc đúng thì ~AB~ cũng là biểu diễn một biểu thức ngoặc đúng.

Thầy Alice muốn tạo một biểu thức ngoặc đúng, có ~n~ vị trí có thể đặt ngoặc. Các vị trí được đánh số từ ~1~ tới ~n~ từ trái sang phải, bắt đầu với giá trị ~s = 0~, tại mỗi vị trí ~(1 \le i\le n)~ thầy Alice có ba lựa chọn:

• Đặt vị trí này là dấu ~(~ và thay ~s = s + a_i~
• Đặt vị trí này là dấu ~)~ và thay ~s = s - a_i~
• Bỏ qua vị trí này.

Sau khi lựa chọn xong, lấy các kí tự từ trái sang phải ở các vị trí đặt dấu ~(~ hoặc ~)~ để tạo được biểu thức ngoặc đúng mà ~s~ đạt giá trị lớn nhất.

Input

• Dòng đầu tiên gồm số nguyên dương ~n~.
• Dòng thứ hai gồm ~n~ số nguyên ~a_1, a_2, . . . , a_n ( |a_i| \le 10^9 )~

Output

• In ra một số nguyên duy nhất là giá trị ~s~ lớn nhất có thể chọn được.

Subtask

• Có ~25\%~ số test ứng với ~n \le 10~.
• Có ~25\%~ số test khác ứng với ~n \le 10^3~.
• Có ~25\%~ số test khác ứng với ~n \le 10^5~ và không có quá ~10^3~ giá trị ~a_i~ khác ~0~.
• Có ~25\%~ số test khác ứng với ~n \le 10^5~.

Sample Input 1

4
0 -5 1 2

Sample Output 1

5

Sample Input 2

9
5 -2 2 3 -4 -4 -1 -2 9

Sample Output 2

21

It's not a bug — it's an undocumented feature 😈

Cho một dãy số nguyên ~A~ gồm ~n~ phần tử, được đánh số ~A_1,A_2,...,A_n~.

Ta có một số định nghĩa như sau:

• Trọng số của đoạn con (ở đây là một đoạn con liên tiếp) là tổng các giá trị ~A_i~ trong đoạn.
• Độ cân bằng của dãy ~A~ là trọng số của đoạn con có trọng số lớn nhất trong dãy số.

Bài toán sẽ thật dễ dàng nếu chỉ yêu cầu tính độ cân bằng của dãy ~A~ được cho, vậy nên ~Watermelon~ - người thầy của muôn quả - đã quyết định tăng độ khó bằng cách sau:

• Đầu tiên, thầy đưa ra một dãy số nguyên gồm ~n~ phần tử ~B_1,B_2,...,B_n~.
• Có tối đa ~k~ lượt chỉnh sửa, mỗi lượt bạn được chọn một đoạn con các phần tử từ vị trí thứ ~l~ đến vị trí thứ ~r~ ~(1 \le l \le r \le n)~ và thực hiện phép gán ~A_i = A_i*B_i~ với ~\forall i \in [l,r]~.

Yêu cầu: Đưa ra được độ cân bằng lớn nhất với tối đa ~k~ lượt chỉnh sửa.

Hoa Quả Sơn đã phải bó cành trước bài toán mới này, bạn hãy giúp họ tìm kiếm câu trả lời.

Input: watermelon.inp

• Dòng đầu tiên gồm hai số nguyên ~n~ và ~k~ ~(1 \le n \le 10^5, 0 \le k \le 10)~.
• Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy số nguyên ~A_1, A_2, ..., A_n~ ~(|A_i| \le 1000)~.
• Dòng thứ ba gồm ~n~ số nguyên dương miêu tả dãy số nguyên ~B_1, B_2, ..., B_n~ ~(|B_i| \le 10)~.

Output: watermelon.out

• In ra một số nguyên duy nhất là độ cân bằng lớn nhất tìm được của dãy ~A~ sau khi sử dụng tối đa ~k~ lượt chỉnh sửa.

Scoring:

• Subtask ~1~ ~(15\%)~: ~k = 0~.
• Subtask ~2~ ~(15\%)~: ~k = 1~ và ~n \le 5000~.
• Subtask ~3~ ~(20\%)~: ~k = 1~.
• Subtask ~4~ ~(25\%)~: ~k = 2~.
• Subtask ~5~ ~(25\%)~: Không ràng buộc gì thêm.

Sample Input 1

5 1
-3 4 -5 2 -2
1 -2 -1 2 1

Sample Output 1

13

Sample Input 2

3 0
-4 -10 -8
2 2 -1

Sample Output 2

-4

Explanation:

• Trong ví dụ thứ nhất, cách tối ưu nhất là chọn đoạn ~[3, 4]~ để tác động. Như vậy dãy ~A~ mới là ~[-3, 4, 5, 4, -2]~. Vậy độ cân bằng của dãy này là ~13~.
• Trong ví dụ thứ ~2~, khi ~k = 0~, bạn không thực hiện lượt chỉnh sửa nào và đưa ra độ cân bằng của dãy ~A~ ban đầu là ~-4~.