Cho số tự nhiên ~N~. Hãy tìm số tự nhiên ~K~ nhỏ nhất sao cho tổng các số lẻ từ ~1~ đến ~K~ lớn hơn tổng các số chẵn từ ~K + 1~ đến ~N~.

Input

• Gồm một dòng chứa một số tự nhiên ~N~ ~(N \le 10^9)~

Output

• Gồm một dòng chứa một số tự nhiên là số ~K~ nhỏ nhất thoả mãn.

Subtask

• Subtask ~1~ (~80\%~ số điểm): ~n \le 1000~.
• Subtask ~2~ (~20\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

10

Sample Output 1

8

Explanation 1

~1 + 3 + 5 + 7 > 10~

Marisa nuôi ~n~ con chim, con chim thứ ~i~ có kích cỡ ~a_i~. Một con chim có kích thước lớn hơn có thể ăn thịt con chim nhỏ hơn. Nếu con chim có kích cỡ ~a_i~ ăn thịt con chim kích cỡ ~a_j~, con chim lớn hơn sẽ có kích cỡ mới là ~a_i+a_j~.

Hãy xác định xem với mỗi con chim, có tồn tại trường hợp mà nó có thể trở thành con chim sống sót cuối cùng không?

Input

• Dòng đầu tiên là số nguyên ~n~, số lượng con chim.
• Dòng thứ hai gồm ~n~ số nguyên dương ~a_i~ ~(a_i \le 10^9)~.

Output

• In một xâu độ dài ~n~, vị trí thứ ~i~ là T nếu con chim thứ ~i~ có thể sống sót đến cuối, ngược lại in ra N.

Subtask

• Subtask ~1~ (~40\%~ số điểm): ~1 \le n \le 1024~.
• Subtask ~2~ (~60\%~ số điểm): ~1 \le n \le 5 \times 10^5~.

Sample Input 1

3
5 4 4

Sample Output 1

TNN

Vì Gojo Satoru quá yếu, nên một ngày đẹp trời Sukuna đã rủ Chau solo bành trướng lãnh địa.

Cả ~2~ solo trên mảnh đất là một bảng hình chữ nhật ~A~, có diện tích ~N \times M~ với ~N~ hàng và ~M~ cột. Kí hiệu ~(i, j)~ là ô nằm trên hàng thứ ~i~, cột thứ ~j~ với các hàng được đánh số từ trên xuống dưới theo thự từ ~1~ đến ~N~, các cột được đánh số từ trái sang phải theo thự từ ~1~ đến ~M~.

Sukuna và Chau đã bành trướng lên lãnh địa này và vẽ ra ~2~ vùng lãnh địa của mình. Trên bảng ~A~, ta kí hiệu ~A (i , j) = 1~ nếu ô đó chứa biên của phần lãnh địa Chau, ~A (i, j) = 2~ nếu ô đó chứa biên của phần lãnh địa của Sukuna, ~A (i, j) = 3~ nếu nó chứa biên của phần lãnh địa của cả hai người, còn ~A (i, j) = 0~ nếu nó là đất trống. Đảm bảo biên của mỗi lãnh địa tạo thành một vòng khép kín. (Biên tức là vòng ngoài của lãnh địa).

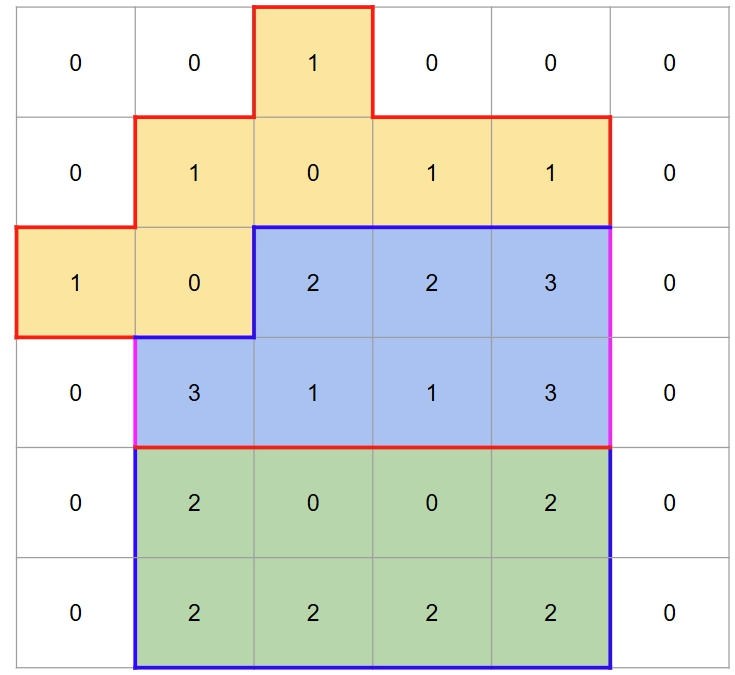
Hình trên là minh họa cho test ví dụ 1.

• Viền màu đỏ là biên của lãnh địa của Chau. Viền màu xanh là biên lãnh địa của Sukuna. Viền màu tím là biên lãnh địa của cả 2.
• Các ô màu cam là các ô thuộc chỉ thuộc lãnh địa của Chau. Các ô màu xanh lá là các ô chỉ thuộc lãnh địa của Sukuna. Các ô màu xanh dương là các ô thuộc lãnh địa của cả hai.

Vì mải dùng Thuật Thức nên Chau không thể dùng Thuật Toán, Chau muốn các bạn tính hộ xem có bao nhiêu ô thuộc cả ~2~ lãnh địa

Yêu cầu: In ra số ô thuộc cả ~2~ lãnh địa.

Input

• Dòng đầu tiên là 2 số tự nhiên ~N, M~ ~(N, M\leq 1000)~ là số hàng và cột của bảng ~A~.
• ~N~ dòng tiếp theo, môi dòng là một hàng của bảng ~A~ và có ~M~ số nguyên không âm nhỏ hơn hoặc bằng 3. Ý nghĩa giá trị của mỗi số nguyên không âm đã nếu ở đề bài ở trên.

Output

• In ra một số nguyên không âm là kết quả của bài toán.

Subtask

• Subtask ~1~ (~25\%~ số điểm): ~N = 1~ .
• Subtask ~2~ (~25\%~ số điểm): ~N, M\leq 100~ và các ô biên của 2 lãnh địa trùng nhau.
• Subtask ~3~ (~25\%~ số điểm): ~N, M\leq 100~.
• Subtask ~4~ (~25\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

6 6
0 0 1 0 0 0
0 1 0 1 1 0
1 0 2 2 3 0
0 3 1 1 3 0
0 2 0 0 2 0
0 2 2 2 2 0

Sample Output 1

7

Quân là một tay cưa gái khét tiếng ở xứ sở Hà Nội Cánh Tay. Cưa gái nhiều nên đã quá ngán, cậu bèn chuyển qua cưa cây.

Hàng cây gồm ~n~ cây, được đánh số từ ~1~ đến ~n~ từ trái qua phải. Ở vị trí thứ ~i~, Quân chỉ được phép trồng cây có độ cao không quá ~h_i~.

Quân muốn tìm một loại cây có độ cao là số nguyên ~H~ ~(H \le h_1, H \le h_n)~ và trồng vào một số vị trí thích hợp, biết rằng cậu chắc chắn sẽ trồng cây vào vị trí thứ ~1~ và thứ ~n~.

Nếu cây ở vị trí thứ ~i~ bị đổ, nó sẽ làm các cây ở vị trí trong khoảng ~[i+1, i+H]~ đổ theo.

Hãy giúp Quân tính xem, độ cao ~H~ nhỏ nhất có thể là bao nhiêu, sao cho nếu Quân chặt đổ cây ở vị trí thứ ~1~ thì cây ở vị trí thứ ~n~ cũng bị đổ theo.

Input

• Dòng đầu tiên chứa một số nguyên dương ~n~ ~(n \leq 10^7)~.
• Dòng thứ hai chứa ~n~ số nguyên không âm ~h_1, h_2, \ldots, h_n~ ~(h_i \leq n)~.

Dữ liệu bảo đảm tồn tại một đáp án hợp lệ.

Output

• In ra một số nguyên dương là kết quả của bài toán.

Subtask

• Subtask ~1~ (~20\%~ số điểm): ~n \le 100~.
• Subtask ~2~ (~20\%~ số điểm): ~n \le 1000~.
• Subtask ~3~ (~20\%~ số điểm): ~n \le 10^5~.
• Subtask ~4~ (~20\%~ số điểm): ~n \le 10^6~.
• Subtask ~5~ (~20\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

10 
10 1 2 0 3 4 5 0 2 10

Sample Output 1

2

Explanation 1

Quân trồng cây độ cao ~2~ ở các vị trí ~1, 3, 5, 7, 9, 10~.

Biểu thức ngoặc là xâu chỉ gồm các kí tự '(', ')', '[', ']', '{', '}'. Biểu thức ngoặc đúng và bậc của biểu thức ngoặc đúng được định nghĩa một cách đệ quy như sau:

• Biểu thức rỗng là biểu thức ngoặc đúng và có bậc bằng ~0~.
• Nếu ~A~ là biểu thức ngoặc đúng có bậc bằng ~k~ thì (A), [A], {A} cũng là một biểu thức ngoặc đúng có bậc bằng ~k \; + \; 1~.
• Nếu ~A~ và ~B~ là hai biểu thức ngoặc đúng và có bậc tương ứng là ~k_1~ và ~k_2~ thì ~AB~ cũng là một biểu thức ngoặc đúng có bậc bằng ~\text{max}(k_1, \; k_2)~.

Ví dụ, ()[()] là một biểu thức ngoặc đúng có bậc bằng ~2~ còn {()[{}]} là một biểu thức ngoặc đúng và có bậc bằng ~3~. Ta sẽ xét hai trường hợp sau:

• ~T \; = \; 1~: biểu thức ngoặc chỉ gồm kí tự '(' và ')'.
• ~T \; = \; 2~: biểu thức ngoặc gồm kí tự '(', ')', '[', ']', '{', '}'.

Với hai số nguyên ~N~, ~K~, người ta tiến hành tạo ra tất cả các biểu thức ngoặc đúng có độ dài ~N~ và bậc không vượt quá ~K~. Sắp xếp các biểu thức ngoặc theo thứ tự từ điển, chú ý rằng '(' < ')' < '[' < ']' < '{' < '}'.

Cho biểu thức ngoặc đúng ~S~, hãy tìm thứ tự của biểu thức ngoặc đúng ~S~.

Input:

• Dòng thứ nhất chứa số nguyên ~T~ ~(1 \leq T \leq 2)~.
• Dòng thứ hai chứa hai số nguyên ~N~ và ~K~ ~(N \leq 3000 \; K \leq N / 2)~.
• Dòng thứ ba chứa ~N~ kí tự của biểu thức ngoặc ~S~.

Output:

• Thứ tự của dãy ngoặc ~S~ lấy dư cho ~10^9 + 7~.

Sample test

Input:

2
8 4
{}(({}))

Output:

1008

Subtask:

• Subtask ~1~ (~20\%~ số điểm): ~T \; = \; 2, \; N \; \leq \; 10~.
• Subtask ~2~ (~15\%~ số điểm): ~T \; = \; 1, \; S \; =~ ()()()...
• Subtask ~3~ (~15\%~ số điểm): ~T \; = \; 2, \; S \; =~ {}{}{}...
• Subtask ~4~ (~25\%~ số điểm): ~T \; = \; 1~.
• Subtask ~5~ (~25\%~ số điểm): ~T \; = \; 2~.

Be careful ... with recursion!

Đất nước HNAms gồm ~n~ thành phố được đánh số từ ~1~ tới ~n~. Đất nước HNAms rất thích bóng đá, ở thành phố thứ ~i~ có số sân vận động là ~a_i~. Do một vài chính sách đặc biệt của Bộ Thể Thao mà số sân vận động của các thành phố là không quá ~m~. Các thành phố của HNAms cũng có ~n-1~ con đường hai chiều để kết nối các thành phố lại. Con đường thứ ~i~ sẽ nối hai thành phố ~u_i~ và ~v_i~, đảm bảo rằng mọi cặp thành phố đều có lộ trình di chuyển tới nhau. Nói cách khác, như bao đất nước trong thế giới OI, HNAms có thể ví như một đồ thị dạng cây.

Bộ Xây Dựng đã tạo ra một phương pháp để đánh giá độ hiệu quả trong giao thông của một tổ hợp các thành phố:

• Giả sử ta có một tập thành phố ~u_1,u_2,...,u_k~, độ hiệu quả trong giao thông của tập hợp thành phố này chính bằng đường đi ngắn nhất nếu có thể xuất phát tại một thành phố tùy ý và đi qua hết các thành phố trong tập. Đường đi ở HNAms được tính theo số con đường mà lộ trình này đi qua.

Để hiểu rõ hơn về cách tính độ hiệu quả, hãy nhìn vào hình vẽ trên:

• Giả sử tập thành phố là ~[3,4,5]~, độ hiệu quả của tổ hợp này là ~5~, bởi ta sẽ đi theo lộ trình: ~3 \rightarrow 2 \rightarrow 1 \rightarrow 4 \rightarrow 1 \rightarrow 5~. Dễ thấy không có lộ trình nào có thể ngắn hơn.
• Giả sử tập thành phố là ~[2,5]~, độ hiệu quả của tổ hợp này là ~2~ với lộ trình: ~2 \rightarrow 1 \rightarrow 5~.
• Đối với tập thành phố rỗng hoặc có số thành phố bằng ~1~, độ hiệu quả được đánh giá là bằng ~0~.

Vì là một người đam mê bóng đá, chủ tịch HuySalad quyết định ăn mừng ~120~ năm sinh nhật của FIFA bằng việc tổ chức một mùa giải bóng đá bất tận, trải dài từ ngày ~1~ tới ngày ~m~ (hãy cố chấp nhận rằng thực sự có nhiều ngày như vậy). Vào ngày thứ ~x~ ~(1 \le x \le m)~, các trận đấu bóng đá sẽ được tổ chức tại các thành phố có số sân vận động chia hết cho ~x~.

Như vậy, lưu lượng khách di chuyển sẽ là rất lớn, Chính Phủ giao cho bạn - Bộ Công Nghệ - đối với mỗi ngày, hãy đánh giá độ hiệu quả của tổ hợp thành phố được tổ chức bóng đá. Nói cách khác, đối với mỗi ngày thứ ~x~ ~(1 \le x \le m)~, bạn sẽ phải đánh giá độ hiệu quả của tập thành phố ~[u_1,u_2,...,u_k]~ thỏa mãn ~x \mid a[u_i] ~ ~(\forall 1 \le i \le k)~.

Input:

• Dòng thứ nhất chứa hai số nguyên dương ~n,m~ ~(1 \le n \le 2 \times 10^5, 1 \le m \le 10^5)~
• Dòng thứ hai chứa ~n~ số nguyên dương, số thứ ~i~ là ~a_i~, miêu tả số sân vận động ở thành phố ~i~ ~(1 \le a_i \le m)~.
• ~n-1~ dòng tiếp theo, dòng thứ ~i~ gồm hai số nguyên dương ~u_i~ và ~v_i~ miêu tả con đường hai chiều nối từ thành phố ~u_i~ tới thành phố ~v_i~.

Output:

• In ra ~m~ dòng, dòng thứ ~i~ là độ hiệu quả của tổ hợp thành phố được sử dụng trong ngày thứ ~i~.

Subtask:

• Subtask ~1~ (~15\%~ số điểm): Tất cả các con đường thứ ~i~ trong khoảng ~[1,n-1]~ có dạng ~u_i = i, v_i = i+1~.
• Subtask ~2~ (~10\%~ số điểm): ~n \le 10, m = 1~.
• Subtask ~3~ (~15\%~ số điểm): ~m = 1~
• Subtask ~4~ (~10\%~ số điểm): ~m = 2~
• Subtask ~5~ (~30\%~ số điểm): ~n \le 5 \times 10^4, m \le 10^4~
• Subtask ~6~ (~20\%~ số điểm): Không có giới hạn gì thêm.

Sample Input 1

5 1
1 1 1 1 1
1 3 
3 2
1 4
3 5

Sample Output 1

5

Explanation 1

Do ~m=1~ nên chỉ có ngày đầu tiên được tổ chức bóng đá, do tất cả các thành phố đều có số sân vận động chia hết cho ~1~, nên ta có tập ~[1,2,3,4,5]~.

Độ hiệu quả của tập này là ~5~, với lộ trình ~5 \rightarrow 3 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 4~

Sample Input 2

6 5
2 2 3 4 3 1
1 3 
3 2
3 4
1 5
1 6

Sample Output 2

7
4
2
0
0

Explanation 2

Ta có các tập thành phố sau:

• Ngày ~1~: ~[1,2,3,4,5,6]~.
• Ngày ~2~: ~[1,2,4]~
• Ngày ~3~: ~[3,5]~
• Ngày ~4~: ~[4]~
• Ngày ~5~: ~[]~
• Do ngày ~4~ chỉ có một và ngày ~5~ không có thành phố nào trong tập, độ hiệu quả của chúng đều bằng ~0~.