Bạn được nhận một xâu ~A~ gồm ~n~ kí tự Latin in thường và một số nguyên dương ~k~. Ta xây dựng xâu ~S = A \times k~, tức là xâu ~S~ được xây dựng bằng cách viết ra ~k~ lần xâu ~A~.

Để tăng độ yêu trường cho học sinh, ~mrtee~ quyết định giao cho các học sinh công việc đếm các xâu kí tự có dạng ams xuất hiện trong ~S~ dưới dạng một xâu con liên tiếp.

Ví dụ: ~A = amser~, ~k = 2~ ~\Rightarrow S = amseramser~. Có ~2~ xâu con liên tiếp của ~S~ bằng ams.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~n,k~ ~(1 \le n \le 2 \times 10^5)~
• Dòng thứ ~2~ là xâu ~A~ gồm ~n~ phần tử.

Output:

• In ra số lượng xâu con liên tiếp bằng ams xuất hiện trong ~S~.

Subtask:

• Subtask ~1~ (~50\%~ số điểm): ~k = 1~.
• Subtask ~2~ (~50\%~ số điểm): Không có giới hạn gì thêm.

Sample Input 1

5 2
amser

Sample Output 1

2

Sample Input 2

3 2
msa

Sample Output 2

1

Cho hai dãy ~a~ và ~b~ gồm ~n~ phần tử nguyên dương. Bạn được nhận thêm một số nguyên dương ~k~, hãy đếm số cặp ~(i,j)~ ~(1 \le i,j \le n)~ sao cho ~\overline{a_ib_j}~ ~\vdots~ ~k~.

Nói cách khác, hãy đếm số cặp ~(i,j)~ sao cho số nguyên dương ~X~ được tạo bởi cách viết liền ~a_i~ và ~b_j~ với nhau chia hết cho số nguyên dương ~K~ cho trước.

Ví dụ:

• ~a_i = 5, b_j = 77 \Rightarrow X = 577~
• ~a_i = 66, b_j = 99 \Rightarrow X = 6699~

Input

• Dòng đầu tiên gồm số hai nguyên dương ~n~ và ~k~ ~(1 \le n,k \le 3 \times 10^5)~
• Dòng thứ hai gồm ~n~ số nguyên dương ~a_1,a_2,...,a_n~ ~(1 \le a_i \le 3 \times 10^5)~.
• Dòng thứ hai gồm ~n~ số nguyên dương ~b_1,b_2,...,b_n~ ~(1 \le b_i \le 3 \times 10^5)~.

Output:

• Gồm một dòng in ra số cặp ~(i,j)~ thỏa mãn.

Subtask:

• Subtask ~1~ (~40\%~ số điểm): ~n \le 2000~.
• Subtask ~2~ (~30\%~ số điểm): ~a_i,b_j \le 2000~ ~\forall i,j \in [1,n]~.
• Subtask ~3~ (~30\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

4 3
1 4 3 6
11 2 4 21 

Sample Output 1

6

Explanation 1

Có các cặp sau:

• ~(1,1) = 111~
• ~(1,2) = 12~
• ~(2,1) = 411~
• ~(2,2) = 42~
• ~(3,4) = 321~
• ~(4,4) = 621~

Marisa cần chia một cây nấm thành ba miếng nhỏ hơn. Mũ nấm có dạng hình tròn, được cấu tạo từ ~n~ phần, phần thứ ~i~ có kích cỡ ~a_i~.

Ví dụ với ~a = \{1, 3, 4, 4, 4, 2 ,5\}~

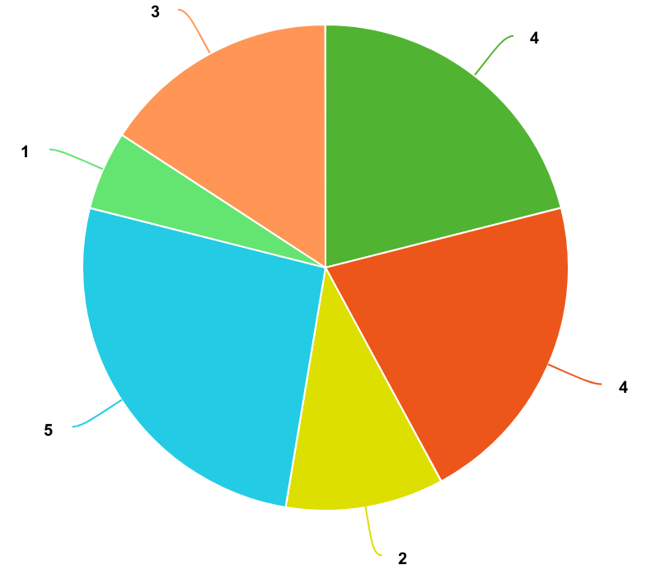
Một miếng nấm sẽ chỉ được gồm các phần liên tiếp. Hãy tìm cách chia sao cho miếng nấm có kích cỡ nhỏ nhất là lớn nhất.

Input

• Dòng đầu tiên gồm số nguyên ~n~.
• Dòng thứ hai gồm ~n~ số nguyên ~a_i~.

Output

• Một số nguyên là kích cỡ lớn nhất có thể của miếng nấm nhỏ nhất.

Giới hạn

• Trong mọi test, ~3 \le n \le 10^5, 1\le a_i \le 10^9~
  • Subtask 1 (25% số điểm): ~1 \le n \le 100~
  • Subtask 2 (25% số điểm): ~1 \le n \le 400~.
  • Subtask 3 (25% số điểm): ~1 \le n \le 8000~.
  • Subtask 4 (25% số điểm): Không có giới hạn gì thêm.

Ví dụ

Input:

7
1 3 4 4 4 2 5

Output:

7

Cho một cây gồm ~n~ đỉnh gồm ~n-1~ cạnh. Cạnh thứ ~i~ có dạng ~(u_i,v_i, w_i)~, kết nối đỉnh ~u_i~ với đỉnh ~v_i~ và có độ dài là một số nguyên dương ~w_i~.

Gọi ~D(u,v)~ là khoảng cách giữa hai đỉnh ~u~ và ~v~ trên cây (được tính bằng tổng trọng số trên cạnh mà đường đi từ ~u~ tới ~v~ đi qua). Ta có hàm ~S(i)~ là tổng khoảng cách từ ~i~ tới tất cả các đỉnh trên cây:

• ~S(i) = \sum_{u=1}^{n} D(i,u)~.

Với mỗi đỉnh ~u~ trên cây, bạn được phép thử gán giá trị của một cạnh bất kì trên cây bằng ~0~ (tức là gán một giá trị ~w_i = 0~), sao cho giá trị ~S(u)~ mới, ta tạm gọi là ~S(u)'~ là nhỏ nhất có thể. Lưu ý rằng, mỗi lần thử là độc lập với nhau, ta không thực sự gán cạnh nào bằng ~0~ trong cây gốc cả.

Để tránh biến bài toán quá khó, với mỗi lần thử, các bạn không cần in ra ~S(u)'~, mà chỉ cần in ra độ chênh lệch giữa hai giá trị cũ và mới, nói cách khác in ra ~S(u) - S(u)'~.

Input

• Dòng đầu tiên gồm số nguyên dương ~n~ ~(1 \le n \le 3 \times 10^5)~
• ~n-1~ dòng sau, dòng thứ ~i~ gồm ba số nguyên dương ~(u_i,v_i,w_i)~ ~(1 \le u_i, v_i \le n, 1 \le w_i \le 10^6)~ miêu tả cạnh thứ ~i~ của cây.

Output:

• Gồm một dòng gồm ~n~ số nguyên, số thứ ~i~ là ~S(i)~ nhỏ nhất thu được nếu ta thử gán tối ưu nhất có thể.

Subtask:

• Subtask ~1~ (~20\%~ số điểm): ~n \le 200~.
• Subtask ~2~ (~20\%~ số điểm): ~u_i = i, v_i = i+1~ ~\forall i \in [1,n-1]~.
• Subtask ~3~ (~20\%~ số điểm): ~w_i = 1~ với mọi ~i~ và ~n \le 2000~.
• Subtask ~4~ (~20\%~ số điểm): ~w_i = 1~ với mọi ~i~.
• Subtask ~5~ (~20\%~ số điểm): Không có giới hạn gì thêm.

Sample Input 1

6
1 2 2
1 4 1
1 3 1
2 6 3
3 5 6

Sample Output 1

6 8 6 6 30 15

Explanation 1

Đối với đỉnh ~1~, giả sử ta gán cạnh ~(3,5) = 0~, ta sẽ giảm được ~S(1)~ đi một lượng là ~6~ của ~D(5,1)~.

Đối với đỉnh ~2~, giả sử ta gán cạnh ~(1,2) = 0~, ta sẽ giảm được ~S(2)~ đi một lượng là ~8~.

Với đỉnh ~5~, cách gán tối ưu nhất là gán ~(3,5) = 0~.

Với đỉnh ~6~, ta gán ~(2,6) = 0~ để thu được kết quả là giảm đi ~15~ đơn vị.

Cho thẻ bài có hai mặt hình con hươu (🦌) và hình con người (🧍‍♂️).

Các thẻ bài được xếp theo thứ tự: ~a~ thẻ bài hình con hươu, ~b~ thẻ bài hình con người, ~c~ thẻ bài hình con hươu, ~d~ thẻ bài hình con người, ~e~ thẻ bài hình con hươu.

Có ~q~ thao tác, lật thẻ bài từ vị trí ~l~ đến vị trí ~r~ (nghĩa là người biến thành hươu và hươu biến thành người), tốn thời gian là ~r - l + 1~. Hỏi thời gian ít nhất để lật toàn bộ các thẻ bài thành hươu là bao nhiêu.

Input

• Dòng đàu tiên gồm năm số nguyên ~a,b,c,d,e~.
• Dòng thứ hai gồm số nguyên ~q~.
• ~q~ dòng tiếp theo, mỗi dòng gồm hai số nguyên ~l,r~.

Output

• Một số nguyên duy nhất là thời gian ít nhất để lật tất cả các thẻ bài thành thẻ bài hươu. Trong trường hợp không có cách lật thỏa mãn, in ra -1.

Giới hạn

• Trong mọi test, ~1 \le a,b,c,d,e,q \le 10^5, 1 \le l \le r \le a+b+c+d+e~:
  • Subtask 1 (30% số điểm): ~1 \le q \le 10~
  • Subtask 2 (30% số điểm): ~1 \le a,b,c,d,e \le 50~.
  • Subtask 3 (40% số điểm): Không có giới hạn gì thêm

Ví dụ

Input:

1 1 1 1 1
2
2 4
3 3

Output:

4

Cho ma trận vuông ~n \times n~, các hàng được đánh số từ ~1~ tới ~n~, các cột được đánh số từ ~1~ tới ~n~. Các ô được sắp xếp theo thứ tự từ trái sang phải, từ trên xuống dưới, ô ~(i,j)~ có giá trị là ~a_{i,j}~.

Ivan Tèo đang đứng ở ô ~(1,1)~ của ma trận, trong mỗi lần đi, cậu chỉ có thể đi sang phải hoặc xuống dưới, nói cách khác, nếu đang ở ô ~(i,j)~, cậu chỉ có thể đi sang ô ~(i+1,j)~ hoặc ~(i,j+1)~. Gọi ~Best(i,j)~ là giá trị lớn nhất có thể nếu Ivan Tèo đi từ ô ~(1,1)~ tới ô ~(i,j)~. Vì cảm thấy rằng nếu chỉ hỏi các ~Best(i,j)~ thì quả là nhàm chán và không đánh giá đúng được tiềm năng của Tèo, ~mrhee~ quyết định tạo ra một giá trị mới như sau:

• Gọi ~S~ là tổng các ~Best(i,j)~ của mọi ô ~(i,j)~ trên ma trận.
• Nói cách khác, ~S = \sum Best(i,j)~, với mọi ~(1 \le i,j \le n)~.

Vì lại cảm thấy việc in ra ~S~ của ma trận hiện tại là quá dễ với Tèo, ~mrhee~ quyết định tạo ra ~q~ sự thay đổi, sự thay đổi thứ ~i~ có dạng như sau:

• Cho ba số nguyên ~u_i,v_i,delta_i~ ~(1 \le u_i,v_i \le n, -1\le delta_i \le 1)~, tức gán giá trị ~a_{u_i,v_i} = a_{u_i,v_i} + delta_i~.
• Sau mỗi truy vấn, hãy in ra giá trị ~S~ của ma trận mới.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~n,q~ ~(1 \le n \le 1000, 1 \le q \le 3 \times 10^4)~
• ~n~ dòng sau, dòng thứ ~i~ gồm ~n~ số nguyên, số thứ ~j~ miêu tả giá trị ~a_{i,j}~ ~(-10^2 \le a_{i,j} \le 10^2)~ của ma trận.
• ~q~ dòng tiếp theo, mỗi dòng gồm ba số nguyên ~u_i,v_i,delta_i~ ~(1 \le u_i,v_i \le n, -1 \le delta_i \le 1)~ miêu tả truy vấn thứ ~i~.

Output:

• Gồm một dòng in ra số cặp ~(i,j)~ thỏa mãn.

Subtask:

• Subtask ~1~ (~25\%~ số điểm): ~q \le 10~.
• Subtask ~2~ (~25\%~ số điểm): Ô ~(u_i,v_i)~ trong mọi truy vấn là giống nhau và ~q \le 3000~, đồng thời ~delta_i = 1~ với mọi truy vấn.
• Subtask ~3~ (~30\%~ số điểm): ~q \le 3000~
• Subtask ~4~ (~20\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

2 2
1 2
2 2
1 2 0
2 1 1

Sample Output 1

12
14

Sample Input 2

4 4
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
1 1 1
2 2 -1
3 1 1
1 3 -1

Sample Output 2

196
195
203
199

Explanation

Ở ví dụ ~1~, sau truy vấn đầu, bảng không thay đổi gì, ta có các ~Best(i,j)~ như sau:

• ~Best(1,1) = 1~
• ~Best(1,2) = 3~
• ~Best(2,1) = 3~
• ~Best(2,2) = 5~

Sau khi tăng ô ~(2,1)~ lên ~4~ đơn vị, ta có:

• ~Best(1,1) = 1~
• ~Best(1,2) = 3~
• ~Best(2,1) = 4~
• ~Best(2,2) = 6~