Ams QG 17-07-25
tricnt
Nộp bàiPoint: 100
Cho một bảng kí tự ~N \times N~ gồm hai loại kí tự . và #, bạn cần phải đếm số lượng tam giác được tạo bởi các kí tự # trong bảng. Ví dụ về các tam giác:
#
# ###
# ### #####, ...
Các hình sau đây không phải tam giác:
# #
## ### ## #
# # # ##, ...
Cụ thể, một tam giác có độ cao ~h~ gồm ~h~ hàng, hàng thứ ~i~ từ trên xuống có ~2i - 1~ kí tự # và được đặt sao cho kí tự thứ ~i~ ở mỗi hàng là thẳng cột với nhau.
Input
- Dòng đầu tiên chứa số nguyên dương ~N~ ~(1 \le N \le 2000)~
- ~N~ dòng sau, mỗi dòng chứa ~N~ kí tự biểu diễn hàng thứ ~i~ của bảng.
Output
- In ra số tam giác trong bảng.
Sample
Input
5
.#.#.
#####
###..
.#...
###..
Output
18
marble
Nộp bàiPoint: 100
Trước mặt Hiếu hiện tại có ~N~ viên bi, viên thứ ~i~ có kích thước là ~A_i~. Hiếu có thể thực hiện một trong hai thao tác sau:
- Chọn hai viên bi liên tiếp có kích thước bằng nhau và gộp chúng lại. Hai viên bi này sau đó sẽ biến mất và được thế chỗ bởi viên bi mới có kích thước bằng tổng kích thước của hai viên bi cũ.
- Chọn ba viên bi liên tiếp, sao cho viên thứ nhất và viên thứ ba có kích thước bằng nhau và gộp ba viên bi này lại. Ba viên bi này sau đó sẽ biến mất và được thế chỗ bởi viên bi mới có kích thước bằng tổng kích thước của ba viên bi cũ.
Hãy tìm viên bi có kích thước lớn nhất mà Hiếu có thể tạo ra, nếu sử dụng các thao tác trên một cách tối ưu.
Input
- Dòng đầu chứa một số nguyên dương ~N~ ~(1 \le N \le 400)~.
- Dòng sau chứa ~N~ số nguyên dương ~A_1, A_2, \ldots, A_N~ ~(1 \le A_i \le 10^6)~.
Output
- In ra một số nguyên duy nhất là kết quả bài toán.
Sample
Input
6
1 1 2 1 3 4
Output
11
Giải thích:
- Đầu tiên, Hiếu gộp ba viên bi thứ 1, 2 và 3, dãy bi trở thành ~[1, 4, 3, 4]~.
- Hiếu gộp tiếp ba viên ~2, 3, 4~ và từ đó có viên bi kích thước ~11~.
Bảng xếp hạng
Nộp bàiPoint: 150
Khi chuẩn bị contest, Hùng luôn luôn muốn tạo ra một bảng xếp hạng phong phú nhất có thể, tức có nhiểu điểm số khác nhau xuất hiện trên đó. Theo Hùng, contest như vậy mới phân loại được trình độ các thí sinh, giúp các thí sinh phần nào biết được thực lực của mình, đồng thời tránh việc bị chửi "speedforces", "mathforces" ...
Trong contest ngay tiếp theo, Hùng đã trình làng ~N~ bài tập và tất cả các bài đều có điểm số là ~100~. Bài thứ ~i~ có ~M_i~ test, và nếu đúng test thứ ~j~ của bài đó thì sẽ được ~A_{i, j}~ điểm. Để tính độ phong phú của bộ bài này, Hùng muốn tính xem có bao nhiêu điểm số khác nhau mà thí sinh có thể nhận được trong tất cả các trường hợp đúng sai từ mỗi test của từng bài. Bạn hãy tính xem có bao nhiêu điểm số khác nhau mà thí sinh có thể nhận được từ ~N~ bài này nhé!
Input
- Dòng đầu chứa số nguyên dương ~N~ ~(1 \le N \le 10^4)~.
- Dòng thứ ~i~ trong ~N~ dòng sau có dạng như sau: ~M_i \ A_{i,1} \ A_{i,2} \ \ldots \ A_{i,M_i}~. ~(1 \le A_{i,j} \le 100, A_{i,1} + A_{i,2} + \ldots + A_{i,M_i} = 100)~.
Output
In ra một số nguyên duy nhất là số lượng điểm số mà thí sinh có thể nhận được từ contest của Hùng.
Subtasks
- Subtask 1: ~(30\%)~ số điểm: ~M_1 + M_2 + \ldots + M_N \le 18~.
- Subtask 2: ~(30\%)~ số điểm: ~N \le 1000~.
- Subtask 3: ~(40\%)~ số điểm: Không có giới hạn gì thêm.
Sample Input
2
2 50 50
2 25 75
Sample Output
9
Giải thích: Các điểm số thí sinh có thể nhận được là ~0, 25, 50, 75, 100, 125, 150, 175, 200~.
XOR Slimes
Nộp bàiPoint: 150
Có ~N~ con slime trên một trục số kéo dài về hai phía. Con slime thứ ~i~ từ trái sang có một số nguyên ~A_i~ và nằm tại vị trí ~X_i~.
Slime có thể thực hiện các thao tác hợp nhất nhiều lần tùy ý như sau:
Chọn ~2~ con slime để hợp nhất.
- Gọi vị trí của chúng là ~X_p, X_q~ và số nguyên chúng mang là ~A_p, A_q~.
Chọn một số thực ~x~ tùy ý.
- Hai con slime sẽ di chuyển đến vị trí ~x~ rồi hợp nhất thành một con slime mới.
- Chi phí di chuyển được tính là: ~|X_p - x| + |X_q - x|~
- Số nguyên mà slime mới mang theo sẽ là ~A_p \oplus A_q~ (~\oplus~ là phép XOR nhị phân).
Gọi ~C~ là tổng chi phí di chuyển của tất cả các lần hợp nhất.
Gọi ~S~ là tổng số nguyên của các con slime còn lại sau khi hợp nhất.
Yêu cầu: Tìm giá trị ~C + S~ nhỏ nhất có thể.
Input
- Dòng đầu tiên chứa một số nguyên dương ~N~ ~(1 \le N \le 5000)~
- Dòng thứ hai chứa ~N~ số nguyên ~X_1, X_2, \ldots, X_N~ ~(1 \le X_1 \lt X_2 \lt \ldots \lt X_N \le 10^9)~
- Dòng cuối cùng chứa ~N~ số nguyên ~A_1, A_2, \ldots, A_N~ ~(1 \le A_N \lt 2^{30})~
Output
- In ra một số nguyên duy nhất là giá trị ~C + S~ nhỏ nhất có thể tìm được.
Sample Input 1
3
2 4 5
2 1 6
Sample Output 1
8
Giải thích:
Khi con slime thứ ~1~ và con slime thứ ~3~ hợp nhất tại vị trí ~x = 3.5~, số nguyên của slime mới sẽ là:
$$
2 \oplus 6 = 4
$$
Chi phí di chuyển tại thời điểm này là:
$$
|2 - 3.5| + |5 - 3.5| = 3
$$
Nếu dừng quá trình hợp nhất ở đây, tổng chi phí di chuyển là ~C = 3~ và tổng các số nguyên còn lại là ~S = 5~.
Khi đó, giá trị ~C + S~ là:
$$
C + S = 8
$$
Có thể chứng minh không có cách hợp nhất nào để ~C + S < 8~.
Sample Input 2
4
1 4 5 7
1 1 1 1
Sample Output 2
3
Sample Input 3
4
10 20 30 40
1 1 1 1
Sample Output 3
4
Sample Input 4
3
3 7 15
5 3 6
Sample Output 4
12
rjump
Nộp bàiPoint: 150
Trên một mặt phẳng tọa độ có ~N~ điểm ~(x_1, y_1), (x_2, y_2) \ldots, (x_N, y_N)~ và không điểm nào trùng với ~(0, 0)~. Ở điểm ~(0, 0)~ có một con thỏ, và con thỏ này muốn nhảy đến các điểm trên mặt phẳng nhiều lần nhất, với điều kiện: lần nhảy sau phải ngắn hơn lần trước đó.
Cụ thể hơn, gọi ~OP_1 P_2 \ldots P_k~ là dãy các điểm trên hành trình của con thỏ (trong đó ~O~ là điểm ~(0, 0)~ và ~P_1, P_2, \ldots, P_k~ phải là một trong các điểm có sẵn). Ta cần tìm một dãy các điểm dài nhất, sao cho ~OP_1 > P_1 P_2 > P_2 P_3 \ldots > P_{k - 1} P_k~.
Hãy tìm số bước nhảy nhiều nhất có thể cho hành trình của con thỏ. Chú ý là con thỏ có thể nhảy lại đến một điểm trước đó, nhưng không được đứng yên (tức ~P_{i - 1} \neq P_i~).
Input
- Dòng đầu chứa số nguyên dương ~N~ ~(1 \le N \le 2000)~.
- ~N~ dòng sau, dòng thứ ~i~ chứa hai số nguyên ~x_i, y_i~ ~(-10000 \le x_i, y_i \le 10000, (x_i, y_i) \neq (0, 0))~ là tọa độ của điểm thứ ~i~.
Output
- In ra một số nguyên duy nhất là đáp án của bài toán.
Scoring
- Subtask 1 ~(30\%)~: ~N \le 20~.
- Subtask 2 ~(30\%)~: ~N \le 200~.
- Subtask 3 ~(40\%)~: Không có giới hạn gì thêm.
Sample
Input
5
2 2
0 1
3 3
-2 4
2 3
Output
6
Giải thích: Có một cách di chuyển tối ưu như sau:
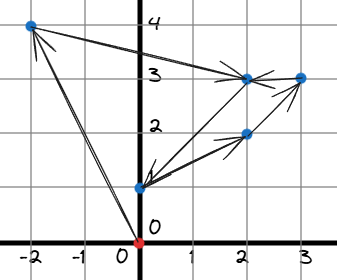
strf2
Nộp bàiPoint: 200
Cho một xâu ~S~ gồm các chữ cái tiếng anh thường. Gọi ~f(s)~ là số lần xâu ~s~ xuất hiện trong ~S~ dưới dạng một xâu con không liên tiếp (~s~ có thể rỗng). Ví dụ với ~S = aabba~, ta có ~f('') = 1, f('a') = 3, f('b') = 2, f('ab') = 4, f('abba') = 2, f('aba') = 4, \ldots~
Hãy tính ~\sum f(s)^2~ modulo ~M~, với ~M~ cho trước.
Input
- Dòng đầu chứa xâu ~S~ ~(1 \le |S| \le 10000)~ gồm các chữ cái tiếng anh thường.
- Dòng thứ hai chứa số nguyên dương ~M~ ~(1 \le M \le 10^9)~.
Output
- In ra một số nguyên duy nhất là đáp án bài toán modulo ~M~.
Scoring
- ~30\%~ số test có ~|S| \le 20~.
Sample
aabba
3612
Output
80
