Cho bảng ~a~ có kích thước ~n \times m~. Có ~q~ truy vấn, mỗi truy vấn có dạng: ~(x,y,u,v)~, yêu cầu in ra tổng của hình chữ nhật có ô trái trên là ~(x,y)~ và ô phải dưới là ~(u,v)~ của bảng.

Input

• Dòng đầu tiên chứa ba số nguyên dương ~n,m,q~.
• ~n~ dòng sau, mỗi dòng gồm ~m~ số nguyên miêu tả bảng ~a~.
• ~q~ dòng sau, mỗi dòng gồm ~4~ số nguyên dương ~x,y,u,v~ miêu tả truy vấn.

Output

• Với mỗi truy vấn, in ra tổng của hình chữ nhật con cần tính.

Điều kiện

• ~1 \le n,m \le 500~.
• ~1 \le q \le 10^5~.
• ~1 \le x \le u \le n~
• ~1 \le y \le v \le m~.
• ~1 \le a_{i,j} \le 500~

Subtask

• ~50\%~ số điểm: ~q \le 100~
• ~50\%~ số điểm: ~q \le 10^5~.

Ví dụ

Input 1:

3 3 4
1 2 3
3 2 1
1 2 3
1 1 3 3 
2 2 2 3
1 2 3 2
2 1 3 2

Output 1:

18
3
6
8

Cho một dãy ~a~ gồm ~n~ phần tử. Ban đầu tất cả phần tử đều có giá trị bằng ~0~. Có ~m~ thao tác, thao tác thứ ~i~ gồm ba số nguyên ~L,R,X~ có nghĩa là tăng các phần tử từ vị trí thứ ~L~ tới vị trí thứ ~R~ lên ~X~ đơn vị.

Hãy tìm cách bỏ đi một thao tác để sau khi thực hiện hết ~M-1~ thao tác còn lại thì giá trị lớn nhất của dãy số là nhỏ nhất.

Input

• Dòng thứ nhất chứa ~2~ số nguyên dương ~n,m~.
• ~m~ dòng sau, mỗi dòng gồm ba số nguyên dương ~L,R,X~.
  
  

Output

• In ra giá trị lớn nhất của dãy số sau khi bỏ đúng một thao tác thỏa mãn yêu cầu đề bài.
  
  

Constraints

• ~1 \le n,m \le 10^5~.
• ~|x| \le 10^9~.
  
  

Subtasks

• ~25\%~ số test: ~N \le 10^2, M \le 10^2~.
• ~25\%~ số test: ~N \le 10^5, M \le 10^2~.
• ~25\%~ số test: ~N \le 10^2, M \le 10^5~.
• ~25\%~ số test: ~N \le 10^5, M \le 10^5~.
  
  

Sample Test 1

Input:

5 2
1 3 3
2 5 2

Output:

2

Sample Test 2

Input:

5 3
1 3 3
2 5 2 
5 5 8

Output:

5

Cho hai dãy ~a~ và ~b~ cùng có ~n~ phần tử nguyên. Ta định nghĩa hàm ~sum(x,y)~ ~(1 \le x,y \le n)~ như sau:

• Nếu ~x \le y~ thì ~sum(x,y) = a_x + a_{x+1} + a_{x+2} + ... + a_y~.
• Nếu ~x > y~ thì ~sum(x,y) = b_x + b_{x-1} + b_{x-2} + ... + b_y~.

Nhiệm vụ của bạn là, hãy chọn ra hai đoạn ~[x,y]~ ~(1 \le x \le y \le n)~ và ~[c,d]~ ~(1 \le c \le d \le n)~ sao cho ~S = \sum sum(i,j)~ với mọi ~x \le i \le y~ và ~c \le j \le d~ là lớn nhất.

Constraint

• ~1 \le n \le 400~.
• ~-10^6 \le b_i, a_i \le 10^6~.

Input

• Dòng đầu gồm số nguyên dương ~n~.
• Dòng thứ hai gồm ~n~ số nguyên miêu tả dãy ~a~.
• Dòng thứ ba gồm ~n~ số nguyên miêu tả dãy ~b~.

Output

• In ra ~S~ lớn nhất tìm được.

Subtask

• ~30\%~ số test có ~n \le 10~
• ~40\%~ số test có ~n \le 50~.
• ~30\%~ số test có ~n \le 400~.

Sample Input 1

5
1 4 2 -1 -2
-2 -1 1 2 -1

Sample Output 1

45

Explanation 1

• Chọn đoạn ~[1,5]~ và ~[2,5]~.

Bản đồ thành phố X có dạng lưới ô vuông ~M~ hàng ~N~ cột, các hàng được đánh số từ ~1~ tới ~M~, các cột được đánh số từ ~1~ tới ~N~. Mỗi ô vuông trên bản đồ có thể là khu đất trống hoặc một khu dân cư hoặc một siêu thị.

Mỗi siêu thị chỉ có thể phục vụ các khu dân cư có khoảng cách so với nó không quá ~D~, nghĩa là nếu siêu thị nằm ở ô ~(x, y)~ thì nó có thể phục vụ được tất cả các khu dân cư nằm trong hình vuông có ô trái trên là ~(x - D, y - D)~, ô phải dưới là ~(x + D, y + D)~ (như Hình 1).

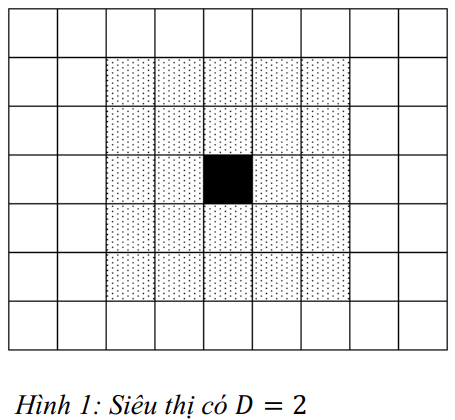
Một khu dân cư gọi là "chất lượng cao" nếu được ít nhất ~K~ siêu thị có thể phục vụ nó. Cho biết bản đồ của thành phố X, hãy đếm số lượng khu dân cư "chất lượng cao".

Dữ liệu vào từ file văn bản KHUDANCU.INP:

• Dòng đầu chứa bốn số nguyên ~M, N, D~ và ~K~ ~(1\le D \le \max(M, N); \ 1\le K\le M \times N)~;
• ~M~ dòng tiếp theo, mỗi dòng gồm ~N~ ký tự, mỗi ký tự biểu diễn một ô vuông bản đồ. Mỗi ký tự sẽ thuộc một trong ba loại sau:
  • . biểu diễn một khu đất trống;
  • P biểu diễn một khu dân cư;
  • M biểu diễn một siêu thị;

Dữ liệu đảm bảo tồn tại ít nhất một khu dân cư và ít nhất một siêu thị.

Kết quả ghi ra file văn bản KHUDANCU.OUT:

Ghi ra một số duy nhất là số khu dân cư "chất lượng cao".

Ví dụ

Input

5 5 1 2
P....
....P
..PM.
.M...
.....

Output

1

Giải thích

Bản đồ minh hoạ thành phố ~X~ như Hình 2.

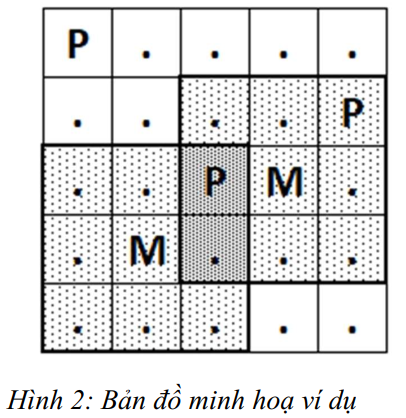
Khu dân cư ở ô ~(1, 1)~ không được siêu thị nào phục vụ;

Khu dân cư ở ô ~(2, 5)~ được một siêu thị có thể phục vụ;

Khu dân cư ở ô ~(3, 3)~ được hai siêu thị có thể phục vụ;

Vậy có một khu dân cư "chất lượng cao".

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thoả mãn: ~M = 1; \ N, D \le 10^3~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~M = 1; \ N \le 10^5~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~2 \le M, N \le 1000;~ số khu dân cư, số siêu thị không vượt quá ~1000~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài thoả mãn: ~2 \le M, N \le 1000~.

Nam được mẹ giao nhiệm vụ rèn luyện phép tính cộng cho em trai. Nam dự định vừa rèn luyện tính cộng vừa tạo niềm yêu thích tin học bằng cách cho em trai giải bài toán sau:

Cho một bảng số nguyên gồm có ~m~ hàng và ~n~ cột. Các hàng của bảng được đánh số từ ~1~ tới ~m~ từ trên xuông dưới, các cột của bảng số được đánh số từ ~1~ tới ~n~ từ trái qua phải. Giá trị của số nằm ở hàng ~i~ cột ~j~ được kí hiệu là ~a(i,j)~. Cần thực hiện lần lượt ~Q~ thao tác, thao tác thứ ~t~ ~(1 \le t \le Q)~ được mô tả bằng bộ năm số ~x_t,y_t,u_t,v_t,c_t~, thao tác này sẽ tăng tất cả các phần tử ~a(i,j)~ với mọi ~x_i \le i \le u_t, y_t \le j \le v_t~ lên một lượng là ~c_t~ ~(c_t > 0)~.

Nam sẽ yêu cầu em trai ghi ra giấy tất cả các phần tử của bảng số sau khi đã thực hiện cả ~Q~ thao tác. Để kiểm tra xem em mình làm có đúng không, Nam phải tự mình tính toán ra được kết quả đúng trước đã. Sau một hồi tính toán, Nam đã có được bảng số sau khi thực hiện ~Q~ thao tác. Tuy nhiên, giá trị của các phần tử của bảng số kết quả khá lớn! Nam sợ rằng em trai mình sẽ gặp khó khăn khi thực hiện phép cộng giữa hai số lớn, do đó Nam quyết định bỏ đi một thao tác sao cho sau khi thực hiện ~Q-1~ thao tác còn lại, giá trị lớn nhất của bảng số là nhỏ nhất có thể.

Yêu cầu: Cho bảng số và dãy ~Q~ thao tác, gọi ~W_t~ là giá trị lớn nhất trong bảng sau khi bỏ đi thao tác thứ ~t~ ~(1 \le t \le Q)~, tính ~Min(\{W_1,W_2,...,W_Q\})~.

Input

• Dòng đầu chứa hai số nguyên dương ~n,m~ .
• ~n~ dòng sau, dòng thứ ~i~ gồm ~n~ số nguyên không âm ~a(i,1), a(i,2), ..., a(i,n)~.
• Dòng tiếp theo chứa số nguyên dương ~Q~.
• Tiếp theo là ~Q~ dòng, dòng thứ ~t~ gồm ~5~ số nguyên dương ~x_t,y_t,u_t,v_t,c_t~.

Điều kiện

• ~1 \le n \times m \le 10^6~
• ~1 \le Q \le 10^6~
• ~a(i,j) \le 10^9~.
• ~c_i \le 10^3~.

Output

Gồm một dòng duy nhất là giá trị nhỏ nhất của giá trị lớn nhất của bảng số sau khi loại bỏ đi đúng một thao tác.

Ví dụ

Input

4 4
1 0 0 1
0 0 0 0
0 0 0 0
1 0 0 1
3
1 1 3 3 2
2 2 3 4 1
3 1 4 3 2

Output

3

Cấu trúc dữ liệu là nội dung rất quan trọng trong khoa học máy tính. Trong chương trình giảng dạy cho các lớp chuyên Tin, nội dung cấu trúc dữ liệu được đưa vào nhiều chuyên đề. Một bài toán thao tác trên bảng được dùng để kiểm tra khả năng tổ chức dữ liệu và linh hoạt trong xử lí như sau: Cho một bảng số gồm ~m~ hàng và ~n~ cột, các hàng được đánh số từ trên xuống dưới từ ~1~ đến ~m~, , các cột được đánh số từ trái sang phải từ ~1~ đến ~n~, ô nằm giao giữa hàng ~i~ ~(1 \le i \le m)~ và cột ~j~ ~(1 \le j \le n)~ gọi là ô ~(i,j)~ và có giá trị ban đầu là ~a_{i,j}~. Cần thực hiện ~Q~ thao tác trên bảng số, mỗi thao tác thuộc một trong hai loại:

• Thao tác loại ~1~ có dạng: ~1~ ~x~ ~y~ ~u~ ~v~ ~w~ có nghĩa là với mỗi ô nằm trong hình chữ nhật có ô trái trên là ô ~(x,y)~ và ô phải dưới là ô ~(u,v)~ sẽ được cộng thêm ~w~.
• Thao tác loại ~2~ có dạng: ~2~ ~x~ ~y~ ~u~ ~v~ có nghĩa là cần đưa ra tổng giá trị của các ô nằm trong hình chữ nhật có ô trái trên là ô ~(x,y)~ và ô phải dưới là ô ~(u,v)~.

Input

• Dòng đầu tiên chứa ba số nguyên dương ~m,n,Q~ ~ (1 \le m,n \le 500)~.
• Dòng thứ ~i~ ~(1 \le i \le m)~ trong ~m~ dòng sau chứa ~n~ số nguyên không âm ~a_{i,1},a_{i,2},...,a_{i,n}~ ~(a_{i,j} \le 10^9)~.
• Dòng thứ ~k~ ~(1 \le k \le Q)~ trong ~Q~ dòng sau mô tả thao tác thứ ~k~:
  • Nếu là thao tác loại ~1~, gồm một dòng sáu số nguyên ~1,x,y,u,v,w~ ~(1 \le x \le u \le m; 1 \le y \le v \le n; 0 \le w \le 10^9)~
  • Nếu là thao tác loại ~2~, gồm một dòng năm số nguyên ~2,x,y,u,v~ ~(1 \le x \le u \le m; 1 \le y \le v \le n)~

Output

• Với mỗi truy vấn loại ~2~, in ra kết quả truy vấn đó.

Subtask

• ~30\%~ số điểm: ~Q \le 100~
• ~30\%~ số điểm: ~Q \le 10^5~ và tất cả thao tác loại ~1~ xuất hiện trước thao tác loại ~2~.
• ~20\%~ số điểm: ~Q \le 10^4~
• ~20\%~ số điểm: ~Q \le 10^5~

Ví dụ

Input 1:

2 3 3
0 0 0
0 0 0
2 1 1 2 3
1 1 1 2 3 1
2 1 1 2 2      

Output 1:

0
4