Bể nước
Nộp bàiPoint: 100
MrTee muốn xây một bể cá để lấy thịt chiêu đãi học sinh. Sẵn tiện được cho ~1~ rặng san hô gồm ~N~ cột, mỗi cột có độ cao là ~a_{i}~, MrTee muốn xây bể cá như sau:
- Chọn một số nguyên dương ~h~ là độ cao của thành bể để dựng ~2~ bên bể.
- Sau đó, đổ nước vào bể sao cho mọi cột và nước đều cao bằng ~h~, với cột san hô nào có độ cao ~> h~ thì không đổ thêm nước vào nữa.
Ví dụ: ~a=[3,1,2,4,6,2,5], h=4~
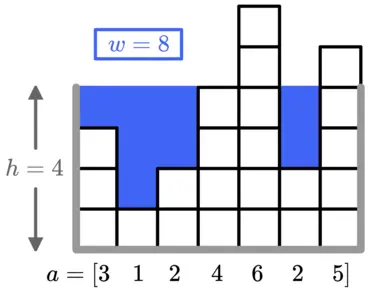
Tuy nhiên, hóa đơn tiền nước rất đắt đỏ và MrTee chỉ muốn bỏ tiền ra cho ~x~ ô nước. Giá trị ~h~ lớn nhất mà MrTee có thể chọn là bao nhiêu?
INPUT
- Dòng đầu tiên là ~1~ số nguyên dương ~t~ là số test ~(1 \leq t \leq 10^4)~.
- Dòng đầu tiên của mỗi test case là ~2~ số ~n, x~ đại diện cho số cột san hô và số lượng nước cho phép (~1 \leq x \leq 10^9~).
- Dòng thứ ~2~ của mỗi test case là ~n~ số ~a_{i}~ là độ cao mỗi cột san hô. (~1 \leq a[i] \leq 10^9~)
- Tổng giá trị của ~n~ trong mọi test không vượt quá ~2 \times 10^5~.
OUTPUT
- Mỗi test case ~1~ dòng là độ cao ~h~ lớn nhất thỏa mãn.
SAMPLE TEST
Input:
5
7 9
3 1 2 4 6 2 5
3 10
1 1 1
4 1
1 4 3 4
6 1984
2 6 5 9 1 8
1 1000000000
1
Output:
4
4
2
335
1000000001
Goodtopic
Nộp bàiPoint: 100
Bài học tiếp theo tại lớp học thuật toán của sẽ học về hai chủ đề. Chủ đề thứ ~i~ có mức độ hấp dẫn ~a_i~ đơn vị với giáo viên và ~b_i~ đơn vị với học sinh. Một cặp chủ đề ~i~ và ~j~ (~i < j~) được gọi là tốt nếu ~a_i + a_j > b_i + b_j~ (tức là nó hấp dẫn hơn cho giáo viên).
Yêu cầu: Hãy tìm số lượng các cặp chủ đề tốt như vậy.
Input
- Dòng đầu tiên chứa một số nguyên ~n~ (~2 \leq n \leq 2 \times 10^5~) là số lượng chủ đề;
- Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~1 \leq a_i \leq 10^9~), trong đó ~a_i~ là mức độ hấp dẫn của chủ đề thứ ~i~ đối với giáo viên;
- Dòng thứ ba chứa ~n~ số nguyên ~b_1, b_2, \ldots, b_n~ (~1 \leq b_i \leq 10^9~), trong đó ~b_i~ là mức độ hấp dẫn của chủ đề thứ ~i~ đối với học sinh.
Output
Đối với mỗi test case, ghi ra một số nguyên duy nhất là số lượng cặp thỏa mãn tìm được.
Sample Test
Input:
5
4 8 2 6 2
4 5 4 1 3
Output:
7
Array Division
Nộp bàiPoint: 100
Bạn được cho một mảng chứa ~n~ số nguyên dương.
Nhiệm vụ của bạn là chia mảng thành ~k~ đoạn con sao cho tổng lớn nhất trong một đoạn con là nhỏ nhất có thể.
Input
- Dòng đầu tiên của đầu vào chứa hai số nguyên ~n~ và ~k~ - kích thước của mảng và số đoạn con cần chia.
- Dòng tiếp theo chứa ~n~ số nguyên ~x_1, x_2, \dots, x_n~ - các phần tử của mảng.
Output
- In ra một số nguyên: tổng lớn nhất trong một đoạn con trong cách chia tối ưu.
Constraints
- ~1 \leq n \leq 2\times10^5~
- ~1 \leq k \leq n~
- ~1 \leq x_i \leq 10^9~
Sample Test
Input:
5 3
2 4 7 3 5
Output:
8
Vanya and Lanterns
Nộp bàiPoint: 100
Vanya đi bộ vào buổi đêm trên một con đường thẳng độ dài ~l~, được soi sáng bởi ~n~ đèn lồng. Xét hệ tọa độ với đầu đường tương ứng với điểm ~0~, và cuối đường tương ứng với điểm ~l~. Khi đó đèn lồng thứ ~i~ ở điểm ~a_i~. Đèn lồng soi sáng tất cả các điểm trên đường có khoảng cách tới nó không vượt quá ~d~, với ~d~ là một số dương, giống nhau với tất cả đèn lồng.
Vanya thắc mắc: Bán kính ánh sáng ~d~ nhỏ nhất là bao nhiêu để các đèn lồng có thể soi sáng toàn bộ con đường?
Input
- Dòng đầu tiên gồm hai số nguyên ~n, l~ (~1 \le n \le 1000, 1 \le l \le 10^9~) - số lượng đèn lồng và độ dài con đường.
- Dòng tiếp theo gồm ~n~ số nguyên ~a_i~ (~0 \le a_i \le l~). Nhiều đèn lồng có thể được đặt tại cùng một điểm. Các đèn lồng có thể được đặt ở hai đầu đường.
Output
In ra bán kính ánh sáng nhỏ nhất ~d~ cần để soi sáng toàn bộ đường. Câu trả lời được coi là đúng nếu chênh lệch không vượt quá ~10^{-9}~.
Sample test:
Input 1:
7 15
15 5 3 7 9 14 0
Output 1:
2.5000000000
Input 2:
2 5
2 5
Output 2:
2.0000000000
Note
Xét ví dụ thứ hai. Với ~d = 2~ đèn lồng đầu tiên sẽ soi sáng đoạn ~[0, 4]~ của con đường, và đèn lồng thứ hai sẽ soi sáng đoạn ~[3, 5]~ . Do đó, cả con đường sẽ được soi sáng.
Sheokand and Number
Nộp bàiPoint: 100
Sheokand rất giỏi toán học. Một ngày nọ, để kiểm tra kỹ năng toán của cậu ấy, Kaali đưa cho cậu ấy một số nguyên ~N~.
Vì muốn gây ấn tượng tốt, Sheokand cần chuyển ~N~ thành số nguyên ~M~ có thể biểu diễn dưới dạng ~2^x + 2^y~ (trong đó ~x~ và ~y~ là các số nguyên không âm sao cho ~x \neq y~). Để làm điều đó, cậu ấy có thể thực hiện hai loại thao tác:
- Cộng ~1~ vào ~N~
- Trừ ~1~ khỏi ~N~
Tuy nhiên, Sheokand đang chuẩn bị cho kỳ thi của mình. Bạn có thể giúp cậu ấy tìm số thao tác tối thiểu cần thiết để chuyển ~N~ thành một số nguyên hợp lệ ~M~ không?
Input
- Dòng đầu tiên của đầu vào chứa một số nguyên ~T~ (~1 \leq T \leq 10^5~) - biểu thị số lượng các trường hợp thử nghiệm. Phần mô tả của ~T~ trường hợp thử nghiệm tiếp theo.
- Dòng đầu tiên và duy nhất của mỗi trường hợp thử nghiệm chứa một số nguyên ~N~ (~1 \leq N \leq 10^9~).
Output
Đối với mỗi trường hợp thử nghiệm, in ra một dòng chứa một số nguyên - số thao tác tối thiểu cần thiết.
Sample Test
Input:
3
10
22
4
Output:
0
2
1
Factory Machines
Nộp bàiPoint: 100
Một nhà máy có ~n~ máy có thể được sử dụng để sản xuất sản phẩm. Mục tiêu của bạn là sản xuất tổng cộng ~t~ sản phẩm.
Với mỗi máy, bạn biết thời gian mà nó cần để sản xuất một sản phẩm. Các máy có thể hoạt động đồng thời, và bạn có thể tự do sắp xếp lịch làm việc của chúng.
Hỏi thời gian ngắn nhất cần thiết để sản xuất ~t~ sản phẩm là bao lâu?
Input
- Dòng đầu tiên của đầu vào chứa hai số nguyên ~n~ và ~t~ - số lượng máy móc và số sản phẩm cần sản xuất.
- Dòng tiếp theo chứa ~n~ số nguyên ~k_1, k_2, \dots, k_n~ - thời gian cần để một máy sản xuất ra một sản phẩm.
Output
In ra một số nguyên duy nhất: thời gian ít nhất để sản xuất ~t~ sản phẩm?
Constraints
- ~1 \leq n \leq 2 \times 10^5~
- ~1 \leq t \leq 10^9~
- ~1 \leq k_i \leq 10^9~
Sample Test
Input:
3 7
3 2 5
Output:
8
Diệt rồng
Nộp bàiPoint: 100
Tôm đang chơi một trò chơi máy tính khác. Trong trò chơi này, nhân vật của anh ta phải tiêu diệt một con rồng. Trận chiến với con rồng kéo dài ~100^{500}~ giây, trong đó Tôm tấn công con rồng bằng một con dao găm tẩm độc.
Lần tấn công thứ ~i~ được thực hiện vào giây thứ ~a_i~ tính từ khi trận chiến bắt đầu. Con dao găm không gây sát thương trực tiếp, nhưng nó áp dụng hiệu ứng độc lên con rồng. Hiệu ứng độc này gây ~1~ sát thương trong mỗi giây tiếp theo, kéo dài ~k~ giây (bắt đầu ngay từ giây mà con dao găm đâm vào con rồng). Tuy nhiên, nếu con rồng đã bị dính độc trước đó, hiệu ứng độc sẽ được làm mới (tức là hiệu ứng hiện tại bị hủy và hiệu ứng mới được áp dụng).
Ví dụ, giả sử ~k = 4~, và Tôm đâm con rồng vào các giây thứ ~2, 4~ và ~10~. Hiệu ứng độc sẽ được áp dụng bắt đầu từ giây thứ ~2~ và gây ~1~ sát thương trong các giây 2 và 3; sau đó, vào đầu giây thứ ~4~, hiệu ứng độc được làm mới, vì vậy nó gây ~1~ sát thương trong các giây ~4, 5, 6~ và ~7~; cuối cùng, vào giây thứ ~10~, hiệu ứng độc được áp dụng lại, gây ~1~ sát thương trong các giây ~10, 11, 12~ và ~13~. Tổng cộng, con rồng nhận ~10~ sát thương.
Tôm biết rằng con rồng có ~h~ máu, và nếu anh ta gây ít nhất ~h~ sát thương cho con rồng trong trận chiến, anh ta sẽ tiêu diệt được nó. Tôm chưa quyết định hiệu lực của chất độc mà anh ta sẽ sử dụng trong trận chiến, vì vậy anh ta muốn tìm giá trị nhỏ nhất của ~k~ (số giây mà hiệu ứng độc kéo dài) đủ để gây ít nhất ~h~ sát thương cho con rồng.
Input
- Dòng đầu tiên chứa số nguyên t (~1 \leq t \leq 1000~) - số lượng test cases.
- Dòng đầu tiên của mỗi test case chứa ~2~ số nguyên ~n~ và ~h~ (~1 \leq n \leq 100, 1 \leq h \leq 10^{18}~) - số đòn tấn công và số sát thương phải gây ra cho rồng.
- Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \dots a_n~ (~1 \leq a_i \leq 10^9, a_i < a_{i + 1}~) - ~a_i~ là thời gian mà đòn tấn công thứ ~i~ được thực hiện.
Output
- Với mỗi tese case, in ra một số nguyên - số ~k~ bé nhất để Tôm gây ra ít nhất ~h~ sát thương cho con rồng.
Sample test
Input:
4
2 5
1 5
3 10
2 4 10
5 3
1 2 4 5 7
4 1000
3 25 64 1337
Output:
3
4
1
470
Note
- Trong ví dụ đầu tiên, với ~k = 3~, sát thương được gây ra vào các giây ~[1, 2, 3, 5, 6, 7]~.
- Trong ví dụ thứ hai, với ~k = 4~, sát thương được gây ra vào các giây ~[2, 3, 4, 5, 6, 7, 10, 11, 12, 13]~.
- Trong ví dụ thứ ba, với ~k = 1~, sát thương được gây ra vào các giây ~[1, 2, 4, 5, 7]~.
Đường ống nước
Nộp bàiPoint: 100
Tôm muốn xây dựng một hệ thống ống dẫn nước. Vì có chính xác ~n~ ngôi nhà nên Tôm muốn thành phố có chính xác ~n~ ống nước, mỗi ống này phải được kết nối với nguồn nước. Một ống có thể được kết nối với nguồn nước nếu có nước chảy ra từ nó. Ban đầu, Tôm chỉ có một ống có nước chảy qua. Ngoài ra, Tôm còn có một số bộ chia.
Một bộ chia gồm ~1~ đầu vào (có thể được kết nối với một ống nước khác) và ~x~ đầu ra. Khi một bộ chia được kết nối với một ống nước, nước sẽ chảy ra từ mỗi đầu ra. Có thể coi rằng các ống đầu ra này giống như các ống nước bình thường. Ví dụ, bạn có thể kết nối chúng với nguồn nước nếu có nước chảy qua. Mỗi ống nước chỉ có thể kết nối với tối đa một bộ chia.
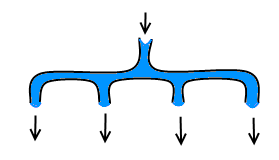
Tôm có một bộ chia của mỗi loại: với ~2, 3, 4, \dots, k~ đầu ra. Hãy giúp Tôm sử dụng số lượng bộ chia ít nhất để xây dựng hệ thống ống dẫn như yêu cầu, hoặc xác định rằng điều này là không thể.
Tôm cần hệ thống ống nước có chính xác ~n~ ống với nước chảy ra. Lưu ý rằng một số ống này có thể là đầu ra của các bộ chia.
Input
- Đầu vào chứa duy nhất hai số nguyên cách nhau bởi khoảng trắng ~n~ và ~k~ (~1 \leq n \leq 10^{18}, 2 \leq k \leq 10^9~).
Lưu ý: Đừng sử dụng định dạng %lld để đọc hoặc ghi số nguyên 64-bit trong C++. Thay vào đó, nên sử dụng luồng cin, cout hoặc định dạng %I64d.
Output
In ra một số nguyên duy nhất - số lượng bộ chia tối thiểu cần thiết để xây dựng hệ thống ống nước. Nếu không thể xây dựng hệ thống với các bộ chia đã cho, in ra -1.
Sample Test
| Input | Output |
|---|---|
| 4 3 | 2 |
| 5 5 | 1 |
| 8 4 | -1 |
Get the Containers
Nộp bàiPoint: 100
Một băng chuyền có một số thùng chứa có dung tích khác nhau, mỗi thùng đều chứa đầy sữa. Sữa từ băng chuyền sẽ được rót vào ~m~ thùng rỗng, thỏa mãn các điều kiện sau:
- Khi sữa được đổ vào một thùng rỗng, sữa trong thùng chứa phải được đổ hoàn toàn vào thùng rỗng đó. Tức là, sữa từ cùng một thùng chứa không thể được đổ vào nhiều thùng rỗng khác nhau.
- Sữa từ các thùng chứa phải được đổ vào thùng rỗng theo thứ tự mà chúng xuất hiện trên băng chuyền. Tức là, bạn không thể chọn ngẫu nhiên một thùng chứa trên băng chuyền để đổ vào thùng.
- Thùng chứa thứ ~i~ chỉ được đổ sữa từ các thùng chứa xuất hiện trước những thùng chứa đổ vào thùng thứ ~j~, với mọi ~i < j~.
Với số thùng chứa là ~m~, bạn phải đổ sữa từ tất cả các thùng chứa vào các thùng, không để lại sữa trong thùng chứa nào. Các thùng chứa không nhất thiết phải có cùng dung tích. Bạn có thể tự do gán bất kỳ dung tích nào cho chúng. Công việc của bạn là tìm ra dung tích tối thiểu có thể của thùng chứa có dung tích lớn nhất.
Input
- Dòng đầu tiên chứa duy nhất số nguyên ~T~ (~T \leq 100~) - số lượng bộ test.
- Mỗi bộ test chứa ~2~ số nguyên dương ~n~ và ~m~ (~1 \leq n \leq 1000~, ~1 \leq m \leq 10^6~) - số lượng thùng trên băng chuyền và số lượng thùng cần chuyển sữa vào.
- Dòng tiếp theo chứa ~n~ số nguyên dương ~c_i~ (~1 \leq c \leq 10^6~) - dung tích của mỗi thùng. Lưu ý rằng, sữa được đổ đầy đến miệng của mỗi thùng chứa, vì vậy dung tích của thùng chứa cũng chính là lượng sữa trong đó.
Output
Với mỗi truy vấn thứ ~i~, in ra kết quả thỏa mãn.
Sample Test
Input:
2
5 3
1 2 3 4 5
3 2
4 78 9
Output:
6
82
Dãn cách đàn bò
Nộp bàiPoint: 100
Tôm đang rất lo lắng cho đàn bò của mình do dịch bệnh COWVID-19. Để giảm thiểu sự lây nhiễm của bệnh, ~n~ con bò của Tôm đã thực hiện "dãn cách xã hội" và trải đều ra khắp trang trại.
Trang trại có hình dạng như một đường thẳng, với ~m~ bãi cỏ cho bò ăn có thể giao nhau. Mỗi con bò muốn đứng ở một điểm khác nhau mà ở đó có cỏ để có được ~D~ lớn nhất, với ~D~ là khoảng cách gần nhất giữa các cặp bò. Hãy tìm ~D~ lớn nhất có thể.
Input
- Dòng thứ nhất chưa hai số nguyên ~n~ và ~m~ (~1 \leq n, m \leq 10^5~)
- ~m~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~a~ và ~b~ là điểm đầu và điểm cuối của bãi cỏ, biết các bãi cỏ không giao nhau (~1 \leq a, b \leq 10^{18}~)
Output
In ra ~D~ lớn nhất, trong đó tất cả các con bò cách nhau ít nhất khoảng cách là ~D~.
Sample Test
Input:
5 3
0 2
4 7
9 9
Output:
2
Một cách khả thi với ~D = 2~ là bò ở các vị trí ~0, 2, 4, 6, 9~