Cho hai số nguyên dương ~a~, ~n~. Tính ~a^n~.

Input

Gồm một dòng chứa hai số nguyên dương ~a~, ~n~. (~a, n \leq 20~)

Dữ liệu đảm bảo ~a^n~ luôn nhỏ hơn ~10^{19}~.

Output

In ra giá trị ~a^n~.

Sample Test

Input:

2 3

Output:

8

Cho hai số nguyên dương ~a~ và ~b~. Hãy tìm ước chung lớn nhất và bội chung nhỏ nhất của hai số đó.

Input

Gồm một dòng chứa hai số nguyên dương ~a~ và ~b~. (~a, b \leq 10^6~)

Output

Gồm hai dòng, dòng đầu tiên chứa ước chung lớn nhất và dòng thứ hai chứa bội chung nhỏ nhất của ~a~ và ~b~.

Sample Test

Input:

2
5

Output

1
10

Bạn được nhận ~n~ xâu kí tự, mỗi xâu gồm các chữ cái tiếng Anh in thường. Cần chọn ra một số xâu trong ~n~ xâu đó sao cho khi ghép tất cả chúng lại, ta được một xâu mới bao gồm đầy đủ các kí tự trong bảng chữ cái tiếng Anh. Hãy đếm số cách để thực hiện yêu cầu trên. Hai cách được coi là khác nhau khi có một xâu được chọn ở cách này không được chọn trong cách kia.

Input

• Dòng đầu tiên gồm số nguyên dương ~n~ ~(n \le 25)~ miêu tả số lượng xâu.
• ~n~ dòng tiếp theo, mỗi dòng bao gồm một xâu kí tự ~S~ ~(|S| \le 30)~ gồm các chữ cái tiếng Anh in thường.

Output

• In ra một số nguyên là kết quả bài toán.

Sample Test

Input1:

8
the
quick
brown
fox
jumps
over
lazy
dog

Output1:

1

Input2:

3
a
b
abcdefghijklmnopqrstuvwxyz

Output2:

4

Cho dãy số gồm ~n~ số nguyên ~c_1, c_2, …, c_n~ và số nguyên dương ~m~. Nhiệm vụ của bạn là tìm một đoạn ~b_1,b_2,...,b_k~ ~(1 \le b_1 < b_2 < ... < b_k \le n)~ sao cho ~(\sum c_{b_i}) \% m~ là lớn nhất có thể. Đoạn con tìm được có thể rỗng.

Yêu cầu: Hãy in ra giá trị lớn nhất tìm được.

Input

• Dòng đầu tiên chứa ~2~ số nguyên duyên ~n,m~
• Dòng thứ hai chứa dãy ~c~ gồm ~n~ phần tử.

Output

• Một số nguyên duy nhất là giá trị lớn nhất tìm được.

Constraints

• ~1 \le n \le 40~
• ~1 \le m \le 10^9~
• ~1 \le c_i \le 10^9~

Subtask

• Có ~50\%~ số test ứng với ~n \le 20~.
• Có ~50\%~ số test ứng với ~n \le 40~.

Sample Input 1

4 4
5 2 4 1

Sample Output 1

3

Sample Input 2

3 20
199 41 299

Sample Output 2

19

Với hai số nguyên dương ~u,v~, khi viết số ~v~ sau số ~u~ ta được một số mới.

Ví dụ: ~u = 99, v = 123~, khi viết số ~v~ sau ~u~ ta thu được số mới là số ~99123~.

Cho ~n~ số nguyên dương ~a_1, a_2, a_3, ... a_n~ và ~m~ số nguyên dương ~b_1, b_2, b_3, ..., b_m~.

Yêu cầu:

• Với mỗi giá trị ~b_i~ ~(1 \le i \le m)~, bạn hãy cho biết có bao nhiêu số ~a_j~ (~1 \le j \le n~) sao cho sau khi viết ~a_j~ sau ~b_i~ ta được một số mới chia hết cho ~3~.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~n,m~. (~1 \le n,m \le 10^5~).
• Dòng tiếp theo chứa ~n~ số nguyên dương miêu tả dãy ~a~. (~a_i \le 10^8, 1 \le i \le n~).
• Dòng tiếp theo chứa ~m~ số nguyên dương miêu tả dãy ~b~. (~b_i \le 10^8, 1 \le i \le m~).

Output

• Gồm ~m~ dòng, dòng thứ ~i~ ghi số lượng số ~a_j (1 \le j \le n)~ sao cho sau khi viết ~a_j~ sau ~b_i~ ta được một số mới chia hết cho ~3~.

Subtask

• Subtask ~1~ (~60\%~ số điểm): ~n,m \le 1000~
• Subtask ~2~ (~40\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

5  2
123  4  5  7  10
3  2

Sample Output 1

1
3

Explanation 1

~b_1 = 3~ chỉ có duy nhất một số ~a_1~ thỏa mãn. ~b_2 = 2~, có ba số ~a_2,a_4,a_5~ thỏa mãn.

Sinh xâu nhị phân độ dài ~n~.

Yêu cầu: Cho ~n~ hẫy in tất cả các xâu nhị phân theo thứ tự từ điển.

Input

• Số nguyên dương ~n (n \leq 12)~.

Output

• Tất cả các xâu nhị phân theo thứ tự từ điển.

Sample Tests

Input

3 

Output

000
001
010
011
100
101
110
111

Cho ~2~ mảng ~a~ và ~b~ đều gồm ~n~ số nguyên dương và một số nguyên dương ~k~. Mảng số nguyên ~c~ gồm ~n^2~ phần tử được xây dựng bằng cách với mỗi cặp ~i,j~ thỏa mãn ~1 \le i,j \le n~, ta gán giá trị ~c_{(i-1)*n+j} = a_i + b_j~.

Sắp xếp mảng ~c~ lại theo thứ tự không giảm, hãy in ra số thứ ~k~ trong dãy ~c~ mới.

Input

• Dòng đầu gồm ~2~ số nguyên dương ~n~ và ~k~.
• Dòng tiếp theo gồm ~n~ số nguyên dương mô tả dãy ~a~.
• Dòng cuối cùng gồm ~n~ số nguyên dương mô tả dãy ~b~.

Output

• In ra kết quả của bài toán.

Constraints

• ~1 \le n \le 10^5~, ~1 \le k \le n^2~.
• ~1 \le a_i,b_i \le 10^9~.

Subtask

• ~50\%~ số điểm có ~n \le 1000~.
• ~50\%~ còn lại không có giới hạn gì thêm.

Sample Input 1

5 10
4 2 6 4 8
7 3 1 9 5

Sample Output 1

9

Cho hai dãy ~a~ và ~b~ cùng có ~n~ phần tử nguyên. Ta định nghĩa hàm ~sum(x,y)~ ~(1 \le x,y \le n)~ như sau:

• Nếu ~x \le y~ thì ~sum(x,y) = a_x + a_{x+1} + a_{x+2} + ... + a_y~.
• Nếu ~x > y~ thì ~sum(x,y) = b_x + b_{x-1} + b_{x-2} + ... + b_y~.

Nhiệm vụ của bạn là, hãy chọn ra hai đoạn ~[x,y]~ ~(1 \le x \le y \le n)~ và ~[c,d]~ ~(1 \le c \le d \le n)~ sao cho ~S = \sum sum(i,j)~ với mọi ~x \le i \le y~ và ~c \le j \le d~ là lớn nhất.

Constraint

• ~1 \le n \le 400~.
• ~-10^6 \le b_i, a_i \le 10^6~.

Input

• Dòng đầu gồm số nguyên dương ~n~.
• Dòng thứ hai gồm ~n~ số nguyên miêu tả dãy ~a~.
• Dòng thứ ba gồm ~n~ số nguyên miêu tả dãy ~b~.

Output

• In ra ~S~ lớn nhất tìm được.

Subtask

• ~30\%~ số test có ~n \le 10~
• ~40\%~ số test có ~n \le 50~.
• ~30\%~ số test có ~n \le 400~.

Sample Input 1

5
1 4 2 -1 -2
-2 -1 1 2 -1

Sample Output 1

45

Explanation 1

• Chọn đoạn ~[1,5]~ và ~[2,5]~.

Cho một dãy ~a~ gồm ~n~ phần tử nguyên dương và một số nguyên dương ~k~.

Ta có định nghĩa như sau:

• ~MaxSecond(l,r) :~ phần tử lớn thứ hai trong đoạn ~[l,r]~ của dãy ~a~.
• ~MinSecond(l,r) :~ phần tử nhỏ thứ hai trong đoạn ~[l,r]~ của dãy ~a~.
• ~f(l,r) = MaxSecond(l,r) - MinSecond(l,r)~

Hãy tìm một đoạn con ~[l,r]~ dài nhất sao cho ~f(l,r) \le k~.

Input

• Dòng thứ nhất chứa ~2~ số nguyên dương: ~n,k~.
• Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy ~a~.

Output

• In ra số ~X~ là độ dài của đoạn con dài nhất thỏa mãn. Dữ liệu đảm bảo luôn tồn tại kết quả.

Constraints

• ~1 \le n \le 10^5~.
• ~1 \le a_i \le 10^9~.
• ~1 \le k \le 10^9~.

Subtasks

• Subtask ~1~: ~n \le 1000~ ~(50\%)~
• Subtask ~2~: Không có ràng buộc gì thêm ~(50\%)~

Sample Input 1:

5 2
1 4 2 6 5

Sample Output 1:

4

Explanation 1:

Chọn đoạn ~[1,4]~.

Sample Input 2:

7 3
9 1 4 3 12 16 8

Sample Output 2:

4

Explanation 2:

Chọn đoạn ~[2,5]~.

Đất nước Mirinda tươi đẹp được mô tả bằng một ma trận ~n \times m~ ô vuông, ô ở dòng thứ ~i~ từ trên xuống và cột thứ ~j~ từ trái sang gọi là ô ~(i, j)~. Khoảng cách giữa ô ~(x,y)~ với ô ~(i,j)~ là ~|x - i| + |y - j|~. Ô ~(i, j)~ có giá trị tài sản là ~a_{i,j}~.

Do biến đổi khí hậu, những cơn bão ngày một nhiều hơn và mạnh hơn. Mỗi cơn bão được đặc trưng bởi:

• ~w~ - cấp bão,
• ~R_1~ - bán kính bão,
• ~R_2~ - bán kính mắt bão,
• ~(x, y)~ - tọa độ bão sẽ đổ bộ.

Theo đó, các ô ~(i, j)~ có khoảng cách đến ô ~(x, y)~ thuộc đoạn ~[R_2, R_1]~ sẽ bị tác động, đồng thời giá trị tài sản ở ô đó sẽ giảm đi min(w, b[i][j]), với ~b_{i,j}~ là giá trị tài sản hiện có ở ô ~(i, j)~.

Là một nước giáp biển, hằng năm đất nước Mirinda phải đón ~k~ trận bão. Do đặc trưng địa hình, bão sẽ chỉ đổ bộ vào một trong ~q~ ~(q < 5)~ điểm phân biệt. Rút kinh nghiệm từ siêu bão Fanta, ủy ban chống bão muốn biết sau khi ~k~ trận bão đó tàn phá thì nước này phải chịu tổng thiệt hại là bao nhiêu?

(Tổng thiệt hại của nước này được tính bằng tổng mức giảm giá trị tài sản của tất cả các ô).

Input

• Dòng đầu tiên chứa ~4~ số nguyên dương ~n,m,q,k~ (~1 < n, m < 500, k \leq 10^5~).
• ~n~ dòng tiếp theo, mỗi dòng chứa ~m~ số nguyên ~a_{i,j}~ (~0 < a_{i,j} < 10^9~).
• Dòng tiếp theo ghi ~2 \times q~ số nguyên là tọa độ của ~q~ điểm đặc biệt: ~x_1, y_1, x_2, y_2, \ldots, x_q, y_q~.
• ~k~ dòng cuối, mỗi dòng ghi ~5~ số nguyên mô tả cơn bão: ~w, R_1, R_2, x, y~ (~0 < R_2 < R_1 < 1000, 0 < w < 1000~). Dữ liệu đảm bảo ~x,y~ là ~1~ trong ~q~ điểm đã cho.

(Các trận bão sẽ được liệt kê theo đúng thứ tự đổ bộ).

Output

In ra tổng thiệt hại sau ~k~ cơn bão.

Sample Test

Input:

3 4 2 4
10 11 12 15
20 10 11 25
30 32 35 40
1 1 3 4
2 2 0 3 4
2 2 0 1 1
2 4 2 1 1
2 3 1 3 4

Output:

56

Thao tác tăng hình nón đối xứng của một dãy số ~X_1,X_2,X_3,…,X_{N-2},X_{N-1},X_N~ được thực hiện như sau:

• Tăng ~X_1~ và ~X_N~ lên ~1~ đơn vị~;~
• Tăng ~X_2~ và ~X_{N-1}~ lên ~2~ đơn vị~;~
• Tăng ~X_3~ và ~X_{N-2}~ lên ~3~ đơn vị~;~
• ~…~

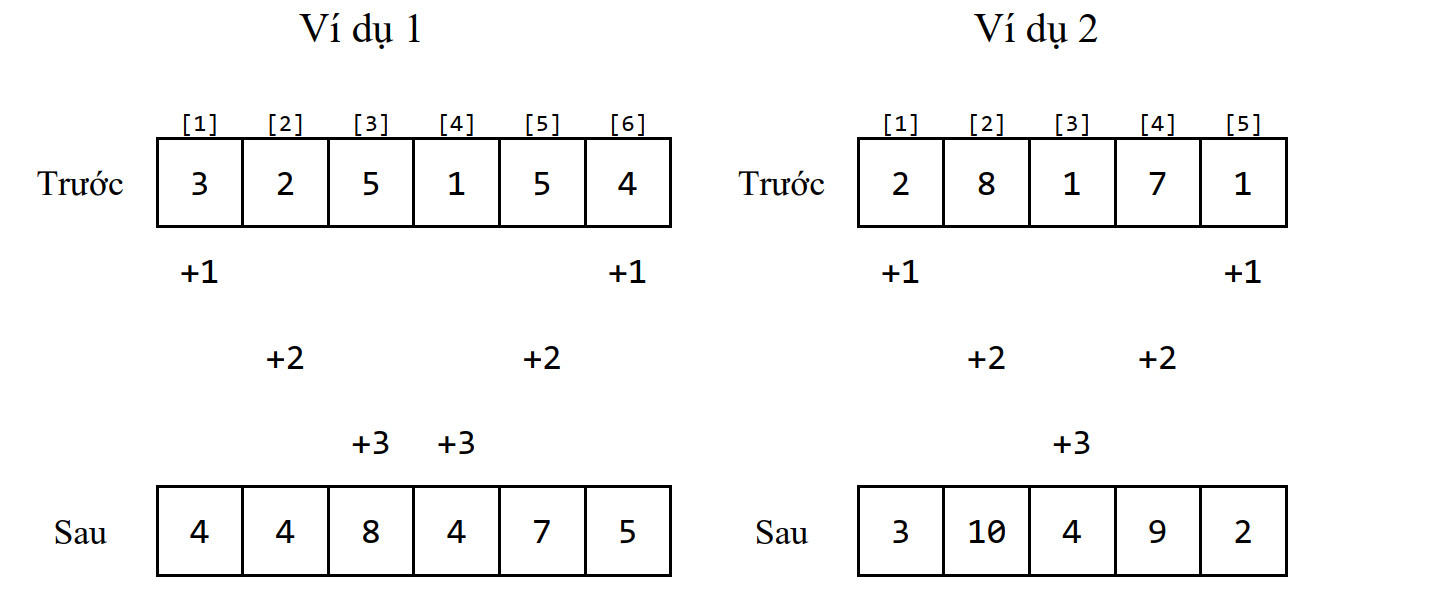
Cho một bảng hình vuông ~A~ có ~N~ dòng, ~N~ cột. Các dòng được đánh số từ ~1~ tới ~N~ theo thứ tự từ trên xuống dưới và các cột được đánh số từ ~1~ tới ~N~ theo thứ tự từ trái qua phải. Ô ở dòng thứ ~i~, cột thứ ~j~ được gọi là ô ~A(i,j)~. Ban đầu tất cả các ô đều có giá trị bằng ~0~. Thực hiện ~T~ thao tác tăng hình nón đối xứng trên bảng ~A~, mỗi thao tác có cấu trúc như sau: gồm bốn số nguyên dương ~k,rc,x,y~ ~(k=1~ hoặc ~k=2)~ có ý nghĩa:

• Khi ~k = 1,~ thực hiện tăng hình nón đối xứng trên dòng ~rc~ với dãy số gồm các số từ ~A(rc,x)~ đến ~A(rc,y);~
• Khi ~k = 2,~ thực hiện tăng hình nón đối xứng trên cột ~rc~ với dãy số gồm các số từ ~A(x,rc)~ đến ~A(y,rc)~.

Yêu cầu: Cho kích thước bảng, ~T~ thao tác tăng và ~Q~ câu hỏi. Mỗi câu hỏi có ý nghĩa: tìm giá trị của một ô của bảng sau khi thực hiện ~T~ thao tác.

Dữ liệu nhập vào từ file văn bản ITABLE.INP:

• Dòng đầu tiên gồm hai số nguyên dương ~N~ và ~T~ là kích thước của bảng và số thao tác tăng. ~(N≤5000; \ T≤10^5)~
• ~T~ dòng sau, mỗi dòng gồm bốn số nguyên dương ~k,rc,x,y~ mô tả thao tác tăng lên dòng hoặc cột của bảng. ~(k=1~ hoặc ~k=2; \ rc,x,y≤N)~
• Dòng tiếp theo gồm số một số nguyên dương ~Q~ là số ô cần tìm giá trị. ~(Q≤10^5)~
• ~Q~ dòng sau, mỗi dòng chứa hai số nguyên dương ~u,v~ có ý nghĩa là cần tìm giá trị của ô ~A(u,v)~. ~(u,v≤N)~

Mỗi số cách nhau một dấu cách. Dữ liệu đảm bảo đúng đắn và luôn có kết quả.

Kết quả ghi ra file văn bản ITABLE.OUT:

Gồm ~Q~ dòng, mỗi dòng in ra giá trị của một ô tương ứng.

Ví dụ

Input

4 2
1 2 1 4
2 3 1 3
3
1 1
2 2
2 3

Output

0
2
4

Giải thích:

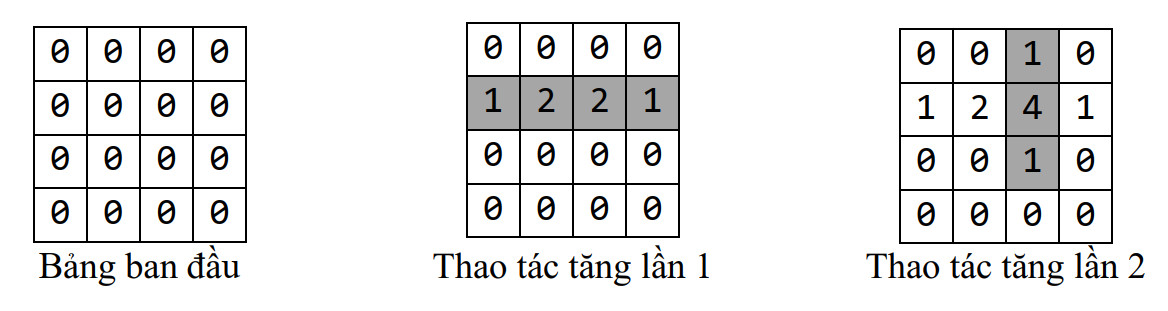
Giới hạn

• Có ~50\%~ số test tương ứng với số điểm có với ~T≤5000;~
• Có ~30\%~ số test khác tương ứng với số điểm có với ~Q≤500;~
• Có ~20\%~ số test còn lại tương ứng với số điểm không có giới hạn gì thêm~.~