Xét hai số nguyên dương ~u, v~, ta gọi thao tác ghép hai số ~u, v~ là thao tác viết số ~v~ sau số ~u~.

Ví dụ: Với ~u = 123, v = 456~, sau khi ta ghép hai số ~u, v~ với nhau, ta được số ~123456~.

Cho ~n~ số nguyên dương ~a_1, a_2, ..., a_n~.

Hãy cho biết: Có bao nhiêu cặp chỉ số ~(i, j) \ (1 \le i \lt j \le n)~ sao cho khi ta thực hiện thao tác ghép hai số ~a_i, a_j~, ta được một số mới chia hết cho ~3~?

Input

• Dòng đầu tiên chứa số nguyên dương ~n \ (n \ge 2);~
• Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n.~

Output

In ra kết quả là số cặp chỉ số ~(i, j)~ thoả mãn đề bài.

Scoring

• Subtask 1 [20%]: ~n \le 1000; \ a_i \le 10^9;~
• Subtask 2 [40%]: ~n \le 10^5; \ a_i \le 10^{18};~
• Subtask 3 [40%]: ~n \le 10^5; \ a_i \le 10^{100}.~

Examples

Input

7
123 4 5 7 10 3 2

Output

7

Giải thích: Các cặp chỉ số thoả mãn yêu cầu đề bài là: ~(1, 6), (2, 3), (2, 7), (3, 4), (3, 5), (4, 7), (5, 7).~

Cho dãy số nguyên ~a = (a_1, a_2, ..., a_n)~ bạn được thay số ~0~ trong ~a~ bởi một số nguyên bất kỳ khác sau đó chọn ra trong dãy ~a~ một số nhiều nhất các số (không cần đúng thứ tự) sao cho các số đã chọn tạo thành một dãy số nguyên liên tiếp.

Yêu cầu: Tìm cách có được dãy số nguyên liên tiếp dài nhất theo cách trên.

Ví dụ với ~a = (1, 0 ,3 ,8 ,5 ,9 ,0)~, ta có thể thay hai số ~0~ lần lượt bởi ~6~ và ~7~, khi đó có thể chọn trong ~a~ ra các số ~(5, 6, 7, 8, 9)~ để được dãy số nguyên liên tiếp dài nhất.

INPUT

Dòng 1 chứa số nguyên dương ~n \le 10^6~

Dòng 2 chứa ~n~ số nguyên ~a_1, a_2, ..., a_n~ cách nhau bởi dấu cách (giá trị ~i~: ~|a_i| \le 10^6~)

OUTPUT

Số nguyên duy nhất là độ dài dãy số nguyên liên tiếp thu được theo phương án của bạn.

SAMPLE INPUT

7
1 0 3 8 5 9 0

SAMPLE OUTPUT

5

Trong lớp học toán ngày hôm nay của Cirno, cô ra một bài toán cho các học sinh của mình:

Cho một số nguyên dương, hãy đếm số cách xóa bỏ một chữ số (số còn lại có thể có số 0 ở đầu) để số còn lại chia hết cho 3, nhưng không chia hết cho 9 (vì cô không thích số 9).

Input:

• Một số nguyên dương ~n \le 10^{100000}~.

Output

• Số cách xóa thỏa mãn.

Sample Test

Input:

396

Output:

2

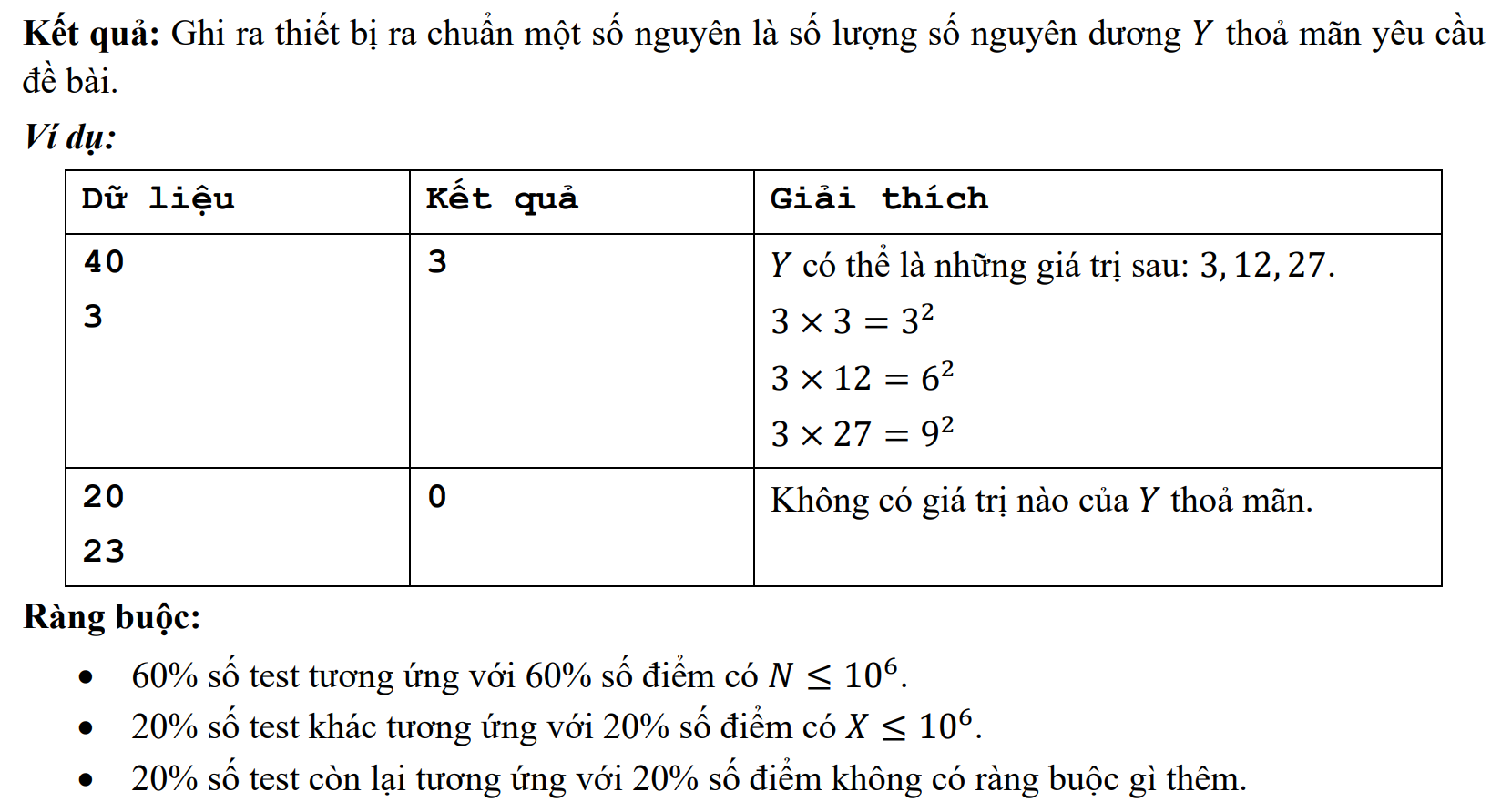
Giới hạn

• 60% số điểm: ~n \le 10^{1000}~
• 40% số điểm: Không có giới hạn gì thêm.

Cho mảng ~A~ có ~n~ phần tử nguyên dương, hãy chọn một tập con có ít nhất ba phần tử (không cần liên tiếp) của ~n~ phần tử sao cho tổng ba số bất kỳ trong tập con đã chọn không lớn hơn tổng các số còn lại trong mảng ~A~ và số lượng phần tử của tập con là lớn nhất.

INPUT

Dòng đầu tiên ghi số ~n~ (~4 \le n \le 10^4~)

Dòng tiếp theo ghi ~n~ số nguyên dương ~A_1, A_2, ..., A_n~ (~A_i \le 10^2~)

OUTPUT

Dòng duy nhất ghi số lượng phần tử được chọn

Nếu không thể chọn được tập con thoả mãn thì in ra ~0~

SAMPLE INPUT

8
6 9 4 3 7 2 5 1

SAMPLE OUTPUT

7

Giải thích: Các phần tử được chọn là ~6, 4, 3, 7, 2, 5, 1~

Cho một dãy số nguyên dương ~a~, đếm số lượng dãy con liên tiếp có tổng chia hết cho ~d~

Hai dãy con được gọi là khác nhau nếu ít nhất một trong hai điểm đầu hoặc điểm cuối hay dãy con đó trong dãy gốc là khác nhau.

Ví dụ:

• Với ~d = 4~, dãy (~2, 1, 2, 1, 4, 1~) có ~4~ dãy con thoả mãn là (~1, 2, 1~), (~1, 2, 1, 4~), (~4~), (~2, 1, 4, 1~)

• Với ~d = 2~, dãy (1, 1, 1, 1) có ~4~ dãy con thoả mãn

INPUT

Dòng đầu tiên là số ~t~ - số lượng test (~t \le 100~)

~t~ nhóm dòng tiếp theo, mỗi nhóm dòng tương ứng với một yêu cầu:

• Dòng đầu là hai số nguyên dương ~d~ và ~n~ (~d \le 10^6~, ~n \le 5 * 10^4~)

• Dòng thứ hai chứa ~n~ số nguyên dương biểu diễn dãy số

OUTPUT

~t~ dòng là kết quả của các test theo thứ tự

SAMPLE INPUT

1
2 4
1 1 1 1

SAMPLE OUTPUT

4

Giải thích: Các cặp (~i, j~) sau thoả mãn: (~1, 2~), (~2, 3~), (~3, 4~), (~1, 4~)

debugging /diːˈbʌɡɪŋ/ (v.): Being the detective in a crime movie where you are also the murderer.

MrTee đang có một dãy gồm ~N~ số nguyên dương ~a_1, a_2, \dots, a_N~ và cũng có một chiếc máy quét mới mua (ở Ý, rất đắt). Khi đặt chiếc máy quét vào vị trí thứ ~i~, chiếc máy sẽ hiện số lượng các số mà bằng với ~a_i~ trong dãy mà có khoảng cách tới ~i~ không quá ~K~, kể cả chính nó. Vì quá mệt mỏi vì học sinh quá báo trong kì thi vừa rồi, MrTee đã nhờ bạn giúp MrTee thử chiếc máy này xem ở mỗi vị trí ~i~ từ ~1~ đến ~N~, chiếc máy sẽ trả về giá trị bao nhiêu.

Nói cách khác, cho một dãy ~N~ số nguyên dương ~a_1, a_2, \dots, a_N~, với mỗi ~i~, bạn cần tìm số lượng số ~j~ thỏa mãn ~a_i = a_j~ và ~|i - j| \le K~ ~(1 \le i, j \le N)~.

Liệu bạn có phải pro player hay cũng báo thầy như học sinh của MrTee?

Input

• Dòng đầu tiên gồm hai số nguyên dương ~N, K~ ~(K \le N)~.
• Dòng thứ hai gồm ~N~ số nguyên dương ~a_1, a_2, \dots, a_N~ ~(1 \le a_i \le 10^5)~.

Output

• Gồm một dòng gồm ~N~ số nguyên, số thứ ~i~ là đáp án nếu ta đặt máy quét vào vị trí thứ ~i~.

Scoring

• Subtask 1 ~(60 \%)~: ~K \le N \le 2000~.
• Subtask 2 ~(40 \%)~: ~K \le N \le 10^5~.

Sample Input

6 2
1 1 2 2 2 1

Sample Output

2 2 3 3 3 1

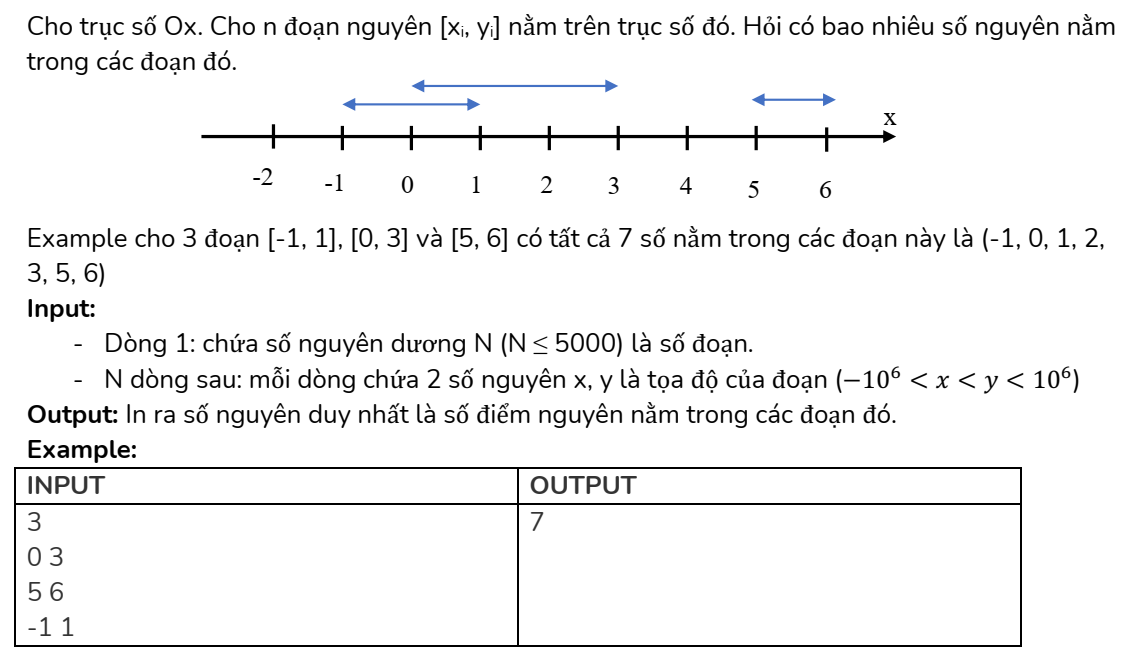
Trên trục số ~Ox~, cho ~𝑁~ đoạn thẳng, mỗi đoạn thẳng được xác định bởi hai điểm đầu và cuối là hai số nguyên. Một điểm ~𝑀~ được gọi là nằm trong đoạn thẳng ~𝐴𝐵~ nếu ~𝐴 ≤ 𝑀 ≤ 𝐵~.

Yêu cầu: Đếm xem có bao nhiêu điểm có toạ độ nguyên nằm trong đúng ~𝐾~ đoạn thẳng.

Dữ liệu nhập vào từ file văn bản DC.INP:

• Dòng đầu tiên gồm hai số nguyên ~𝑁~ và ~𝐾~ ~(1 ≤ 𝐾 ≤ 𝑁 ≤ 10^5);~
• ~𝑁~ dòng sau, mỗi dòng gồm hai số nguyên ~𝑎, 𝑏~ mô tả hai điểm đầu và cuối của đoạn thẳng ~(1 ≤ 𝑎 ≤ 𝑏 ≤ 10^{18})~.

Kết quả ghi ra file văn bản DC.OUT:

Một số nguyên duy nhất là số lượng điểm có toạ độ nguyên nằm trong đúng ~𝐾~ đoạn thẳng.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm của bài thoả mãn: ~𝑎, 𝑏 ≤ 10^3;~
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thoả mãn: ~𝐾 = 𝑁;~
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

3 2
1 5
2 8
3 7

Output

3

Giải thích: Toạ độ của ~3~ điểm nằm trong đúng ~2~ đoạn thẳng là: ~2, 6, 7~.

• Điểm có toạ độ ~2~ nằm trong ~2~ đoạn thẳng: đầu tiên và thứ hai.
• Điểm có toạ độ ~6, 7~ nằm trong ~2~ đoạn thẳng: thứ hai và thứ ba.

Input

3 1
1 5
2 8
3 7

Output

2   

Giải thích: Toạ độ của ~2~ điểm nằm trong đúng ~1~ đoạn thẳng là: ~1, 8~.

• Điểm có toạ độ ~1~ chỉ nằm trong đoạn thẳng đầu tiên.
• Điểm có toạ độ ~8~ chỉ nằm trong đoạn thẳng thứ ba.

Input

3 3
1 5
2 8
3 7

Output

3

Giải thích: Toạ độ của ~3~ điểm nằm trong cả ~3~ đoạn thẳng là: ~3,4,5~.

Cho hai đường thẳng ~d_1: y = y_1~ và ~d_2: y = y_2~. Cho ~n~ điểm phân biệt trên đường thẳng ~d_1~ (có hoành độ ~x_{11}~, ~x_{12}~, ..., ~x_{1n}~) và ~m~ điểm phân biệt trên đường thẳng ~d_2~ (có hoành độ ~x_{21}~, ~x_{22}~, ..., ~x_{2m}~). Hãy tìm khoảng cách Manhattan nhỏ nhất giữa hai điểm ~(A, B)~ với ~A \in d_1~ và ~B \in d_2~ và đếm số cặp điểm ~(A, B)~ phân biệt có khoảng cách Manhattan nhỏ nhất.

Input

• Dòng đầu tiên chứa hai số nguyên dương ~n~, ~m~ (~n, m \le 10^6~)
• Dòng thứ hai chứa hai số nguyên ~y_1~, ~y_2~ (~-10^9 < y_1, y_2 < 10^9~)
• Dòng thứ ba chứa ~n~ số nguyên phân biệt ~x_{11}~, ~x_{12}~, ..., ~x_{1n}~ (~-10^9 < x_{1i} < 10^9~)
• Dòng thứ tư chứa ~m~ số nguyên phân biệt ~x_{21}~, ~x_{22}~, ..., ~x_{2m}~ (~-10^9 < x_{2i} < 10^9~)

Output

• Một dòng duy nhất gồm hai số nguyên: khoảng cách Manhattan ngắn nhất và số cặp có khoảng cách như vậy.

Sample Test

Input

3 4
1 -2
3 0 6
5 -2 4 2

Output

4 3

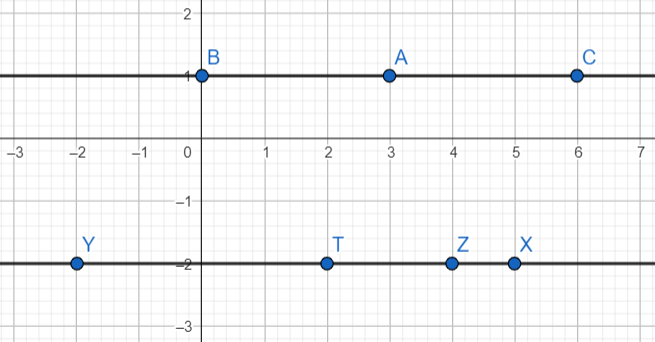
Giải thích

Có ~3~ cặp điểm ~(A, T)~, ~(A, Z)~, ~(C, X)~

Công ty đồ chơi của hoangduong nhập khẩu ~n~ con búp bê kachusa. Các con búp bê được đánh số từ ~1~ tới ~n~ trong đó con búp bê thứ ~i~ là một hộp rỗng có kích thước là một số nguyên ~a_i~. Người ta có thể lồng con búp bê thứ ~i~ vào trong con búp bê thứ ~j~ nếu con búp bê thứ ~j~ đang rỗng và ~a_i + k \le a_j~, với ~k~ là một số nguyên dương cho trước. Bằng cách lồng các con búp bê vào nhau theo cách như vậy, công ty của hoangduong chỉ cần tìm chỗ đặt những con búp bê ngoài cùng (những con búp bê không nằm trong bất kỳ con búp bê nào khác) vào kho.

Yêu cầu: Hãy giúp hoangduong lồng các con búp bê vào nhau sao cho tổng kích thước các con búp bê ngoài cùng là nhỏ nhất.

INPUT

Dòng 1 chứa hai số nguyên dương ~n \le 10^5~; ~k \le 10^9~ cách nhau một khoảng trắng.

Dòng 2 chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ (~a_i \le 10^9~), mỗi số cách nhau một khoảng trắng.

OUTPUT

Là một số nguyên duy nhất là tổng kích thước các con búp bê ngoài cùng theo phương án tìm được.

SAMPLE INPUT

8 2
8 4 2 1 1 3 5 9

SAMPLE OUTPUT

18

Trong lúc buồn chán hoangduong đã tìm một xâu ~S~ có độ dài ~n~ kí tự là các chữ cái tiếng Anh in thường và đảo ngược một số xâu con liên tiếp của xâu ~S~. Hãy viết chương trình tìm xâu ~S~ sau khi hoangduong thực hiện lần lượt ~m~ lần đảo xâu như trên.

INPUT

• Dòng đầu tiên gồm một xâu ~S~ có độ dài ~n~ mà hoangduong tìm được bạn đầu (~1 \le n \le 200000~)
• Dòng thứ hai gồm một số nguyên ~m~ (~1 \le m \le 100000~) là số lẫn mà hoangduong đảo một xâu con liên tiếp của xâu ~S~
• Dòng thứ ba gồm ~m~ số tự nhiên ~a_i~ (~1 \le a_i \le n / 2~), mỗi số mô tả lần đảo một xâu con liên tiếp từ kí tự thứ ~a_i~ đến kí tự thứ ~n - a_i + 1~ của Na. Các kí tự trong ~S~ được đánh số từ ~1~ đến ~n~.

OUTPUT

Gồm một dòng duy nhất chứ một xâu là xâu ~S~ sau khi hoangduong đã thực hiện lần lượt ~m~ lần đảo

SAMPLE INPUT 1

kcchinbayble
4
2 2 2 2

SAMPLE OUTPUT 1

kcchinbayble

SAMPLE INPUT 2

haideu
1
1

SAMPLE OUTPUT 2

uediah

Đằng sau một lập trình viên thành công là một cô bạn gái... không tồn tại 🗿

Nhân dịp sinh nhật, Tèo được thưởng một chiếc điện thoại Nakio. Một ngày nọ, mải chụp ảnh up story, cậu vô tình làm rơi chiếc điện thoại của mình làm cho bàn phím của nó hoạt động một cách rất ảo diệu. Khi nhấn vào một phím, chiếc điện thoại lại hiện ra các ký tự của phím khác. May mắn thay là không có hai phím nào hoạt động giống nhau nên Tèo vẫn có thể viết được tất cả các chữ cái. Sau một hồi tìm hiểu, cậu ấy đã tìm được cách hoạt động của các phím.

Đây là cách thức hoạt động của bàn phím điện thoại khi nó vẫn chưa bị hỏng. Bàn phím hoạt động gần tương tự với bộ gõ T9 trên những chiếc điện thoại cục gạch quen thuộc của nhiều thế hệ. Muốn gõ được chữ a, ta cần nhấn phím 2 một lần; muốn gõ được chữ b, ta cần nhấn phím 2 hai lần. Nếu muốn viết hai chữ cái nằm trên cùng một phím thì sau khi gõ chữ cái đầu tiên, ta cần nhấn phím # một lần rồi sau đó gõ chữ cái tiếp theo. Ví dụ, muốn viết xâu abc, ta cần nhấn theo thứ tự 2#22#222. Phím 0 hoạt động như dấu cách, 1 và * không hoạt động.

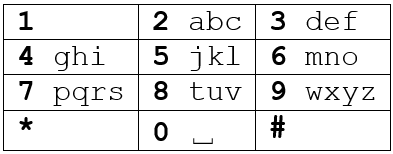
Tèo vừa chia tay với người yêu nên cậu ấy muốn up story suy suy thất tình lên mạng xã hội F bằng chiếc điện thoại của mình. Hãy chỉ ra thứ tự các phím cần nhấn để viết được dòng caption đó.

Input

• Dòng đầu tiên chứa ~9~ số nguyên phân biệt từ ~1~ đến ~9~ có ý nghĩa: Số thứ ~1~ là cách hoạt động của phím 1, số thứ ~2~ là cách hoạt động của phím 2, ..., số thứ ~9~ là cách hoạt động của phím 9 (nghĩa là nếu số thứ ~2~ là 3 thì lúc này phím 2 sẽ hoạt động như phím 3).
• Dòng thứ hai là một xâu gồm các chữ cái tiếng Anh viết thường (có thể có dấu cách) có độ dài không quá ~100~ là nội dung của story mà Tèo muốn up lên trang F. Dữ liệu đảm bảo sau ký tự cuối cùng của caption không có dấu cách.

Output

Một xâu mô phỏng thứ tự các phím cần nhấn để viết được dòng caption của Tèo.

Scoring

• Subtask 1 [50%]: Bàn phím của Tèo không bị hỏng. Nói cách khác, ở dòng đầu tiên, số thứ ~i~ có giá trị là ~i~ ~(1\le i\le 9)~.
• Subtask 2 [50%]: Không có ràng buộc gì thêm.

Ví dụ

Input

1 2 3 4 5 6 7 8 9
den do roi kia minh dung lai em nhe

Output

3#3366036660777666444055444206444664403886640555244403360664433

Input

4 6 2 5 1 7 9 3 8
nhin sang trai vi em khong phai cua anh

Output

2211#111220666632210966631110999111088204411222#221061131110333993032211

Cho một dãy gồm ~n~ số nguyên dương ~a_1, a_2, a_3, \ldots, a_n~ là hoán vị của các số nguyên từ ~1~ đến ~n~. Sử dụng các thao tác lần lượt đổi chỗ hai số ở vị trí ~i~ và ~j~ bất kỳ, hãy sắp xếp dãy ban đầu thành dãy tăng dần.

Input

• Dòng đầu tiên chứa số nguyên dương ~n~ (~n \leq 10^5~).
• Dòng tiếp theo chứa ~n~ số nguyên dương ~a_1, a_2, a_3, \ldots, a_n~ là hoán vị của các số nguyên từ ~1~ đến ~n~.

Output

• Dòng đầu tiên in ra số ~k~ (~0 \leq k \leq 2 \times 10^5~) - số lượng thao tác cần dùng.
• ~k~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~i~, ~j~ cách nhau một khoảng trắng (~1 \leq i, j \leq n~) thể hiện một thao tác đổi ~a_i~ và ~a_j~ cho nhau.

Có thể chứng minh được rằng luôn tồn tại cách sắp xếp thoả mãn không sử dụng quá ~2 \times 10^5~ thao tác.

Subtasks

• Subtask ~1~ (~10\%~): ~n = 3~.
• Subtask ~2~ (~20\%~): ~n \leq 100~.
• Subtask ~3~ (~30\%~): ~n \leq 10^4~.
• Subtask ~4~ (~40\%~): Không có ràng buộc gì thêm.

Sample Test

Input:

4
3 4 1 2

Output:

2
1 3
2 4

Một dãy số được gọi là ~''~đẹp~''~ nếu mỗi phần tử trong dãy đó đều có số lần xuất hiện không vượt quá ~2~. Ví dụ:

• ~[1, 5, 2, 4, 3], [6, 9, 9, 6], [100]~ là các dãy đẹp.
• ~[3, 3, 3, 4, 4], [7, 7, 8, 7]~ và ~[100, 100, 100]~ không phải là các dãy đẹp.

Cho dãy ~a~ có ~n~ phần tử, hãy đếm số cặp chỉ số ~(l, r)~ sao cho ~a_l, a_{l+1}, ..., a_r~ là dãy đẹp.

Input

• Dòng đầu tiên chứa số nguyên dương ~n;~
• Dòng tiếp theo chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n.~

Output

In ra kết quả là số cặp chỉ số ~(l, r)~ thoả mãn đề bài.

Scoring

• Subtask 1 [20%]: ~n \le 50; \ a_i \le 50;~
• Subtask 2 [15%]: ~n \le 500; \ a_i \le 500;~
• Subtask 3 [15%]: ~n \le 5000; \ a_i \le 5000;~
• Subtask 4 [50%]: ~n \le 5 \times 10^5; \ a_i \le 5 \times 10^5.~

Examples

Input

4
1 2 1 1

Output

9

Giải thích: Các cặp chỉ số ~(l, r)~ thoả mãn đề bài là: ~(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4).~

Input

6
4 5 4 5 4 5

Output

18