Một số nguyên dương ~A~ được gọi là hoàn hảo nếu ~2 \times A \leq K~, với ~K~ là tổng các ước dương của ~A~.

Ví dụ, ~12~ là số hoàn hảo vì ~2 * 12 \leq K~ với ~K = 1 + 2 + 3 + 4 + 6 + 12 = 28.~

Cho ~N~ số nguyên dương ~A_1, A_2, \ldots, A_n~, hãy đếm số lượng số hoàn hảo trong dãy đã cho.

Input

• Dòng đầu tiên chứa số nguyên dương ~N~. (~N \leq 10^4~)
• ~N~ dòng tiếp theo, dòng thứ ~i~ chứa số nguyên dương ~A_i~. (~A_i \leq 10^6~)

Output

• In ra số lượng số hoàn hảo trong dãy đã cho.

Sample Test

Input:

5
8
16
12
6
7

Output:

2

Cho một dãy gồm ~N~ số nguyên dương ~a_1, a_2, a_3, ..., a_N~. Biết rằng các số trong dãy đều xuất hiện hai lần, trừ một số. Hãy tìm số đó.

Input

• Dòng thứ nhất chứa số nguyên dương ~N~.
• Dòng thứ hai chứa ~N~ số nguyên dương ~a_1, a_2, a_3, ... a_N~. (~a_i \leq 10^6~)
• Các số đều xuất hiện hai lần trừ một số.

Output

• In ra số chỉ xuất hiện một lần trong dãy.

Subtasks

• Subtask 1 (~20\%~ số điểm): ~N = 3~.
• Subtask 2 (~30\%~ số điểm): ~N \leq 10^3~.
• Subtask 3 (~50\%~ số điểm): ~N \leq 10^6~.

Sample Test 1

Input

5
4 1 2 1 2

Output

4

TDZ mới có một bộ đồ chơi xếp hình bằng gỗ mới. Tuy nhiên TDZ rất nhanh đã chán với việc xếp hình, vì vậy TDZ sáng chế ra một trò với chiếc hộp đựng.

TDZ cẩn thận xếp các miếng xếp hình hình vuông vào hộp thành ~N~ chồng, mỗi chồng có ~A_i~ miếng. Sau đó TDZ đóng hộp, xoay hộp ~90~ độ sang phải, và xoay lại hộp ~90~ độ sang trái.

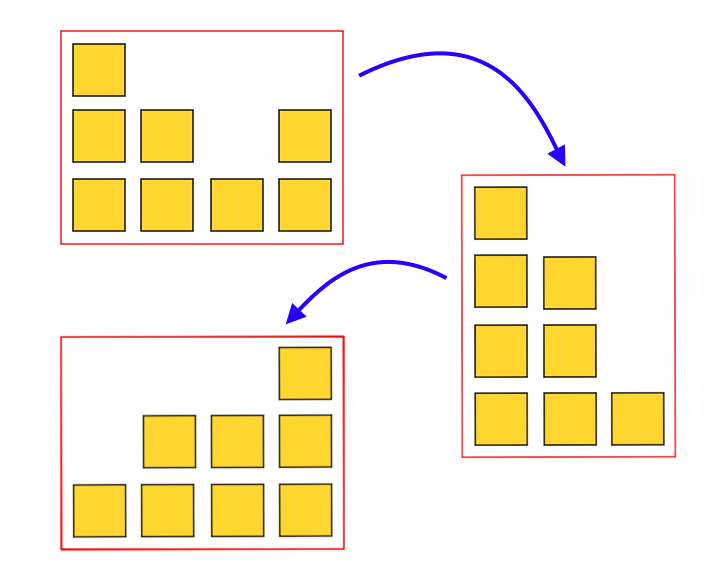
Hãy đưa ra chiều cao của các chồng sau khi TDZ xoay hộp như trên.

Input

• Dòng đầu tiên chứa số nguyên ~N~ (~N \leq 5000~).
• Dòng thứ hai chứa ~N~ số nguyên dương ~A_1, A_2, \ldots, A_N~ - chiều cao các chồng (~A_i \leq 10^9~).

Output

• In ra lần lượt chiều cao các chồng sau khi xoay hộp, mỗi số cách nhau một khoảng trắng.

Sample Test 1

Input:

4
3 2 1 2

Output:

1 2 2 3

Sample Test 2

Input:

3
1 2 5

Output:

1 2 5

Con phố ~X~ có ~n~ cái cột đèn được đánh số từ ~1~ đến ~n~. Tuy nhiên, trận bão tàn khốc vừa qua đã khiến ~t~ trong ~n~ cây đèn này bị đổ. Sắp tới, thành phố cần tổ chức một lễ hội lớn tại đây, và yêu cầu cần tổ chức tại vị trí có ít nhất ~k~ cái đèn còn nguyên vẹn liên tiếp. Vì thời gian gấp rút, bạn được thành phố yêu cầu tìm xem cần phải sửa chữa ít nhất bao nhiêu cây đèn để có thể tổ chức lễ hội.

Input

• Dòng đầu tiên gồm ba số nguyên dương ~n, k, t~ ~(1 \le t, k \le n \le 10^5)~.
• ~t~ dòng tiếp theo, mỗi dòng gồm một số nguyên dương là vị trí có cây đèn bị đổ.
  
  

Output

• In ra một số nguyên duy nhất là số cây đèn cần được sửa chữa.
  
  

Sample Test

Input:

10 6 5
2
10
1
5
9

Output:

1

Note: Sửa cây đèn tại vị trí ~5~ và chọn các cây ~3, 4, 5, 6, 7~ để tổ chức lễ hội.

Cho số ~n~. Hãy tìm số ~k \le n~ lớn nhất sao cho ~k~ là tích của 3 số nguyên tố liên tiếp.

Input

• Gồm số tự nhiên ~n \le 10^{18}~.

Output

• Gồm duy nhất một số tự nhiên ~k~. Nếu không có số thỏa mãn in ra -1.

Sample Test

Input:

31

Output

30

Điều kiện thoả mãn dãy ngoặc đúng được định nghĩa như sau:

• Dãy rỗng "" là một dãy ngoặc đúng.
• Nếu dãy ~A~ là một dãy ngoặc đúng thì ~(A)~ là một dãy ngoặc đúng.
• Nếu dãy ~A~ và dãy ~B~ là hai dãy ngoặc đúng thì ~A + B~ là một dãy ngoặc đúng.

Cho xâu ~s~ là một dãy ngoặc chỉ gồm 2 kí tự là ~(~ và ~)~, hãy kiểm tra xem xâu ~s~ có phải một dãy ngoặc đúng hay không.

Input

• Gồm một dòng chứa xâu ngoặc ~s~ ~(1 \le |s| \le 10^3)~.

Output

• In ra Yes nếu xâu ~s~ là dãy ngoặc đúng, ngược lại in ra No.

Ví dụ

Input 1:

(()())

Output 1:

Yes

Input 2:

(()))

Output 2:

No

Trên quốc lộ ~1A~ có ~N + 1~ trạm xăng từ đầu đến cuối con đường, đánh số từ ~0~ đến ~N~. Biết trạm xăng số ~i~ cách trạm xăng số ~i - 1~ một khoảng ~a_i~ km và trạm xăng số ~i~ bán ~1~ lít xăng với giá ~p_i~ đồng. Để đi được ~1~ km ta cần tiêu tốn ~1~ lít xăng.

TDZ đang bắt đầu đi trên quốc lộ ~1A~ thì hết xăng nên phải dừng tại trạm xăng số ~0~. Tính số tiền mua xăng nhỏ nhất mà TDZ phải mua để đến được trạm xăng số ~N~.

Input

• Dòng đầu tiên chứa số nguyên dương ~N~ (~N \leq 10^5~).
• Dòng thứ hai chứa ~N~ số nguyên dương ~a_1, a_2, \ldots, a_N~ (~a_i \leq 10^9~).
• Dòng thứ ba chứa ~N~ số nguyên dương ~p_0, p_1, \ldots, p_{N - 1}~ (~p_i \leq 10^9~).

Output

• In ra tổng số tiền nhỏ nhất dùng mua xăng để TDZ đến được trạm xăng số ~N~.

Sample Test

Input:

3
1 2 4
3 1 2

Output:

9

Note:

• TDZ mua ~1~ lít xăng ở trạm xăng thứ ~0~ (giá ~3~ đồng) để đi đến trạm xăng số ~1~.
• TDZ mua ~6~ lít xăng ở trạm xăng thứ ~1~ (giá ~6~ đồng) để đi đến trạm xăng cuối cùng.

Sau thành công từ quán cà phê nổi tiếng của mình, TDZ quyết định tự thưởng cho bản thân.

Ở cửa hàng có trưng bày ~n~ món hàng, món thứ ~i~ có giá ~v_i~. Với tổng số tiền ~x~ trong tay, TDZ muốn mua 2 món quà khác nhau có tổng giá trị lớn nhất và tất nhiên không vượt quá khả năng chi trả của mình. TDZ đang loay hoay không biết phải chọn món nào, bạn hãy giúp TDZ nhé.

Input

• Dòng đầu tiên chứa số nguyên dương ~n~ và ~x~ lần lượt là số món hàng và số tiền TDZ sở hữu (~2 \leq n \leq 10^5, x \leq 10^9~).
• Dòng tiếp theo chứa ~n~ số nguyên dương ~v_1, v_2, v_3, \ldots, v_n~ tương ứng với giá tiền từng món hàng (~v_i \leq 10^9~).

Output

In ra số tiền cần trả, hoặc 0 nếu TDZ không thể chọn được ~2~ món thoả mãn.

Subtasks

• Subtask 1 (~50\%~): ~n \leq 10^3~.
• Subtask 2 (~50\%~): Không có điều kiện gì thêm.

Sample Test

Input:

6 18
5 3 10 2 4 9

Output:

15

Note: Ở ví dụ trên TDZ sẽ chọn món thứ nhất và thứ ba. Tổng số tiền cần chi sẽ là ~5 + 10 = 15~.

Ở đất nước Omega người ta chỉ tiêu tiền xu. Có ~N~ loại tiền xu, loại thứ ~i~ có mệnh giá là ~A_i~ đồng. Một người khách du lịch đến Omega du lịch với số tiền ~M~ đồng. Ông ta muốn đổi số tiền đó ra tiền xu Omega để tiện tiêu dùng.

Bạn hãy giúp ông ta tìm ~1~ cách đổi tiền để số đồng tiền đổi được là ít nhất (cho túi tiền đỡ nặng khi đi đây đi đó).

Input

• Dòng thứ nhất gồm hai số nguyên dương ~N~ và ~M~ (~N \leq 100, M \leq 10^3~).
• Dòng thứ hai gồm ~N~ số nguyên dương ~A_1, A_2, \ldots, A_N~ khác nhau (~A_i \leq 10^3, A_1 = 1~).

Output

• In ra số lượng đồng tiền ít nhất để đổi ~M~ đồng thành xu Omega.

Sample Test

Input:

3 8
1 4 5

Output:

2

Cho một dãy ~a~ gồm ~n~ phần tử. Ban đầu tất cả phần tử đều có giá trị bằng ~0~. Có ~m~ thao tác, thao tác thứ ~i~ gồm ba số nguyên ~L,R,X~ có nghĩa là tăng các phần tử từ vị trí thứ ~L~ tới vị trí thứ ~R~ lên ~X~ đơn vị.

Hãy tìm cách bỏ đi một thao tác để sau khi thực hiện hết ~M-1~ thao tác còn lại thì giá trị lớn nhất của dãy số là nhỏ nhất.

Input

• Dòng thứ nhất chứa ~2~ số nguyên dương ~n,m~.
• ~m~ dòng sau, mỗi dòng gồm ba số nguyên dương ~L,R,X~.
  
  

Output

• In ra giá trị lớn nhất của dãy số sau khi bỏ đúng một thao tác thỏa mãn yêu cầu đề bài.
  
  

Constraints

• ~1 \le n,m \le 10^5~.
• ~|x| \le 10^9~.
  
  

Subtasks

• ~25\%~ số test: ~N \le 10^2, M \le 10^2~.
• ~25\%~ số test: ~N \le 10^5, M \le 10^2~.
• ~25\%~ số test: ~N \le 10^2, M \le 10^5~.
• ~25\%~ số test: ~N \le 10^5, M \le 10^5~.
  
  

Sample Test 1

Input:

5 2
1 3 3
2 5 2

Output:

2

Sample Test 2

Input:

5 3
1 3 3
2 5 2 
5 5 8

Output:

5

Cho một cây có ~n~ đỉnh đánh số từ ~1~ đến ~n~ và đỉnh ~1~ là gốc. Mỗi đỉnh trên đều được tô màu, đỉnh thứ ~i~ được tô bởi màu ~a_i~.

Một tập hợp các đỉnh trên được gọi là đẹp nếu có hơn một nửa số đỉnh trong tập được tô bởi cùng một màu.

Có ~q~ truy vấn, mỗi truy vấn thuộc một trong các dạng sau:

• Truy vấn dạng: ~1~ ~u~, truy vấn này kiểm tra xem tập đỉnh gồm các đỉnh nằm trong cây con gốc ~u~ có phải là một tập đẹp hay không;
• Truy vấn dạng: ~2~ ~u~, truy vấn này kiểm tra xem tập đỉnh gồm các đỉnh nằm ngoài cây con gốc ~u~ có phải là một tập đẹp hay không;
• Truy vấn dạng: ~3~ ~u~ ~v~, truy vấn này kiểm tra xem tập đỉnh gồm các đỉnh nằm trên đường đi đơn từ ~u~ tới ~v~ (tính cả ~u~ và ~v~) có phải là một tập đẹp hay không.
  
  

Input

• Dòng đầu tiên chứa số nguyên dương ~n, q~ là số đỉnh của cây và số lượng truy vấn.
• Dòng thứ hai chứa ~n~ số, số thứ ~i~ là ~a_i~ mô tả màu sắc của đỉnh ~i~. ~(1 \le a_i \le n)~
• ~n - 1~ dòng tiếp theo, mối dòng chứa hai số nguyên dương ~u, v~ ~(1 \le u, v \le n)~ mô tả cạnh nối hai đỉnh ~u~ và ~v~.
• Tiếp theo gồm có ~q~ dòng mô tả các truy vấn. Các truy vấn thuộc ~1~ trong ~3~ dạng ~1~ ~u~, ~2~ ~u~ hoặc ~3~ ~u~ ~v~.
  
  

Output

• Với mỗi truy vấn, in ra kết quả lần lượt trên các dòng khác nhau.
  
  

Constraints

• ~1 \le n,q \le 50000~
  
  

Subtasks

• Subtask ~1~ ~(20\%)~: ~1 ≤ n, q ≤ 2 000~.
• Subtask ~2~ ~(20\%)~: ~1 ≤ n, q ≤ 50 000~ và mỗi đỉnh có tối đa ~2~ cạnh nối trực tiếp.
• Subtask ~3~ ~(20\%)~: ~1 ≤ n, q ≤ 50 000~ và ~1 ≤ ai ≤ 2~
• Subtask ~4~ ~(20\%)~: ~1 ≤ n, q ≤ 50 000~ và không có truy vấn loại ~3~.
• Subtask ~5~ ~(20\%)~: không có ràng buộc nào thêm.
  
  

Sample Test

Input:

8 5
2 3 3 1 2 1 3 1
1 2
1 3
2 4
2 5
3 7
5 6
6 8
1 2
3 4 6
2 6
2 5
3 1 5

Output:

1
-1
-1
3
2

Giải thích:

Dưới đây là hình vẽ của ví dụ thứ nhất với màu ~1~ được tô màu xám, màu ~2~ được tô màu đỏ và màu ~3~ được tô màu xanh.

• Truy vấn ~1~: xét các đỉnh trong cây con gốc ~2~ là ~{2, 4, 5, 6, 8}~, màu ~1~ xuất hiện ~3~ lần.
• Truy vấn ~2~: xét các đỉnh trên đường đi từ ~4~ đến ~6~ là ~{2, 4, 5, 6}~, không có màu nào xuất hiện quá ~2~ lần.
• Truy vấn ~3~: xét các đỉnh nằm ngoài cây con gốc ~6~ là ~{11, 2, 3, 4, 5, 7}~, không có màu nào xuất hiện quá ~13~ lần.
• Truy vấn ~4~: xét các đỉnh nằm ngoài cây con gốc ~5~ là ~{1, 2, 3, 4, 7}~, màu ~3~ xuất hiện ~3~ lần.
• Truy vấn ~5~: xét các đỉnh nằm trên đường đi từ ~1~ đến ~5~ là ~{1, 2, 5}~, màu ~2~ xuất hiện ~2~ lần.