Cho bốn số thực ~𝐴, 𝐵, 𝐶, 𝐷~. Hỏi tích của bốn số đó là số dương, số âm hay số ~0~.

Dữ liệu nhập vào từ file TBS.INP:

Gồm bốn dòng, mỗi dòng gồm một số thực lần lượt là bốn số ~𝐴, 𝐵, 𝐶, 𝐷~ ~(−10^{18} ≤ 𝐴, 𝐵, 𝐶, 𝐷 ≤ 10^{18})~.

Kết quả ghi ra file TBS.OUT:

Một số nguyên duy nhất là:

• ~1~ nếu tích bốn số là số dương~;~
• ~-1~ nếu tích bốn số là số âm~;~
• ~0~ nếu tích bốn số là số ~0.~

Ví dụ

Input

20.21
-1.2
-2.3
1.0

Output

1

Input

5.0
-8.9
0.0
123.456

Output

0

Cho một robot được lập trình di chuyển trên một hàng ngang gồm các ô vuông. Mỗi ô được đặt tên bằng các kí tự theo thứ tự từ ~'𝐴'~ đến ~'𝑍'~ và được lặp lại vô hạn. Ban đầu robot xuất phát ở ô thứ ~1~ có tên là ~'𝐴'~ và nhảy đến các ô tiếp theo quy luật: lần ~1~ nhảy ~1~ ô, lần ~2~ nhảy ~2~ ô, lần ~3~ nhảy ~3~ ô, ~…~, lần ~𝑁~ nhảy ~𝑁~ ô. Vậy sau ~𝑁~ lần nhảy thì robot đang ở ô nào?

Dữ liệu nhập vào từ file văn bản DKT.INP:

Gồm một số nguyên dương ~N~ là số lần nhảy của robot ~(N \le 10^9)~.

Kết quả ghi ra file văn bản DKT.OUT:

Một kí tự duy nhất là tên của ô sau ~N~ lần robot nhảy.

Ràng buộc

• Có ~60\%~ số test ứng với ~60\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10^3;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10^6;~
• ~20\%~ số test còn lại ứng với 20% số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

1

Output

B

Giải thích: Sau ~1~ lần nhảy, robot ở ô thứ ~2~, có tên là kí tự ~B~.

Input

4

Output

K

Giải thích: Sau ~4~ lần nhảy, robot ở ô thứ ~11~, có tên là kí tự ~K~.

Input

7

Output

C

Giải thích: Sau ~7~ lần nhảy, robot ở ô thứ ~29~, có tên là kí tự ~C~.

Trên trục số ~Ox~, cho ~𝑁~ đoạn thẳng, mỗi đoạn thẳng được xác định bởi hai điểm đầu và cuối là hai số nguyên. Một điểm ~𝑀~ được gọi là nằm trong đoạn thẳng ~𝐴𝐵~ nếu ~𝐴 ≤ 𝑀 ≤ 𝐵~.

Yêu cầu: Đếm xem có bao nhiêu điểm có toạ độ nguyên nằm trong đúng ~𝐾~ đoạn thẳng.

Dữ liệu nhập vào từ file văn bản DC.INP:

• Dòng đầu tiên gồm hai số nguyên ~𝑁~ và ~𝐾~ ~(1 ≤ 𝐾 ≤ 𝑁 ≤ 10^5);~
• ~𝑁~ dòng sau, mỗi dòng gồm hai số nguyên ~𝑎, 𝑏~ mô tả hai điểm đầu và cuối của đoạn thẳng ~(1 ≤ 𝑎 ≤ 𝑏 ≤ 10^{18})~.

Kết quả ghi ra file văn bản DC.OUT:

Một số nguyên duy nhất là số lượng điểm có toạ độ nguyên nằm trong đúng ~𝐾~ đoạn thẳng.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm của bài thoả mãn: ~𝑎, 𝑏 ≤ 10^3;~
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thoả mãn: ~𝐾 = 𝑁;~
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

3 2
1 5
2 8
3 7

Output

3

Giải thích: Toạ độ của ~3~ điểm nằm trong đúng ~2~ đoạn thẳng là: ~2, 6, 7~.

• Điểm có toạ độ ~2~ nằm trong ~2~ đoạn thẳng: đầu tiên và thứ hai.
• Điểm có toạ độ ~6, 7~ nằm trong ~2~ đoạn thẳng: thứ hai và thứ ba.

Input

3 1
1 5
2 8
3 7

Output

2   

Giải thích: Toạ độ của ~2~ điểm nằm trong đúng ~1~ đoạn thẳng là: ~1, 8~.

• Điểm có toạ độ ~1~ chỉ nằm trong đoạn thẳng đầu tiên.
• Điểm có toạ độ ~8~ chỉ nằm trong đoạn thẳng thứ ba.

Input

3 3
1 5
2 8
3 7

Output

3

Giải thích: Toạ độ của ~3~ điểm nằm trong cả ~3~ đoạn thẳng là: ~3,4,5~.

Trong một đất nước có ~𝑁~ thành phố được đánh số từ ~1~ đến ~𝑁~, các thành phố được nối với nhau bởi ~𝑁 − 1~ con đường hai chiều, đảm bảo hai thành phố bất kì có thể đi được đến nhau. Có ~𝑀~ thành phố đang có dịch bệnh. Người ta muốn chọn thành phố để xây dựng bệnh viện dã chiến sao cho: chỉ số an toàn từ thành phố đó đến thành phố đang có dịch bệnh bất kì đều không lớn hơn ~𝐾~ ~(𝐾~ là một số cho trước và chỉ số an toàn giữa hai thành phố ~X~ và ~𝑌~ được tính bằng tổng số con đường trên đường đi từ ~𝑋~ đến ~𝑌)~.

Yêu cầu: Em hãy lập trình để tính xem có thể xây dựng bệnh viện dã chiến ở bao nhiêu thành phố?

Dữ liệu nhập vào từ file văn bản BV.INP:

• Dòng đầu tiên gồm ba số nguyên dương ~𝑁, 𝑀, 𝐾~ ~(1 ≤ 𝐾 ≤ 𝑀 ≤ 𝑁 ≤ 10^5)~ mô tả số lượng thành phố, số lượng thành phố đang có dịch bệnh và số ~K;~
• ~𝑁 − 1~ dòng sau gồm hai số nguyên ~𝑢~ và ~𝑣~ mô tả có con đường nối hai thành phố thứ ~𝑢~ và thứ ~𝑣~ ~(1 ≤ 𝑢, 𝑣 ≤ 𝑁);~
• Dòng tiếp theo gồm ~𝑀~ số nguyên ~𝑥~ mô tả những thành phố đang có dịch bệnh ~(1 ≤ 𝑥 ≤ 𝑁)~.

Kết quả ghi ra file văn bản BV.OUT:

Gồm một số nguyên duy nhất là số thành phố có thể thoả mãn để xây dựng bệnh viện dã chiến (thành phố đang có dịch bệnh cũng có thể xây dựng bệnh viện dã chiến).

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 500;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10^4;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: mỗi thành phố chỉ có đường đi trực tiếp đến tối đa hai thành phố khác~;~
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

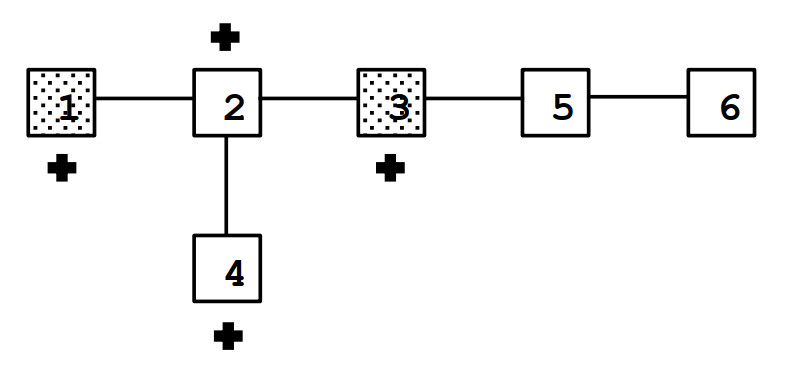
Input

6 2 2
1 2
3 2
3 5
4 2
5 6
1 3

Output

4

Giải thích: Có ~4~ thành phố có thể xây dựng bệnh viện dã chiến: ~1, 2, 3, 4~.

Input

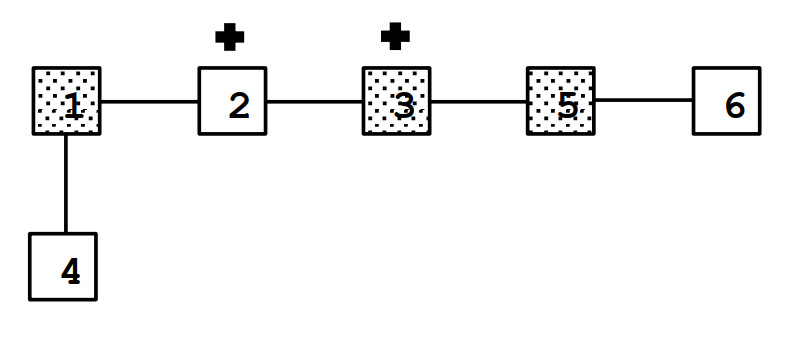
6 3 2
1 2
3 2
3 5
4 1
5 6
1 3 5

Output

2

Giải thích: Có ~2~ thành phố có thể xây dựng bệnh viện dã chiến: ~2, 3~. Thành phố ~4~ không xây dựng được bệnh viện dã chiến vì chỉ số an toàn từ thành phố ~4~ đến thành phố đang dịch bệnh ~5~ là ~4~.

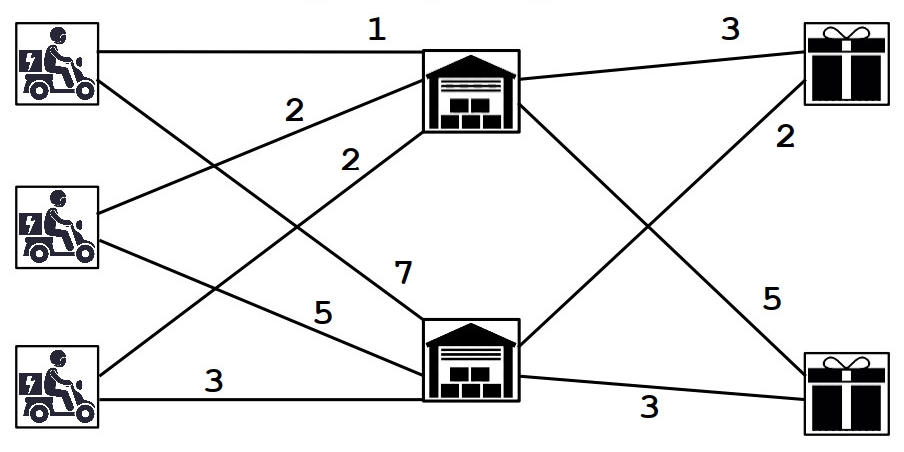
Cuối ngày làm việc của một công ty giao hàng, nhân viên tranh thủ giao đơn hàng cuối trước khi trở về nhà. Công ty có ~𝑁~ nhân viên giao hàng và ~𝑇~ yêu cầu chở hàng, mỗi nhân viên giao hàng thực hiện không quá một yêu cầu chở hàng. Có hai kho hàng, nhân viên giao hàng cần đến một trong hai kho này lấy hàng rồi di chuyển đến địa điểm cần giao. Cho biết khoảng cách từ ~𝑁~ nhân viên đến hai kho hàng và khoảng cách từ hai kho hàng đến ~𝑇~ địa điểm nhận hàng. Tìm tổng khoảng cách nhỏ nhất để thực hiện được toàn bộ ~𝑇~ yêu cầu chở hàng.

Yêu cầu: Em hãy tìm cách sắp xếp các nhân viên giao hàng sao cho tổng khoảng cách nhân viên phải di chuyển là nhỏ nhất để thực hiện được toàn bộ ~𝑇~ yêu cầu chở hàng.

Dữ liệu nhập vào từ file văn bản GH.INP:

• Dòng đầu tiên gồm hai số nguyên dương ~𝑁~ và ~𝑇~ ~(1 ≤ 𝑇 ≤ 𝑁 ≤ 10^5);~
• Dòng thứ hai gồm ~𝑁~ số nguyên ~𝑎1_𝑖~ là khoảng cách của nhân viên thứ ~𝑖~ đến kho ~1~ ~(1 ≤ 𝑖 ≤ 𝑁, \ 0 ≤ 𝑎1_𝑖 ≤ 10^9);~
• Dòng thứ ba gồm ~𝑁~ số nguyên ~𝑎2_𝑖~ là khoảng cách của nhân viên thứ ~𝑖~ đến kho ~2~ ~(1 ≤ 𝑖 ≤ 𝑁, \ 0 ≤ 𝑎2_𝑖 ≤ 10^9);~
• Dòng thứ bốn gồm ~𝑇~ số nguyên ~𝑏1_j~ là khoảng cách từ kho ~1~ đến địa điểm nhận hàng thứ ~𝑗~ ~(1 ≤ 𝑗≤ 𝑇, \ 0 ≤ 𝑏1_𝑖 ≤ 10^9);~
• Dòng thứ năm gồm ~𝑇~ số nguyên ~𝑏2_j~ là khoảng cách từ kho ~2~ đến địa điểm nhận hàng thứ ~𝑗~ ~(1 ≤ 𝑗 ≤ 𝑇, \ 0 ≤ 𝑏2_𝑖 ≤ 10^9).~

Kết quả ghi ra file văn bản GH.OUT:

Gồm một số nguyên duy nhất là tổng khoảng cách nhỏ nhất để thực hiện được toàn bộ ~𝑇~ yêu cầu chở hàng.

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm của bài thoả mãn: khoảng cách từ nhân viên giao hàng đến các kho bằng nhau và khoảng cách từ các kho đến địa điểm giao hàng bằng nhau, tức là: ~𝑎1_1 =𝑎2_1, \ 𝑎1_2 = 𝑎2_2, … , \ 𝑎1_𝑁 = 𝑎2_𝑁; \ 𝑏1_1 = 𝑏2_1, \ 𝑏1_2 = 𝑏2_2, … , \ 𝑏1_𝑇 = 𝑏2_𝑇;~
• ~10\%~ số test khác ứng với ~10\%~ số điểm của bài thoả mãn: khoảng cách từ nhân viên giao hàng đến các kho bằng nhau, tức là: ~𝑎1_1 = 𝑎2_1, \ 𝑎1_2 = 𝑎2_2, … , 𝑎1_𝑁 = 𝑎2_𝑁;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑇 ≤ 2;~
• ~10\%~ số test khác ứng với ~10\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10;~
• ~10\%~ số test khác ứng với ~10\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 100;~
• ~10\%~ số test khác ứng với ~10\%~ số điểm của bài thoả mãn: ~𝑇 ≤ 100;~
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

3 2
1 2 2
7 5 3
3 5
2 3

Output

10

Giải thích: Cách sắp xếp giao hàng:

• Nhân viên giao hàng thứ ~1~, đến kho ~1~, giao hàng đến địa điểm thứ ~1~. Khoảng cách là ~1 + 3 = 4~.
• Nhân viên giao hàng thứ ~3~, đến kho ~2~, giao hàng đến địa điểm thứ ~2~. Khoảng cách là ~3 + 3 = 6~.

Vậy tổng khoảng cách là ~10~.