Trong phòng thí nghiệm chỉ có đúng ba loại cốc có dung tích là ~5 \ (ml)~, ~3 \ (ml)~ và ~2 \ (ml)~. Hỏi cần ít nhất bao nhiêu lần đong nước để lấy được đúng ~N \ (ml)~.

Dữ liệu vào từ file văn bản DONGNUOC.INP:

Một số nguyên dương duy nhất ~N~ ~(2 \le N \le 10^{18})~ là số nước cần đong.

Kết quả ghi ra file văn bản DONGNUOC.OUT:

Một số nguyên dương duy nhất là số lượng lần đong ít nhất thoả mãn yêu cầu đề bài.

Ví dụ

Input

12

Output

3

Giải thích

Đong hai lần bằng cốc ~5 \ (ml)~ và một lần bằng cốc ~2 \ (ml)~.

Input

6

Output

2

Giải thích

Đong hai lần bằng cốc ~3 \ (ml)~.

Cho một dãy số gồm ~N~ số nguyên dương ~a_1, a_2, ..., a_N~ có giá trị không vượt quá ~10^6~. Tìm dãy con liên tiếp ngắn nhất có chứa ít nhất hai số nguyên tố.

Dữ liệu vào từ file văn bản DAYCON.INP:

• Dòng đầu tiên gồm một số nguyên dương ~N \ (N \le 10^6)~ là số lượng phần tử của dãy số;
• Dòng thứ hai gồm ~N~ số nguyên dương ~a_1, a_2, ..., a_N~ lần lượt mô tả các phần tử của dãy số.

Kết quả ghi ra file văn bản DAYCON.OUT:

Một số nguyên duy nhất là số lượng phần tử của dãy con thoả mãn đề bài. Trường hợp không tồn tại dãy con thoả mãn, in ra ~-1~.

Ví dụ

Input

10
3 4 8 4 5 6 1 7 4 6

Output

4

Giải thích

Chọn dãy con từ vị trí thứ ~5~ đến vị trí thứ ~8~: ~5, 6, 1, 7~.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm của bài thoả mãn: ~N \le 10^3; \ a_i \le 10^3~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thoả mãn: ~N \le 10^6; \ a_i \le 10^3~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Bản đồ thành phố X có dạng lưới ô vuông ~M~ hàng ~N~ cột, các hàng được đánh số từ ~1~ tới ~M~, các cột được đánh số từ ~1~ tới ~N~. Mỗi ô vuông trên bản đồ có thể là khu đất trống hoặc một khu dân cư hoặc một siêu thị.

Mỗi siêu thị chỉ có thể phục vụ các khu dân cư có khoảng cách so với nó không quá ~D~, nghĩa là nếu siêu thị nằm ở ô ~(x, y)~ thì nó có thể phục vụ được tất cả các khu dân cư nằm trong hình vuông có ô trái trên là ~(x - D, y - D)~, ô phải dưới là ~(x + D, y + D)~ (như Hình 1).

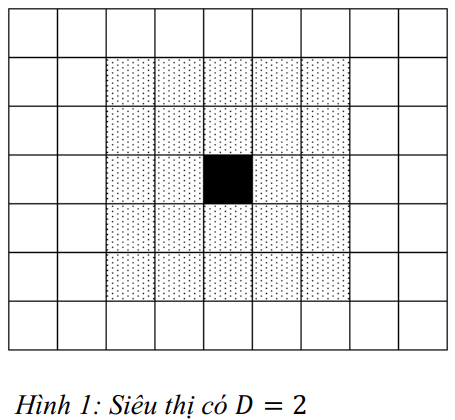
Một khu dân cư gọi là "chất lượng cao" nếu được ít nhất ~K~ siêu thị có thể phục vụ nó. Cho biết bản đồ của thành phố X, hãy đếm số lượng khu dân cư "chất lượng cao".

Dữ liệu vào từ file văn bản KHUDANCU.INP:

• Dòng đầu chứa bốn số nguyên ~M, N, D~ và ~K~ ~(1\le D \le \max(M, N); \ 1\le K\le M \times N)~;
• ~M~ dòng tiếp theo, mỗi dòng gồm ~N~ ký tự, mỗi ký tự biểu diễn một ô vuông bản đồ. Mỗi ký tự sẽ thuộc một trong ba loại sau:
  • . biểu diễn một khu đất trống;
  • P biểu diễn một khu dân cư;
  • M biểu diễn một siêu thị;

Dữ liệu đảm bảo tồn tại ít nhất một khu dân cư và ít nhất một siêu thị.

Kết quả ghi ra file văn bản KHUDANCU.OUT:

Ghi ra một số duy nhất là số khu dân cư "chất lượng cao".

Ví dụ

Input

5 5 1 2
P....
....P
..PM.
.M...
.....

Output

1

Giải thích

Bản đồ minh hoạ thành phố ~X~ như Hình 2.

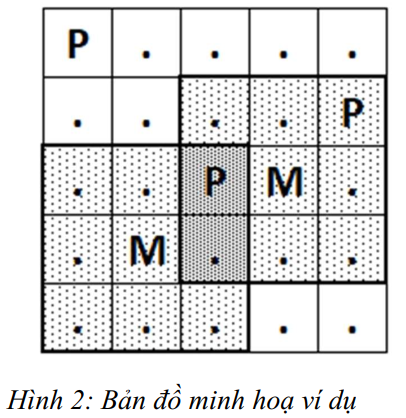
Khu dân cư ở ô ~(1, 1)~ không được siêu thị nào phục vụ;

Khu dân cư ở ô ~(2, 5)~ được một siêu thị có thể phục vụ;

Khu dân cư ở ô ~(3, 3)~ được hai siêu thị có thể phục vụ;

Vậy có một khu dân cư "chất lượng cao".

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thoả mãn: ~M = 1; \ N, D \le 10^3~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~M = 1; \ N \le 10^5~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~2 \le M, N \le 1000;~ số khu dân cư, số siêu thị không vượt quá ~1000~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài thoả mãn: ~2 \le M, N \le 1000~.

Một công ty gồm ~N~ người được đánh số từ ~1~ tới ~N~. Tổng giám đốc của công ty được đánh số là ~1~, mỗi người từ ~2~ tới ~N~ có đúng một cấp trên trực tiếp của mình.

Nếu ~i~ là cấp trên trực tiếp của ~j~, ta gọi ~i~ là quản lý của ~j~. Nếu ~i~ là quản lý của ~j~ thì ~i~ cũng là quản lý của những người mà ~j~ quản lý. Không có trường hợp ~i~ là quản lý của ~j~ đồng thời ~j~ là quản lý của ~i~.

Công ty có chế độ lương thưởng rất đặc biệt, người thứ ~i~ có lương là ~a_i~, người cấp dưới có thể có lương cao hơn người quản lý.

Công ty muốn tổ chức một sự kiện cho toàn bộ công ty. Nhưng nếu hai người ~u~ và ~v~ tham gia, trong đó ~u~ là quản lý của ~v~ mà lương của ~u~ không cao hơn lương của ~v~ ~(a_u \le a_v)~ thì sẽ gây ra bất hoà. Công ty muốn chọn ra được nhiều người nhất tham gia sự kiện mà không có sự bất hoà nào.

Phòng tổ chức sự kiện đã lên ~Q~ giả định như sau: Xét người ~u \ (1 \le u \le N)~, chọn ra một số người mà ~u~ là quản lý (có thể chọn hoặc không chọn ~u~) để tham gia sự kiện sao cho:

• Tổng số người được chọn là lớn nhất;
• Không có sự bất hoà nào giữa những người được chọn.

Yêu cầu: Với mỗi giả định, in ra số người nhiều nhất có thể chọn để tham gia sự kiện.

Dữ liệu vào từ file văn bản CONGTY.INP:

• Dòng đầu tiên chứa hai số nguyên dương ~N~ và ~Q~ ~(1 \le N, Q \le 2 \times 10^5)~;
• Dòng thứ hai gồm ~N~ số nguyên dương, số thứ ~i~ là ~a_i~ mô tả mức lương của người thứ ~i~ ~(1 \le a_i \le 10^9)~;
• Dòng thứ ba gồm ~N - 1~ số nguyên dương, số thứ ~i~ là ~p_i~ mô tả ~p_i~ là cấp trên trực tiếp của ~i+1~ ~(1 \le p_i \le N)~;
• ~Q~ dòng sau, dòng thứ ~i~ gồm một số nguyên dương ~u_i \ (1 \le u_i \le N)~, mô tả giả định thứ ~i~.

Kết quả ghi ra file văn bản CONGTY.OUT:

Với mỗi giả định, in ra kết quả tương ứng.

Ví dụ

Input

6 3
8 4 2 7 1 3
1 1 3 2 3
1
3
4

Output

5
2
1

Giải thích

Hình vẽ minh hoạ như Hình 3.

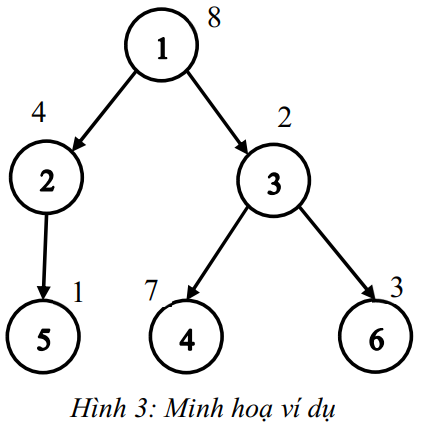
• Với giả định thứ nhất, chọn các nhân viên: ~1, 2, 5, 4, 6~;
• Với giả định thứ hai, chọn các nhân viên: ~4, 6~;
• Với giả định thứ ba, chọn nhân viên: ~4~.

Input

6 2
7 5 6 4 3 1
1 1 3 3 5
3
1

Output

4
6

Giải thích

• Với giả định thứ nhất, chọn các nhân viên: ~3, 4, 5, 6~;
• Với giả định thứ hai, chọn các nhân viên: ~1, 2, 3, 4, 5, 6~.

Ràng buộc

• Có ~15\%~ số test ứng với ~15\%~ số điểm của bài thoả mãn: ~N \le 15; \ Q = 1~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: nếu ~u~ là quản lý của ~v~ thì ~a_u > a_v~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm của bài thoả mãn: ~i~ là cấp trên trực tiếp của ~i+1~ ~(1 \le i \le N)~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm của bài thoả mãn: ~N \le 1000; \ a_i \le 100~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~N \le 10^5; \ a_i \le 100~;
• ~15\%~ số test còn lại ứng với ~15\%~ số điểm của bài không có ràng buộc gì thêm.

An có một xâu ký tự ~S~ có độ dài ~N~, chỉ gồm các chữ cái Latin in thường. An muốn tìm một xâu con liên tiếp không rỗng của xâu ~S~ sao cho chênh lệch giữa số lần ký tự xuất hiện nhiều nhất và số lần ký tự xuất hiện ít nhất ở trong xâu con là lớn nhất. Lưu ý rằng, ký tự xuất hiện ít nhất phải xuất hiện ít nhất một lần trong xâu con.

Dữ liệu vào từ file văn bản CHENHLECH.INP:

• Dòng đầu tiên chứa số nguyên ~N~ ~(1\le N\le 10^6)~ là độ dài của xâu ~S~;
• Dòng thứ hai chứa xâu ~S~.

Kết quả ghi ra file văn bản CHENHLECH.OUT:

Một số nguyên duy nhất là chênh lệch lớn nhất của xâu con tìm được.

Ví dụ

Input

6
caabac

Output

2

Giải thích

Có thể chọn xâu con: aaba hoặc caaba hoặc aabac hoặc caabac.

Input

3
ttt

Output

0

Giải thích

Có thể chọn xâu con: ttt hoặc tt hoặc t.

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thoả mãn: ~N \le 10^2~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thoả mãn: ~N \le 10^5~;
• ~30\%~ số test còn lại ứng với ~30\%~ số điểm của bài không có ràng buộc gì thêm.