Cho ba số nguyên không âm ~N, K, X~. Với dãy số ~0, 1, 2, 3, ..., N~ người ta sắp xếp lại dãy số đó theo quy tắc:

• Đầu tiên là bộ các số chia ~K~ dư ~X~;
• Tiếp theo là bộ các số chia ~K~ dư ~X+1~;
• ~...~
• Tiếp theo là bộ các số chia ~K~ dư ~K-1~;
• Tiếp theo là bộ các số chia hết cho ~K~;
• Tiếp theo là bộ các số chia ~K~ dư ~1~;
• ~...~
• Cuối cùng là bộ các số chia ~K~ dư ~X-1~.

Trong mỗi bộ số có cùng tính chia hết, các số được sắp xếp giảm dần.

Ví dụ: ~N=10, K=4, X=2~.

• Ta có: bộ các số chia ~4~ dư ~2~ là ~10, 6, 2~; bộ các số chia ~4~ dư ~3~ là ~7, 3~; bộ các số chia hết cho ~4~ là ~8, 4, 0~; bộ các số chia ~4~ dư ~1~ là ~9, 5, 1~;
• Dãy số sau khi sắp xếp là: ~10, 6, 2, 7, 3, 8, 4, 0, 9, 5, 1~.

Yêu cầu: Cho ~Q~ truy vấn, mỗi truy vấn chứa ba số nguyên không âm ~N, K, X~ và số nguyên dương ~D~. Tìm số thứ ~D~ của dãy số sau khi sắp xếp.

Dữ liệu vào từ tệp văn bản DCH.INP:

• Dòng đầu tiên chứa số nguyên dương ~Q~ không vượt quá ~10^6~ là số lượng truy vấn;
• ~Q~ dòng tiếp theo: Mỗi dòng mô tả một truy vấn gồm bốn số ~N, K, X, D~ ~(0 \le X \lt K \lt N \le 10^{18}, D \le N + 1)~.

Dữ liệu ghi ra tệp văn bản DCH.OUT:

Gồm ~Q~ dòng, mỗi dòng chứa kết quả của một truy vấn.

Ví dụ

Input

2
10 4 2 5
10 3 0 6

Output

3
7

Giải thích

Trong truy vấn thứ hai: ~N=10, K=3, X=0~

• Dãy số sau khi sắp xếp là: ~9, 6, 3, 0, 7, 4, 1, 8, 5, 2~;
• Số thứ ~6~ là ~7~.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm thoả mãn: ~Q, N \le 10^3~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~X=0, Q\le 10^5~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho một xâu ~S~ chỉ gồm các chữ cái tiếng Anh in thường. Các chữ cái a, b, ..., z lần lượt được đánh số thứ tự là ~1, 2, ..., 26~. Trọng số của một xâu được định nghĩa là tổng các giá trị tuyệt đối của hiệu số thứ tự giữa các ký tự trong xâu với ký tự đầu tiên của xâu đó.

Ví dụ, với xâu cadc, trọng số của xâu là: ~|'c'-'c'|+|'a'-'c'|+|'d'-'c'|+|'c'-'c'|=|3-3|+|1-3|+|4-3|+|3-3|=0+2+1+0=3~.

Yêu cầu: Hãy tìm một xâu con gồm các ký tự liên tiếp thuộc ~S~ có trọng số lớn nhất và có ký tự đầu trùng với ký tự cuối.

Dữ liệu vào từ tệp văn bản TSX.INP:

Gồm một xâu ký tự có độ dài là ~N~ ~(N \le 10^6)~.

Dữ liệu ghi ra tệp văn bản TSX.OUT:

Một số nguyên là trọng số lớn nhất của xâu con thoả mãn.

Ví dụ

Input

bcacadbac

Output

8

Giải thích

Chọn xâu con cacadbac.

Input

abcaczc

Output

25

Giải thích

Chọn xâu con caczc.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm thoả mãn: ~N\le 10^2~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~N\le 10^4~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho một dãy ~A~ gồm ~N~ số nguyên ~A_1, A_2, ..., A_N~ (các phần tử có giá trị từ ~1~ đến ~9~). Gọi ~S[L~...~R]~ là số nguyên được ghép bởi các số từ vị trí ~L~ đến vị trí ~R~ trong dãy ~A~, theo thứ tự từ trái sang phải. Ví dụ: với dãy ~A=[2,6,5,7,4]~ thì ~S[2~...~5]~ là số ~6574~.

Một số nguyên không âm được gọi là may mắn nếu như trong biểu diễn thập phân của số đó không chứa số ~13~. Ví dụ: các số may mắn là ~6, 12, 31, 103, ...~; các số không may mắn là ~13, 5713, 321321, ...~

Yêu cầu: Bạn cần thực hiện ~Q~ yêu cầu thuộc một trong hai loại sau:

• Loại ~1~: Đưa ra số lượng các số may mắn không vượt quá ~S[L~...~R]~;
• Loại ~2~: Thay giá trị phần tử thứ ~i~ bằng giá trị ~X~.

Dữ liệu vào từ tệp văn bản SMM.INP:

• Dòng đầu tiên chứa hai số nguyên dương ~N, Q~ ~(N, Q\le 2 \times 10^5)~;
• Dòng thứ hai gồm ~N~ số nguyên ~A_1, A_2, ..., A_N~ viết liền nhau ~(1 \le A_i \le 9; 1\le i \le N)~;
• ~Q~ dòng tiếp theo, mỗi dòng chứa một yêu cầu thuộc một trong hai dạng sau:
  • 1 L R: Mô tả yêu cầu ghi ra số lượng số may mắn không vượt quá ~S[L~...~R]~ ~(1 \le L \le R \le N)~ sau khi chia dư cho ~10^9+7~;
  • 2 i X: Mô tả yêu cầu thay giá trị phần tử thứ ~i~ bằng giá trị ~X~ ~(1 \le i \le N; 1 \le X \le 9)~.

Dữ liệu ghi ra tệp văn bản SMM.OUT:

Với mỗi yêu cầu loại ~1~, ghi ra kết quả trên một dòng.

Ví dụ

Input

6 3
849613
1 1 2
2 3 4
1 4 4

Output

84
7

Giải thích

Với yêu cầu đầu tiên, các số may mắn không vượt quá ~84~ là ~0, 1, 2, ..., 12, 14, 15, ..., 84~.

Với yêu cầu thứ hai, dãy ~A~ là ~844613~.

Với yêu cầu thứ ba, các số may mắn không vượt quá ~6~ là ~0, 1, 2, ..., 5, 6~.

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm thoả mãn: ~N\le 6; Q=1~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N\le 6~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N\le 100~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~Q\le 2000~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

TR là một hệ thống trao đổi dữ liệu trực tiếp giữa các máy tính đang được thử nghiệm tại trường ~X~. Trường có ~N~ máy tính được đánh số từ ~1~ đến ~N~. Các máy tính đều sử dụng hệ thống TR và được kết nối với nhau theo đồ thị dạng cây.

Ban đầu, hệ thống có một tệp dữ liệu đang được lưu trữ bởi một hoặc hai máy tính. Trường muốn truyền tệp này đến tất cả các máy tính khác trong hệ thống. Cơ chế truyền dữ liệu của hệ thống TR như sau: cứ một phút, mỗi máy tính trong hệ thống chỉ có thể truyền dữ liệu đến duy nhất một máy tính khác được kết nối trực tiếp với nó.

Yêu cầu: Cho số hiệu của các máy tính đang lưu trữ tệp dữ liệu ở thời điểm ban đầu. Hãy tính thời gian tối thiểu để tất cả các máy tính trong hệ thống nhận được tệp dữ liệu.

Dữ liệu vào từ tệp văn bản TDL.INP:

• Dòng đầu tiên chứa số nguyên ~N~ ~(1 \lt N \le 10^5)~ là số lượng máy tính;
• ~N-1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên khác nhau ~x~ và ~y~ ~(1 \le x, y \le N)~ mô tả số hiệu của hai máy tính được kết nối trực tiếp;
• Dòng tiếp theo chứa số ~M~ ~(1\le M\le 2)~ là số lượng máy tính đang lưu trữ tệp dữ liệu ở thời điểm ban đầu;
• Dòng tiếp theo chứa ~M~ số nguyên dương mô tả số hiệu của các máy tính đang lưu trữ tệp dữ liệu ở thời điểm ban đầu;

Dữ liệu ghi ra tệp văn bản TDL.OUT:

Gồm một số nguyên là thời gian tối thiểu hoàn thành công việc.

Ví dụ

Input

6
1 2
2 3
2 4
1 5
5 6
1

Output

3

Giải thích

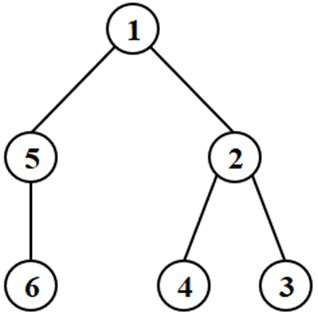
Ban đầu máy ~1~ lưu trữ tệp dữ liệu.

Phút thứ ~1~: máy ~2~ nhận được tệp dữ liệu.

Phút thứ ~2~: máy ~3~ và ~5~ nhận được tệp dữ liệu.

Phút thứ ~3~: máy ~4~ và ~6~ nhận được tệp dữ liệu.

Input

6
1 2
2 3
2 4
1 5
5 6
2
1 2

Output

2

Giải thích

Ban đầu máy ~1~ và ~2~ lưu trữ tệp dữ liệu.

Phút thứ ~2~: máy ~3~ và ~5~ nhận được tệp dữ liệu.

Phút thứ ~3~: máy ~4~ và ~6~ nhận được tệp dữ liệu.

Minh hoạ

Ràng buộc

• Có ~25\%~ số test ứng với ~25\%~ số điểm có ~N\le 20~;
• ~25\%~ số test khác ứng với ~25\%~ số điểm có ~M=1~;
• ~25\%~ số test khác ứng với ~25\%~ số điểm có ~M=2; N\le 1000~;
• ~25\%~ số test còn lại ứng với ~25\%~ số điểm không có ràng buộc gì thêm.

Cho số nguyên dương ~N~. Hãy tìm ra dãy số thoả mãn:

• Số lượng các phần tử lớn hơn ~2~, tất cả phần tử của dãy là số nguyên dương;
• Dãy số là dãy tăng dần vè chênh lệch giữa hai phần tử liên tiếp bằng nhau;
• Tổng tất cả các phần tử của dãy số là ~N~;
• Nếu có nhiều dãy có tổng bằng ~N~, tìm ra dãy có số lượng phần tử lớn nhất;
• Nếu có nhiều hơn một dãy thoả mãn, chọn dãy có phần tử đầu tiên là bé nhất.

Dữ liệu vào từ tệp văn bản DCD.INP:

Một dòng duy nhất chứa số nguyên dương ~N~ ~(N \le 10^9)~.

Dữ liệu ghi ra tệp văn bản DCH.OUT:

Gồm một dòng là dãy số thoả mãn. Nếu không có dãy số thoả mãn, ghi ra ~-1~.

Ví dụ

Input

12

Output

1 4 7

Giải thích

Dãy ~2, 4, 6~ hoặc ~3, 4, 5~ cũng có tổng là ~12~ và số lượng phần tử là ~3~. Nhưng dãy số ~1, 4, 7~ là dãy có phần tử đầu tiên bé nhất.

Input

20

Output

2 3 4 5 6

Giải thích

Dãy ~2, 4, 6, 8~ cũng có tổng là ~20~ và số lượng phần tử là ~4~. Nhưng dãy số ~2, 3, 4, 5, 6~ là dãy có số lượng phần tử lớn hơn.

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm thoả mãn: ~N \le 10^3~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~N \le 10^5~;
• ~30\%~ số test còn lại ứng với ~30\%~ số điểm không có ràng buộc gì thêm.

Cho một tập ~S~ gồm ~N~ xâu ký tự ~S_1, S_2, ..., S_N~. Mỗi xâu trong tập ~S~ chỉ chứa các chữ cái tiếng Anh in thường. Với xâu ~S_i~ ~(1\le i\le N)~, chọn ra một xâu con không rỗng gồm các ký tự liên tiếp, gọi xâu con đó là ~T_i~. Sau đó, nối các xâu ~T_1, T_2, ..., T_N~ theo thứ tự từ trái qua phải tạo thành xâu ~P~.

Yêu cầu: Cho số nguyên dương ~K~, hãy tìm xâu ~P~ có độ dài đúng bằng ~K~ và có thứ tự từ điển nhỏ nhất.

Dữ liệu vào từ tệp văn bản NX.INP:

• Dòng đầu tiên chứa hai số nguyên ~N~ và ~K~ lần lượt là số lượng xâu trong tập ~S~ và độ dài xâu ~P~.
• ~N~ dòng tiếp theo, dòng thứ ~i~ ~(1\le i\le N)~ chứa xâu ký tự ~S_i~;

Dữ liệu đảm bảo ~1\le N\le K\le \displaystyle\sum^N_{i=1}|S_i|\le 4000~ với ~|S_i|~ là độ dài của xâu ~S_i~.

Dữ liệu ghi ra tệp văn bản NX.OUT:

Gồm một dòng là xâu ~P~ cần tìm.

Ví dụ

Input

2 3
aen
bbb

Output

abb

Giải thích

Chọn ra xâu con a của xâu aen.

Chọn ra xâu con bb của xâu bbb.

Input

2 3
bb
adh

Output

bad

Giải thích

Chọn ra xâu con b của xâu bb.

Chọn ra xâu con ad của xâu adh.

Ràng buộc

• Có ~30\%~ số test ứng với ~30\%~ số điểm thoả mãn: ~N=2; \ |S_1|, |S_2| \le 100~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~1\le N\le 50; \ |S_1|=|S_i|\le 10~ ~(1\le i \le N)~;
• ~40\%~ số test còn lại ứng với ~40\%~ số điểm không có ràng buộc gì thêm.

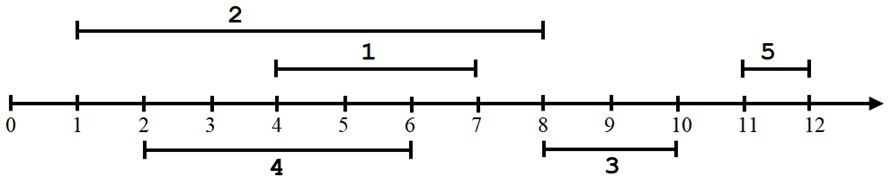
Cho ~N~ đoạn thẳng song song với trục ~Ox~, các đoạn thẳng được đánh số từ ~1~ đến ~N~. Đoạn thẳng thứ ~i~ ~(1\le i\le N)~ được xác định bởi điểm đầu và điểm cuối lần lượt là hai số nguyên dương ~l_i, r_i~. Hai đoạn thẳng ~i, j~ ~(1\le i, j\le N)~ được gọi là giao nhau khi: ~(r_i-l_i)+(r_j-l_j)\ge \max(r_i, r_j) - \min(l_i, l_j)~.

Ví dụ: như hình vẽ dưới, đoạn thẳng thứ ~1~ và ~4~, đoạn thẳng thứ ~2~ và ~3~, ... được gọi là giao nhau; đoạn thẳng thứ ~2~ và ~5~, đoạn thẳng thứ ~1~ và ~3~, ... không được gọi là giao nhau.

Yêu cầu: Hãy chọn ra hai tập đoạn thẳng ~S_1~ (có số lượng phần tử là ~x~) và ~S_2~ (có số lượng phần tử là ~y~) thoả mãn:

• Mỗi đoạn thẳng trong ~N~ đoạn thẳng thuộc tối đa một tập;
• Các đoạn thẳng trong cùng một tập đôi một giao nhau;
• ~x\ge y~ và ~y~ lớn nhất.

Dữ liệu vào từ tệp văn bản CT.INP:

• Dòng đầu chứa số nguyên dương ~N~ ~(2\le N\le 5 \times 10^5)~ là số lượng đoạn thẳng;
• ~N~ dòng tiếp theo, dòng thứ ~i~ ~(1\le i\le N)~ chứa hai số ~l_i, r_i~ ~(1\le l_i\le r_i\le 10^9)~ mô tả điểm đầu và điểm cuối của đoạn thẳng thứ ~i~.

Dữ liệu ghi ra tệp văn bản CT.OUT:

Ghi ra giá trị ~y~ thoả mãn.

Ví dụ

Input

5
4 7
1 8
8 10
2 6
11 12

Output

2

Giải thích

Có thể có nhiều cách lựa chọn ra hai tập.

Nếu chọn tập ~S_1~ gồm ~3~ đoạn thẳng thứ ~1, 2~ và ~4~; tập ~S_2~ gồm ~1~ đoạn thẳng thứ ~3~ hoặc ~5~; cách này có ~x=3, y=1~.

Nếu chọn tập ~S_1~ gồm ~2~ đoạn thẳng thứ ~1~ và ~4~; tập ~S_2~ gồm ~2~ đoạn thẳng thứ ~2~ và ~3~; cách này có ~x=2, y=2~.

Ràng buộc

• Có ~25\%~ số test ứng với ~25\%~ số điểm thoả mãn: ~N\le 500~;
• ~25\%~ số test khác ứng với ~25\%~ số điểm thoả mãn: ~N\le 5000~;
• ~25\%~ số test khác ứng với ~25\%~ số điểm thoả mãn: ~N\le 10^5~;
• ~25\%~ số test còn lại ứng với ~25\%~ số điểm không có ràng buộc gì thêm.