Cho một dải ô gồm ~10^9~ ô vuông liên tiếp, trong đó có ~n~ ô chưa được sơn màu và những ô còn lại đã được sơn. Một cây cọ sơn kích thước ~w~ có thể quét sơn cho ~w~ ô liên tiếp, cụ thể là nếu chọn ~x~ (~1 \leq x \leq 10^9~) là vị trí bắt đầu thì cây cọ có thể quét sơn toàn bộ các ô liên tiếp từ vị trí ~x~ đến ~x + w - 1~ (có thể quét ra ngoài, không ảnh hưởng đến bài toán).

Bạn đang lên kế hoạch để sơn hết các ô chưa được sơn. Bạn dự định mua ~a~ cây cọ sơn kích thước ~w~ và ~b~ cây cọ sơn kích thước ~2 \times w~, mỗi cây cọ sẽ được dùng để sơn nhiều nhất một lần và mỗi ô có thể được sơn nhiều lần. Nhưng cây cọ có kích thước càng lớn thì giá cả lại càng cao, vì vậy bạn muốn tìm giá trị ~w~ nhỏ nhất có thể. Hãy tìm giá trị ~w~ đó.

Input

• Dòng đầu tiên chứa ba số nguyên ~n~, ~a~ và ~b~ ~(1 \leq n \leq 2000, 0 \leq a, b \leq 10^9, a + b \geq 1)~ lần lượt là số ô chưa được tô màu, số cây cọ sơn kích thước ~w~ và ~2 \times w~.
• Dòng tiếp theo chứa ~n~ số nguyên phân biệt ~x_1, x_2, \ldots, x_n~ ~(1 \leq x_i \leq 10^9)~ là vị trí của những ô chưa được sơn.

Output

• Một số nguyên duy nhất là giá trị ~w~ nhỏ nhất để có thể sơn hết những ô chưa được sơn.

Scoring

• Subtask ~1~ (~20\%~ số điểm): Các ô chưa được sơn đứng cạnh nhau.
• Subtask ~2~ (~20\%~ số điểm): ~b = 0~.
• Subtask ~3~ (~30\%~ số điểm): ~n \leq 200~.
• Subtask ~4~ (~30\%~ số điểm): Không có ràng buộc gì thêm.

Example

Test 1

Input

5 1 1
1 2 3 4 5

Output

2

Note

• Cây cọ kích thước ~2~ sơn các ô từ vị trí ~1~ đến vị trí ~2~.
• Cây cọ kích thước ~4~ sơn các ô từ vị trí ~2~ đến vị trí ~5~.

Test 2

Input

7 3 0
1 3 4 5 7 9 10

Output

4

Thành phố XYZ bị một dòng sông chia cắt thành hai vùng là A và B. Mỗi vùng bao gồm dòng sông và một dãy toà nhà chạy dọc theo bờ sông, được đánh số từ ~0~ đến ~10^9~. Khoảng cách giữa hai toà nhà kề nhau là ~1~ đơn vị, và bề rộng dòng sông cũng bằng ~1~ đơn vị. Toà nhà ~i~ ở vùng A luôn đối diện với toà nhà ~i~ ở vùng B.

Có ~N~ công dân sinh sống và làm việc trong thành phố. Công dân ~i~ sống ở vùng ~P_i~ tại toà nhà ~S_i~ và làm việc ở vùng ~Q_i~ tại toà nhà ~T_i~. Hiện tại họ phải qua sông bằng thuyền, nên chính phủ quyết định xây dựng ~K~ cây cầu để người dân có thể đi lại bằng xe.

Mỗi cây cầu phải được đặt giữa đúng hai toà nhà đối diện nhau và phải vuông góc với dòng sông. Các cây cầu không được chồng lên nhau.

Ký hiệu ~D_i~ là khoảng cách nhỏ nhất mà công dân ~i~ phải di chuyển từ nhà đến nơi làm việc sau khi xây dựng ~K~ cây cầu.

Yêu cầu: Tìm phương án xây dựng ~K~ cây cầu sao cho tổng ~D_1 + D_2 + \dots + D_N~ là nhỏ nhất.

Input

• Dòng đầu chứa hai số nguyên ~K~ và ~N~ (~K \le 2~; ~1 \le N \le 10^5~).
• Mỗi trong ~N~ dòng tiếp theo chứa bốn giá trị ~P_i, S_i, Q_i, T_i~:
  • ~P_i \in \{A, B\}~, ~S_i~ là toà nhà (~0 \le S_i \le 10^9~).
  • ~Q_i \in \{A, B\}~, ~T_i~ là toà nhà (~0 \le T_i \le 10^9~).
• Có thể có nhiều công dân có nhà hoặc nơi làm việc trùng cùng một toà nhà.

Output

• In ra một số nguyên duy nhất — tổng khoảng cách nhỏ nhất.

Subtasks

• 25%: ~K = 1~, ~1 \le N \le 10^3~
• 25%: ~K = 1~, ~1 \le N \le 10^5~
• 25%: ~K = 2~, ~1 \le N \le 10^3~
• 25%: ~K = 2~, ~1 \le N \le 10^5~

Sample Test

Input 1

1 5
B 0 A 4
B 1 B 3
A 5 B 7
B 2 A 6
B 1 A 7

Output 1

24

Input 2

2 5
B 0 A 4
B 1 B 3
A 5 B 7
B 2 A 6
B 1 A 7

Output 2

22

Trò chơi diễn ra trên bảng ô vuông kích thước ~m \times n~, các hàng của bảng được đánh số từ ~1~ đến ~m~ (từ trên xuống dưới), các cột của bảng được đánh số từ ~1~ đến ~n~ (từ trái sang phải). Ô giao giữa hàng ~i~ và cột ~j~ được gọi là ô ~(i, j)~. Trên bảng có ~k~ ô có chứa quà. Người chơi xuất phát tại ô ~(1, 1)~ và di chuyển đến ô ~(m, n)~. Mỗi bước đi, người chơi chỉ có thể đi sang ô kề cạnh ở cột bên phải hoặc đi xuống ô kề cạnh ở dòng dưới. Khi đi vào ô chứa quà, người chơi sẽ được nhận quà tại ô đó. Nhiệm vụ của người chơi là tìm cách đi để nhận được nhiều quà nhất.

Một ô chứa quà được gọi là vị trí quan trọng, nếu bỏ quà tại ô đó thì số lượng quà nhiều nhất mà người chơi thu được bị giảm đi ~1~.

Yêu cầu: Cho ~m, n~ là kích thước của bảng và vị trí ~k~ ô đặt quà. Hãy đếm số lượng ô được gọi là quan trọng.

Dữ liệu: Vào từ thiết bị vào chuẩn gồm hai dòng:

• Dòng đầu chứa ba số nguyên ~m, n, k~ (~m, n \le 10^9; k \le 10^5~);
• ~k~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~x, y~ (~1 \le x \le m; 1 \le y \le n~) mô tả vị trí các ô chứa quà, các ô phân biệt (không có nhiều hơn một quà ở cùng một ô).

Kết quả: Ghi ra thiết bị ra chuẩn một số nguyên duy nhất là số lượng ô được gọi là vị trí quan trọng.

Ví dụ:

Dữ liệu	Kết quả	Giải thích
4 5 3 2 1 1 5 4 4	2	Có hai vị trí quan trọng là ô (2, 1) và ô (4, 4) .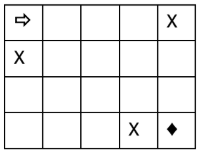

Ràng buộc:

• Có ~40\%~ số test tương ứng với ~40\%~ số điểm có ~m, n \le 100; k \le 100~;
• ~30\%~ số test khác tương ứng với ~30\%~ số điểm có ~m, n \le 10^6; k \le 1000~;
• ~30\%~ số test còn lại tương ứng với ~30\%~ số điểm không có ràng buộc gì thêm.

Biểu thức ngoặc là xâu chỉ gồm các kí tự '(', ')', '[', ']', '{', '}'. Biểu thức ngoặc đúng và bậc của biểu thức ngoặc đúng được định nghĩa một cách đệ quy như sau:

• Biểu thức rỗng là biểu thức ngoặc đúng và có bậc bằng ~0~.
• Nếu ~A~ là biểu thức ngoặc đúng có bậc bằng ~k~ thì (A), [A], {A} cũng là một biểu thức ngoặc đúng có bậc bằng ~k \; + \; 1~.
• Nếu ~A~ và ~B~ là hai biểu thức ngoặc đúng và có bậc tương ứng là ~k_1~ và ~k_2~ thì ~AB~ cũng là một biểu thức ngoặc đúng có bậc bằng ~\text{max}(k_1, \; k_2)~.

Ví dụ, ()[()] là một biểu thức ngoặc đúng có bậc bằng ~2~ còn {()[{}]} là một biểu thức ngoặc đúng và có bậc bằng ~3~. Ta sẽ xét hai trường hợp sau:

• ~T \; = \; 1~: biểu thức ngoặc chỉ gồm kí tự '(' và ')'.
• ~T \; = \; 2~: biểu thức ngoặc gồm kí tự '(', ')', '[', ']', '{', '}'.

Với hai số nguyên ~N~, ~K~, người ta tiến hành tạo ra tất cả các biểu thức ngoặc đúng có độ dài ~N~ và bậc không vượt quá ~K~. Sắp xếp các biểu thức ngoặc theo thứ tự từ điển, chú ý rằng '(' < ')' < '[' < ']' < '{' < '}'.

Cho biểu thức ngoặc đúng ~S~, hãy tìm thứ tự của biểu thức ngoặc đúng ~S~.

Input:

• Dòng thứ nhất chứa số nguyên ~T~ ~(1 \leq T \leq 2)~.
• Dòng thứ hai chứa hai số nguyên ~N~ và ~K~ ~(N \leq 3000 \; K \leq N / 2)~.
• Dòng thứ ba chứa ~N~ kí tự của biểu thức ngoặc ~S~.

Output:

• Thứ tự của dãy ngoặc ~S~ lấy dư cho ~10^9 + 7~.

Sample test

Input:

2
8 4
{}(({}))

Output:

1008

Subtask:

• Subtask ~1~ (~20\%~ số điểm): ~T \; = \; 2, \; N \; \leq \; 10~.
• Subtask ~2~ (~15\%~ số điểm): ~T \; = \; 1, \; S \; =~ ()()()...
• Subtask ~3~ (~15\%~ số điểm): ~T \; = \; 2, \; S \; =~ {}{}{}...
• Subtask ~4~ (~25\%~ số điểm): ~T \; = \; 1~.
• Subtask ~5~ (~25\%~ số điểm): ~T \; = \; 2~.

Cho dãy số nguyên ~n~ phần tử ~a_1, a_2, ..., a_n~, trả lời các truy vấn như sau:

• xét đoạn liên tiếp từ ~l~ đến ~r~
• với mỗi cặp ~(x, y)~ mà ~l\le x\le y\le r~ tính khoảng cách hamming của hai dãy ~\{a_x, a_{x + 1}, ..., a_y\}~ và dãy ~\{a_l, a_{l + 1}, ..., a_{l + y - x}\}~
• tính tổng khoảng cách hamming của tất cả các cặp ~(x, y)~

Input

• Dòng đầu chứa hai số ~n, q~ (~1\le n, q\le 2\cdot 10^5~)

• Dòng hai chứa ~n~ số ~a_i~ (~1\le a_i\le 10^6~)

• ~q~ dòng tiếp theo mỗi dòng chứa hai số ~l, r~ mô tả các truy vấn

Output

• Ghi ra ~q~ dòng tương ứng với kết quả của các truy vấn.

Example

Sample Input

4 4
1 2 1 3
1 1
2 3
2 4
1 4

Sample Output

0
1
4
8