Cho một số nguyên không âm ~k~ ~(0 \leq k \leq 9)~. Ban đầu, bạn có một xâu ~S~ độ dài ~1~, chứa đúng một chữ số ~s~ ~(0 \leq s \leq k)~.

Phép biến đổi đồng thời trên toàn bộ xâu được định nghĩa như sau — mỗi bước biến đổi áp dụng cùng lúc cho tất cả các chữ số hiện có:

• Nếu chữ số là ~d~ với ~0 \leq d < k~, thì nó biến thành chữ số ~d + 1~.
• Nếu chữ số là ~k~, thì nó được thay thế bởi dãy các chữ số ~k, k - 1, k - 2, \ldots, 1, 0~ (tức là dãy giảm dần từ ~k~ về ~0~).

Sau đó, bạn cần xử lý ~q~ truy vấn độc lập. Mỗi truy vấn cho ~5~ số nguyên ~s, n, l, r, v~ và yêu cầu:

• Giả sử ban đầu xâu ~S~ chỉ chứa chữ số ~s~.
• Sau ~n~ lần biến đổi, hãy cho biết trong đoạn con từ vị trí ~l~ đến ~r~ (đánh số từ ~1~), có bao nhiêu chữ số bằng ~v~.

Các truy vấn độc lập, nghĩa là bạn luôn bắt đầu lại từ xâu có độ dài ~1~ chứa chữ số ~s~ tương ứng với truy vấn đó.

Input (TRANSSEQ.INP)

• Dòng đầu tiên chứa hai số nguyên ~k~ và ~q~ (~0 \leq k \leq 9~, ~1 \leq q \leq 10^5~).
• Mỗi trong ~q~ dòng tiếp theo chứa ~5~ số nguyên: ~s, n, l, r~ và ~v~, trong đó:
  • ~0 \leq s \leq k~ — chữ số ban đầu.
  • ~0 \leq n \leq 10^{18}~ — số lần biến đổi.
  • ~1 \leq l \leq r \leq \min~ (độ dài của xâu sau ~n~ lần biến đổi, ~10^{18}~) (Độ dài của xâu sau mỗi phép biến đổi luôn hữu hạn vì ~k \leq 9~ và ~n~ hữu hạn.)
  • ~0 \leq v \leq k~.

Output (TRANSSEQ.OUT)

• Với mỗi truy vấn, in ra một dòng duy nhất — số lượng chữ số ~v~ xuất hiện trong đoạn ~[l, r]~ của xâu sau ~n~ lần biến đổi.

Scoring

• Subtask ~1~ (~20\%~ số điểm): ~n \leq 5~.
• Subtask ~2~ (~25\%~ số điểm): ~k = 1, s = 0, n \leq 30~.
• Subtask ~3~ (~25\%~ số điểm): ~k = 1, s = 0~.
• Subtask ~4~ (~30\%~ số điểm): không có ràng buộc thêm.

Examples

TRANSSEQ.INP

2 4
2 0 1 1 2
2 1 1 3 1
2 2 2 4 2
1 3 1 5 0

TRANSSEQ.OUT

1
1
1
1

Explanation

• Truy vấn 1: ~s = 2, n = 0 \rightarrow~ ta có xâu ~S =~ 2, đoạn ~[1, 1] = ~ 2 có ~1~ chữ số ~2~.
• Truy vấn 2: ~s = 2, n = 1 \rightarrow~ ta có chuỗi biến đổi là 2 ~\rightarrow~ 210, đoạn ~[1, 3] = ~ 210 có ~1~ chữ số ~1~.
• Truy vấn 3: ~s = 2, n = 2 \rightarrow~ ta có chuỗi biến đổi là 2 ~\rightarrow~ 210 ~\rightarrow~ 21021, đoạn ~[2, 4]~ = 102, có ~1~ chữ số ~2~.
• Truy vấn 4: ~s = 1, n = 3 \rightarrow~ ta có chuỗi biến đổi là 1 ~\rightarrow~ 2 ~\rightarrow~ 210 ~\rightarrow~ 21021, đoạn ~[1, 5] = ~ 21021 có ~1~ chữ số ~0~.

Một công ty có ~n~ nhân viên làm việc từ xa. Các nhân viên được đánh số từ ~1~ đến ~n~ và được tổ chức theo cấu trúc quản lý dạng cây như sau:

• Nhân viên ~1~ là giám đốc, là gốc của cây.
• Mỗi nhân viên khác có đúng một người quản lý trực tiếp.
• Mộĩ người quản lý các nhân viên do mình quản lý trực tiếp và tất cả nhân viên dưới quyền của họ đều là nhân viên của người quản lý đó.

Mỗi nhân viên sinh sống tại một địa phương, ký hiệu địa phương của nhân viên ~i~ là ~c_{i}~.

Công ty chuẩn bị xây dựng văn phòng offline để triển khai một dự án lớn. Để lựa chọn địa điểm và đội ngũ dự án, công ty tiến hành hai bước:

1. Chọn người quản lý — chọn một nhân viên ~u~. Văn phòng sẽ đặt tại địa phương của người quản lý.
2. Sắp xếp lại đội ngũ — được phép hoán đổi team giữa hai nhân viên cùng cấp (cùng độ sâu trong cây). Nếu hai nhân viên cùng độ sâu đổi team cho nhau, toàn bộ các quan hệ "sếp - nhân viên" của họ cũng hoán đổi tương ứng. Có thể thực hiện nhiều lần hoán đổi. Ví dụ: nếu hai nhân viên ở cùng độ sâu là ~4~ và ~7~ đổi team, thì toàn bộ các nhân viên dưới quyền của ~4~ sẽ trở thành dưới quyền của ~7~ và ngược lại.

Mục tiêu: sau khi sắp xếp tối ưu, người lãnh đạo ~u~ có nhiều nhân viên thuộc sự quản lý của mình cùng địa phương với mình nhất.

Input (OFFOFF.INP)

• Dòng đầu tiên chứa một số nguyên dương ~n~ ~(1 \leq n \leq 10^5)~ là số lượng nhân viên.
• Dòng thứ hai chứa ~n~ số nguyên dương ~c_1, c_2, \ldots, c_n~ ~(1 \leq c_{i} \leq n)~ — địa phương của từng nhân viên.
• Dòng thứ ba chứa ~n-1~ số nguyên dương ~p_2, p_3, \ldots, p_n~ ~(1 \leq p_{i} \leq n)~, trong đó ~p_i~ là quản lý trực tiếp của nhân viên ~i~.

Output (OFFOFF.OUT)

• Dòng duy nhất gồm hai số nguyên dương cách nhau bởi một dấu cách:
  • Số lượng nhân viên cùng địa phương tối đa mà người lãnh đạo quản lý (tính cả người lãnh đạo).
  • Số thao tác hoán đổi ít nhất cần để đạt được kết quả tối ưu.

Scoring

• Subtask ~1~ (~20\%~ số điểm): mỗi người có tối đa một nhân viên do mình quản lý trực tiếp.
• Subtask ~2~ (~25\%~ số điểm): ~n \leq 2000~.
• Subtask ~3~ (~25\%~ số điểm): có tối đa ~10~ nhân viên ở mỗi địa phương.
• Subtask ~4~ (~30\%~ số điểm): không có ràng buộc gì thêm.

Example

OFFOFF.INP

7
3 2 1 3 2 1 2
1 1 2 2 3 3

OFFOFF.OUT

3 1

Explanation

Cấu trúc công ty:

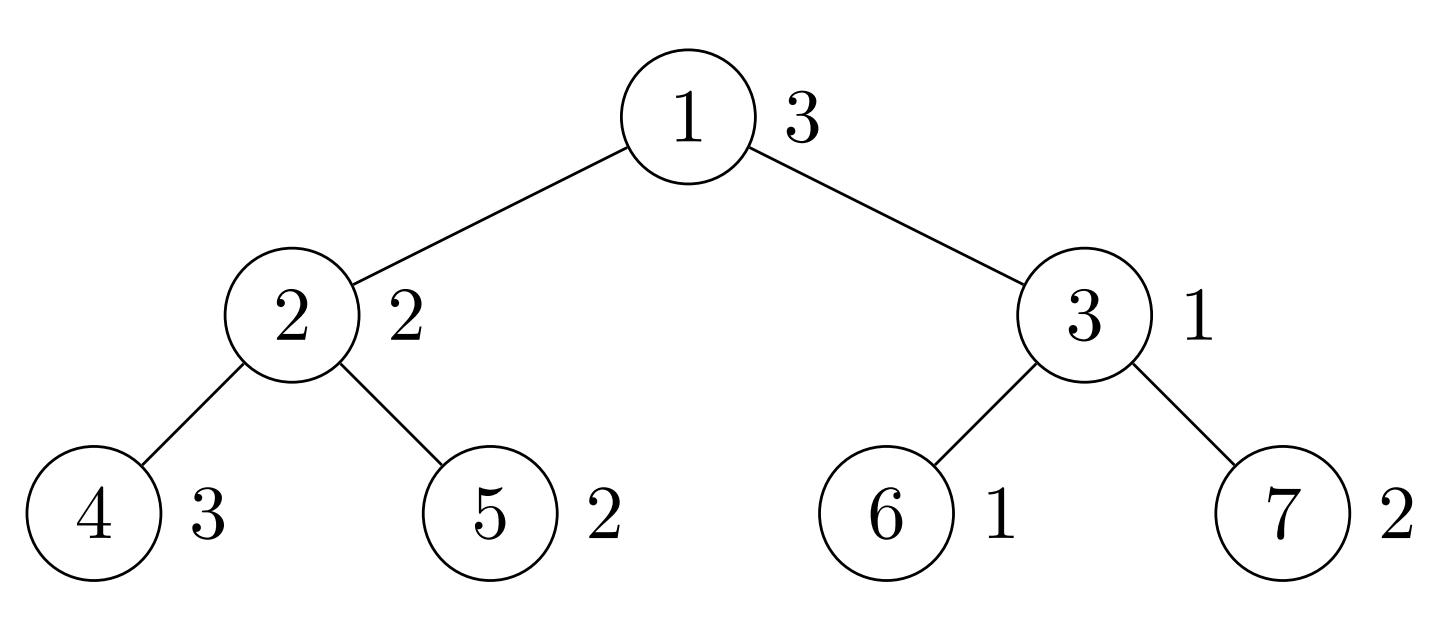
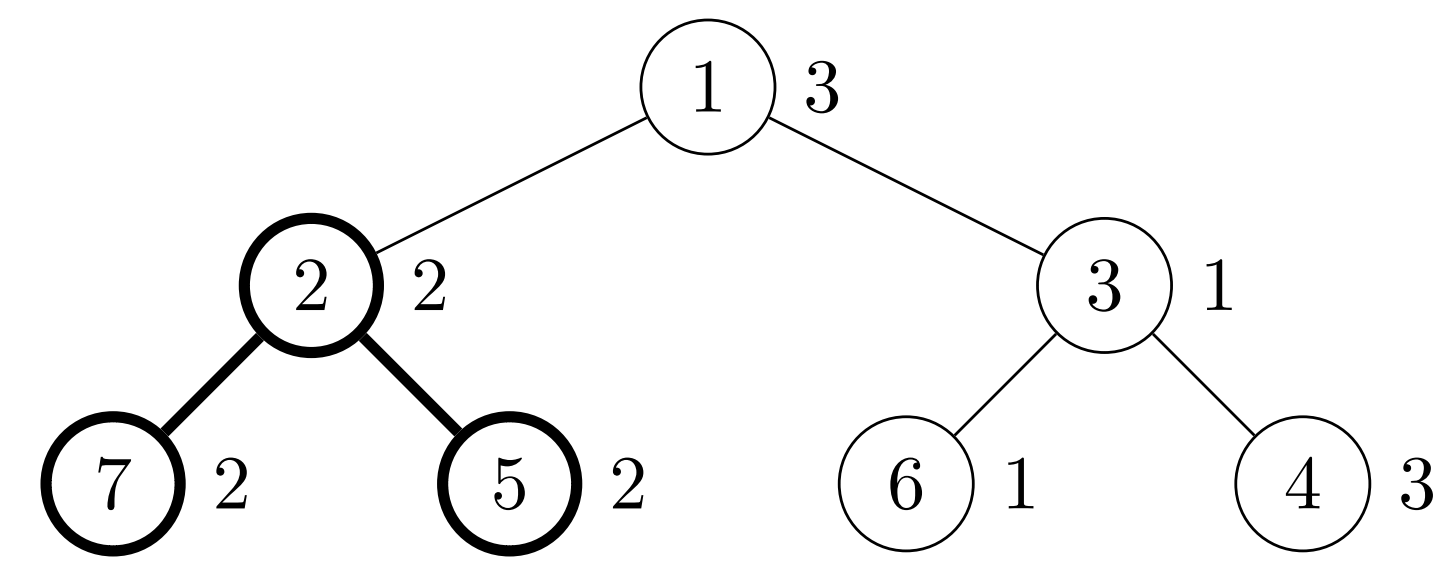
Chọn người lãnh đạo là nhân viên số ~2~ (địa phương ~2~). Hoán đổi nhân viên ~4~ và nhân viên ~7~ để đạt cấu hình tối ưu.

Cho một dãy số ~a_{0}, a_{1}, a_{2}, \ldots, a_{n - 1}~ có độ dài ~n~. Độ dài ~n~ của dãy số có dạng ~n = 2^{k}~ với ~k~ là một số nguyên dương.

Bạn hãy thực hiện ~q~ truy vấn trên dãy số này. Mỗi truy vấn thuộc một trong ba loại sau:

1. 1 x: với mọi số ~i~ từ ~0~ đến ~n - 1~, nếu ~i < (i \oplus x)~ thì hoán đổi ~a_{i}~ và ~a_{i \oplus x}~. Ở đây, ~\oplus~ là phép toán XOR.
2. 2 l r: tính tổng ~\sum_{i = l}^{r} a_{i} = a_{l} + a_{l + 1} + \ldots + a_{r}~.
3. 3 l r: tính tổng ~\sum_{i = l}^{r} (a_{i} \times (i - l + 1)) = a_{l} \times 1 + a_{l+1} \times 2 + \ldots + a_{r} \times (r - l + 1)~.

Với mỗi truy vấn loại 2 và loại 3, in ra kết quả trên một dòng riêng.

Input (XOREX.INP)

• Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~q~ ~(2 \leq n \leq 2^{19}, 1 \leq q \leq 2 \times 10^{5})~.
• Dòng thứ hai chứa ~n~ số nguyên ~a_{0}, a_{1}, a_{2}, \ldots, a_{n - 1}~ ~(0 \leq a_{i} \leq 10^{6})~.
• ~q~ dòng tiếp theo, mỗi dòng mô tả một truy vấn thuộc một trong ba loại:
  • ~1~ ~x~ ~(0 \leq x < n)~ thể hiện truy vấn loại 1.
  • ~2~ ~l~ ~r~ ~(0 \leq l \leq r < n)~ thể hiện truy vấn loại 2.
  • ~3~ ~l~ ~r~ ~(0 \leq l \leq r < n)~ thể hiện truy vấn loại 3.

Output (XOREX.OUT)

• Với mỗi truy vấn loại 2 và loại 3, in ra kết quả trên một dòng.

Scoring

• Subtask ~1~ (~6\%~ số điểm): ~n \leq 2^{10}, q \leq 10^{3}~.
• Subtask ~2~ (~8\%~ số điểm): không có truy vấn loại ~1~.
• Subtask ~3~ (~10\%~ số điểm): mọi truy vấn loại ~1~ đều diễn ra trước truy vấn loại ~2~ và loại ~3~.
• Subtask ~4~ (~20\%~ số điểm): không có truy vấn loại ~3~.
• Subtask ~5~ (~17\%~ số điểm): ~n \leq 2^{16}~.
• Subtask ~6~ (~19\%~ số điểm): ~l = 0, r = n - 1~ trong mọi truy vấn loại ~2~ và loại ~3~.
• Subtask ~7~ (~20\%~ số điểm): không có ràng buộc nào thêm.

Example

XOREX.INP

8 5
1 2 3 4 5 6 7 8
1 3
2 1 6
1 7
2 0 7
3 2 7

XOREX.OUT

27
36
73

Explanation

Trong truy vấn đầu tiên, ta hoán đổi các cặp ~(a_{0}, a_{3}), (a_{1}, a_{2}), (a_{4}, a_{7}), (a_{5}, a_{6})~. Dãy số sau khi thực hiện truy vấn này là ~[4, 3, 2, 1, 8, 7, 6, 5]~.

Trong truy vấn thứ hai, tổng từ ~a_{1}~ đến ~a_{6}~ là ~3 + 2 + 1 + 8 + 7 + 6 = 27~.

Trong truy vấn thứ ba, ta hoán đổi các cặp ~(a_{0}, a_{7}), (a_{1}, a_{6}), (a_{2}, a_{5}), (a_{3}, a_{4})~. Dãy số sau khi thực hiện truy vấn này là ~[5, 6, 7, 8, 1, 2, 3, 4]~.

Trong truy vấn thứ tư, tổng từ ~a_{0}~ đến ~a_{7}~ là ~5 + 6 + 7 + 8 + 1 + 2 + 3 + 4 = 36~.

Trong truy vấn thứ năm, tổng ~\sum_{i=2}^{7} (a_{i} \times (i - 2 + 1)) = a_{2} \times 1 + a_{3} \times 2 + a_{4} \times 3 + a_{5} \times 4 + a_{6} \times 5 + a_{7} \times 6 = 7 \times 1 + 8 \times 2 + 1 \times 3 + 2 \times 4 + 3 \times 5 + 4 \times 6 = 73~.