Cho dãy các số nguyên tố ~p_{1}, p_{2}, p_{3}, \ldots~ được sắp xếp tăng dần.

Với hai số nguyên tố liên tiếp ~p_i~ và ~p_{i+1}~, ta định nghĩa ~f(i)~ là số nhỏ nhất có dạng sau:

• Chia hết cho ~p_{i+1}~,
• Và khi viết ở dạng thập phân, phần đuôi (hậu tố) của số đó chính là ~p_{i}~.

Ví dụ:

• Với cặp ~(p_i, p_{i+1}) = (5, 7)~, ta có ~f(i) = 35~ (vì ~35~ chia hết cho ~7~ và có đuôi là ~5~).
• Với cặp ~(p_i, p_{i+1}) = (7, 11)~, ta có ~f(i) = 77~ (vì ~77~ chia hết cho ~11~ và có đuôi là ~7~).

Yêu cầu: cho hai số nguyên ~l~ và ~r~, hãy tính tổng:

$$ = f(i_{1}) + f(i_{2}) + \ldots + f(i_{k})$$

với tất cả các cặp số nguyên tố liên tiếp ~(p_{i}, p_{i+1})~ thỏa mãn ~l \leq p_i \leq p_{i+1} \leq r~.

Input

• Gồm một dòng duy nhất chứa hai số nguyên dương ~l~ và ~r~ ~(5 \leq l, r \leq 10^{12}; r - l \leq 10^{6})~.

Output

• In ra một số nguyên duy nhất là phần dư của ~S~ khi chia cho ~10^{9} + 7~.

Scoring

• Subtask ~1~ (~20\%~ số điểm): ~5 \leq l, r \leq 10^3~.
• Subtask ~2~ (~30\%~ số điểm): ~5 \leq l, r \leq 10^6~.
• Subtask ~3~ (~50\%~ số điểm): không có rằng buộc gì thêm.

Example

Input

5 11

Output

112

Input

100 113

Output

130420

Explanation

Ở ví dụ đầu tiên, với đoạn ~[l, r] = [5, 11]~ có các cặp nguyên tố liên tiếp: ~(5, 7), (7, 11)~:

• Với cặp ~(5, 7)~: số nhỏ nhất chia hết cho ~7~ và có đuôi là ~5~ là ~35~.
• Với cặp ~(7, 11)~: số nhỏ nhất chia hết cho ~11~ và có đuôi là ~7~ là ~77~.

Tổng giá trị ~f(i)~ tương ứng là ~35 + 77 = 112~.

Ở ví dụ thứ hai, với đoạn ~[l, r] = [100, 113]~ có các cặp: ~(101, 103), (103, 107), (107, 109), (109, 113)~.

• Với cặp ~(101, 103)~: số nhỏ nhất chia hết cho ~103~ và có đuôi là ~101~ là ~48101~.
• Với cặp ~(103, 107)~: số nhỏ nhất chia hết cho ~107~ và có đuôi là ~103~ là ~3103~.
• Với cặp ~(107, 109)~: số nhỏ nhất chia hết cho ~109~ và có đuôi là ~107~ là ~46107~.
• Với cặp ~(109, 113)~: số nhỏ nhất chia hết cho ~113~ và có đuôi là ~109~ là ~33109~.

Tổng giá trị ~f(i)~ tương ứng là ~48101 + 3103 + 46107 + 33109 = 130420~. **

Ban đầu, bạn có một mảng chỉ chứa duy nhất một phần tử là số ~0~. Đồng thời, bạn có một danh sách dự trữ gồm tất cả các số tự nhiên dương ~1, 2, 3, 4, 5, \ldots~ theo thứ tự tăng dần.

Bạn sẽ thực hiện ~q~ thao tác liên tiếp. Mỗi thao tác được mô tả bởi hai số nguyên ~p~ và ~k~, có ý nghĩa như sau:

• Nếu ~k > 0~: thực hiện thao tác insert(p, k) — lấy ~k~ số nhỏ nhất hiện còn trong danh sách dự trữ và chèn chúng ngay sau phần tử có giá trị bằng ~p~ trong mảng. Các số vừa chèn sẽ bị xóa khỏi danh sách dự trữ.
• Nếu ~k < 0~: thực hiện thao tác remove(p, |k|) — trong mảng hiện tại, tìm phần tử có giá trị bằng ~p~ và xóa |k| phần tử liền sau nó (nếu có). Các phần tử bị xóa không được hoàn lại vào danh sách dự trữ.

Sau mỗi thao tác, hãy in ra phần tử giữa của mảng hiện tại. Nếu mảng có độ dài ~n~, phần tử giữa là phần tử có chỉ số ~\lceil n / 2 \rceil~ (đánh số từ ~1~).

Input

• Dòng đầu tiên chứa số nguyên dương ~q~ ~(1 \leq q \leq 5 \times 10^{5})~ là số lượng thao tác.
• Mỗi trong ~q~ dòng tiếp theo chứa hai số nguyên ~p_i, k_i~ ~(1 \leq p_i \leq 2 \times 10^9~; ~|k_i| \leq 2 \times 10^9)~ mô tả thao tác thứ ~i~:
  • Nếu ~k_i > 0~: thực hiện thao tác insert(p_i, k_i)
  • Nếu ~k_i < 0~: thực hiện thao tác remove(p_i, |k_i|)
• Các thao tác đều hợp lệ (bảo đảm phần tử ~p_i~ tồn tại và không xóa vượt giới hạn). Tổng số phần tử được chèn từ danh sách dự trữ không vượt quá ~2 \times 10^9~.

Output

• Sau mỗi thao tác, in ra một số nguyên duy nhất — giá trị của phần tử giữa của mảng sau khi thao tác đó hoàn tất.

Scoring

• Subtask ~1~ (~30\%~ số điểm): ~q \leq 100~.
• Subtask ~2~ (~30\%~ số điểm): ~q \leq 10^4~.
• Subtask ~3~ (~40\%~ số điểm): không có rằng buộc gì thêm.

Example

Input

7
0 3
0 2
5 -2
4 1
0 -2
5 2
7 3

Output

1
5
4
6
5
7
9

Explanation

Khởi tạo mảng: ~[0]~.

• Thao tác ~1~: insert(0, 3) — chèn ~[1, 2, 3]~ sau ~0 \rightarrow [0, 1, 2, 3] \rightarrow~ phần tử giữa là ~1~.
• Thao tác ~2~: insert(0, 2) — chèn ~[4, 5]~ sau ~0 \rightarrow [0, 4, 5, 1, 2, 3] \rightarrow~ phần tử giữa là ~5~.
• Thao tác ~3~: remove(5, 2) — xóa ~[1, 2]~ sau ~5 \rightarrow [0, 4, 5, 3] \rightarrow~ phần tử giữa là ~4~.
• Thao tác ~4~: insert(4, 1) — chèn ~[6]~ sau ~4~ → ~[0, 4, 6, 5, 3] \rightarrow~ phần tử giữa là ~6~.
• Thao tác ~5~: remove(0, 2) — xóa ~[4, 6]~ sau ~0~ → ~[0, 5, 3] \rightarrow~ phần tử giữa là ~5~.
• Thao tác ~6~: insert(5, 2) — chèn ~[7, 8]~ sau ~5~ → ~[0, 5, 7, 8, 3] \rightarrow~ phần tử giữa là ~7~.
• Thao tác ~7~: insert(7, 3) — chèn ~[9, 10, 11]~ sau ~7 \rightarrow [0, 5, 7, 9, 10, 11, 8, 3] \rightarrow~ phần tử giữa là ~9~.

Việt Nam có ~n~ thành phố, được kết nối với nhau bởi ~m~ con đường hai chiều.

Mỗi con đường nối trực tiếp hai thành phố khác nhau. Hệ thống giao thông này được thiết kế sao cho bất kỳ hai thành phố nào cũng có thể đi đến nhau thông qua một số con đường — tức là mạng lưới này liên thông.

Một ngày nọ, một trận mưa lớn kéo dài nhiều giờ đã khiến chính phủ lo ngại rằng một số con đường có thể bị ngập nước. Chính phủ muốn đánh giá mức độ ảnh hưởng của việc ngập lụt bằng cách xem xét các tình huống sau:

Nếu một con đường bị ngập và hai thành phố mà nó kết nối cũng chìm trong nước, thì liệu các thành phố còn lại có còn đi lại được với nhau hay không?

Yêu cầu: Hãy xác định có bao nhiêu con đường mà nếu xóa bỏ con đường đó cùng hai thành phố mà nó nối, thì phần còn lại của mạng lưới không còn liên thông.

Input

• Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~m~ ~(4 \le n \le 10^5, n - 1 \le m \le 3 \times 10^5)~ là số lượng thành phố và số lượng con đường.
• ~m~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~a_i~ và ~b_i~ ~(1 \le a_i, b_i \le n, a_i \ne b_i)~ biểu diễn một con đường nối giữa hai thành phố ~a_i~ và ~b_i~.
• Đảm bảo không có con đường trùng hoặc tự nối một thành phố với chính nó.

Output

• In ra một số nguyên duy nhất — số lượng con đường có tính chất như mô tả.

Scoring

• Subtask ~1~ (~20\%~ số điểm): ~n \le 100~, ~m \le 300~.
• Subtask ~2~ (~20\%~ số điểm): ~n \le 1000~, ~m \le 3000~.
• Subtask ~3~ (~20\%~ số điểm): ~n \le 1000~.
• Subtask ~4~ (~20\%~ số điểm): ~m - n \le 20~.
• Subtask ~5~ (~20\%~ số điểm): Không có ràng buộc thêm.

Examples

Input

4 5
1 2
2 3
3 4
4 1
1 3

Output

1

Input

6 7
1 2
2 4
2 6
3 5
6 1
4 3
2 5

Output

4

Explanation

Ví dụ 1:

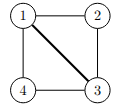
Chỉ có con đường ~(1, 3)~ có tính chất mà đề bài yêu cầu.

Khi hai thành phố ~1~ và ~3~ cùng bị ngập, mạng lưới còn lại chỉ gồm hai thành phố ~2~ và ~4~, không còn kết nối với nhau.

Ví dụ 2:

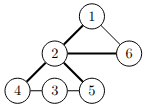
Các con đường có tính chất mà đề bài yêu cầu là ~(1, 2)~, ~(2, 4)~, ~(2, 6)~, ~(2, 5)~.

Nếu bất kỳ con đường nào trong số này và hai thành phố mà nó nối bị ngập, mạng lưới còn lại sẽ bị chia cắt.