Given an integer ~d~ ~(20 \le d \le 50)~ is a shortest side of a square. Draw a picture pinwheel as below.

Write a program that allows entering the dimension ~d~ ~(20 ≤ d ≤ 50)~, which is the length of the shortest straight segment in the picture. The longer side of the pinwheel has a size of ~2~ x ~d~, and the background square has a side length of ~6~ x ~d~. The center of the pinwheel coincides with the center of the square, and draw all the necessary black outlines of the figure.

Note

• You can use different colors to fill the background of the pinwheel and the square, but their borders must be in black..
• Do not use characters similar to the drawing.

Scoring

• The system will save the last submitted drawing and score it after the end of the exam.

Given a series of numbers with the following rules: ~1, 2, 6, 24, 120,...~

Calculate the sum of the first ~N~ terms.

Input Specification

• The first and only line of input contains an integer ~N~ ~(N \le 100)~.

Output Specification

• Output the the sum of the first ~N~ terms modulo ~10^9+7~.

Examples

Input

4

Output

33

Given an array of ~n~ integers ~a_1, a_2,…, a_n~. Find the second smallest and second largest number.

Input Specification

• The first line of input contains an integer ~n~ ~(1 \le n \le 100)~.
• Then ~n~ lines follow, the ~i~-th of which contains an integer ~a_i~ ~(|a_i| \le 10^5)~ - the ~i~-th element of array

Output Specification

• Output the second smallest and second largest number separated by a space.

Examples

Input

5
2
1
9
7
7

Output

2 7

A pyramid as shown on the right is created by natural numbers according to the following rules:

• The first line contains only ~1~ number ~1~.
• Line ~i~ includes consecutive natural numbers from ~1~ to ~i~ and then gradually decreasing to ~1~.

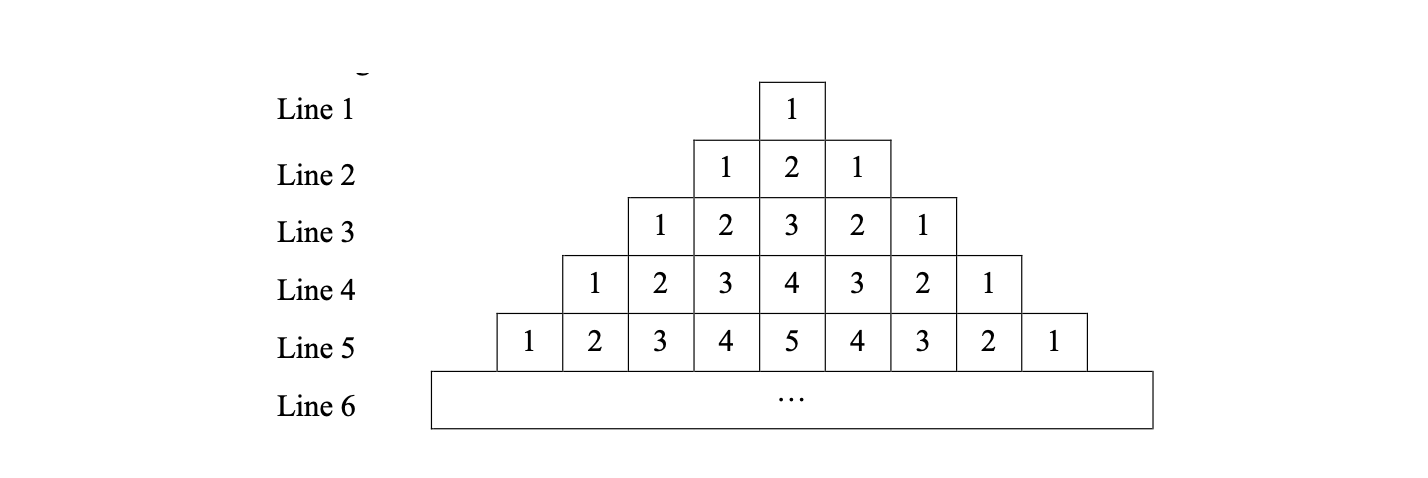
Your task is to calculate sum of the numbers of the pyramid from line ~1~ to line ~n~.

Input Specification

• The first and only line of input contains an integer ~n~ ~(1 \le n \le 10^9)~.

Output Specification

• Output the sum of the numbers of the pyramid from line ~1~ to line ~n~.

Examples

Input

5

Output

55

Constraints

For all subtasks:

• ~1 \le n \le 10^9~

Subtask 1 [40%]

• ~n \le 100~

Subtask 2 [40%]

• ~n \le 1000~

Subtask 3 [20%]

• No additional constraints. Output only the last ~3~ digits of the answer because the result can be large.

Given a positive integer ~X~. In one operation, you must replace ~X~ obtained by the sum of the digits of ~X~, and so on until ~X~ has only ~1~ digit left.

For example, ~X = 148~, replace ~X = 1 + 4 + 8 = 13~, then replace ~X = 13~ to ~X = 1 + 3 = 4~, then end.

Calculate the sum of the last digits of numbers from ~A~ to ~B~.

Input Specification

• The first line of input contains an integer ~A~ ~(1 \le A \le 10^9)~.
• The second line of input contains an integer ~B~ ~(A \le B \le 10^9)~.

Output Specification

• Output a number that is the sum of the last digits of numbers from ~A~ to ~B~.

Examples

Input

395
398

Output

20

Note

• Number ~395 → 3 + 9 + 5 = 17~; number ~17 → 1 + 7 = 8~
• Number ~396 → 3 + 9 + 6 = 18~; number ~18 → 1 + 8 = 9~
• Number ~397 → 3 + 9 + 7 = 19~; number ~19 → 1 + 9 = 10;~ number ~10 → 1 + 0 = 1~
• Number ~398 → 3 + 9 + 8 = 20~; number ~20 → 2 + 0 = 2~
• So we need to give the total ~8 + 9 + 1 + 2 = 20~

Constraints

For all subtasks:

• ~1 \le A \le B \le 10^9~

Subtask 1 [40%]

• ~1 \le A \le B \le 10^4~

Subtask 2 [60%]

• No additional constraints.