Cho một cây vô hướng gồm ~n~ đỉnh và số nguyên dương ~k~.

Đếm các cặp đỉnh ~(u,v)~ ~(u > v)~ sao cho khoảng cách của chúng trên cây bằng ~k~.

Input

• Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~k~ ~(1 \le k \le n \le 10^6)~.
• ~n-1~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên dương ~u_i,v_i~ ~(1 \le u_i,v_i \le n u_i \neq v_i;)~.

Output

• In ra một số nguyên không âm là kết quả bài toán.

Ràng buộc

• Có ~25\%~ số test thỏa mãn: ~k \le 50, n \le 1000~.
• Có ~25\%~ số test thỏa mãn: ~k \le 500, n \le 5 \times 10^4~.
• Có ~25\%~ số test thỏa mãn: ~n \le 10^5~.
• Có ~25\%~ số test thỏa mãn: ~n \le 10^6~.

Ví dụ

Input

5 2
1 2
2 3
3 4
2 5

Output

4

Kết hợp với IOI, thành phố Pattaya sẽ tổ chức cuộc đua: Olympic quốc tế về đua tốc độ (IOR) 2011.

Là nhà tổ chức, chúng ta phải tìm ra vòng đua tốt nhất nếu cuộc thi tốc độ này được tổ chức.

Ở vùng Pattaya - Chonburi, có ~N~ thành phố được nối với nhau bởi ~N - 1~ đường cao tốc. Mỗi đường cao tốc đều cho phép đi theo cả hai chiều và nối hai thành phố phân biệt với độ dài đo bởi kilomet là số nguyên. Ngoài ra, có đúng một đường đi giữa mỗi cặp thành phố bất kỳ. Nghĩa là, có đúng một cách đi từ một thành phố này tới một thành phố khác sao cho không đi qua thành phố nào quá một lần (đồ thị là cây).

IOR có quy tắc đặc biệt: đội nào vượt qua vòng đua dài đúng ~K~ kilomet, bắt đầu và kết thúc ở hai thành phố phân biệt, thì sẽ chiến thắng. Rõ ràng là không có đường cao tốc (và vì thế cũng không có thành phố) nào có thể được sử dụng nhiều hơn một lần trên vòng đua để ngăn ngừa ùn tắc. Vòng đua phải chứa một số ít nhất 1 thành phố.

Yêu cầu: Bạn hãy cho biết số lượng đường cao tốc nhỏ nhất trên vòng đua hợp quy tắc có độ dài đúng ~K~. Nếu không tìm được vòng đua như vậy, kết quả sẽ là ~-1~.

Input

Dòng đầu ghi hai số nguyên ~N, K~.

~N - 1~ dòng tiếp theo, mỗi dòng chứa ba số nguyên ~u, v, l~ - đường cao tốc nối thành phố ~u~ và ~v~, có độ dài ~l~.

Output

Một số nguyên duy nhất - là số lượng đường cao tốc ít nhất tạo thành vòng đua dài đúng ~K~, hoặc ~-1~ nếu không có.

Giới hạn

• ~1 \leq N \leq 2 \times 10^5~

• ~1 \leq K \leq 10^6~

• 1 \leq l \leq 10^6~

Sample Input 1

4 3
0 1 1
1 2 2
1 3 4

Sample Output 1

2

Thành có một cây gồm ~n~ đỉnh, được đánh số từ ~1~ đến ~n~. Mỗi đỉnh ~i~ có trọng số là ~a_i~.

Thành muốn tìm hiểu các vùng liên thông trong cây. Một vùng liên thông được định nghĩa là một tập các đỉnh sao cho giữa hai đỉnh bất kỳ trong tập này luôn tồn tại một đường đi chỉ gồm các đỉnh trong tập đó.

Với mỗi số nguyên ~k~ từ ~1~ đến ~n~, hãy xác định tổng trọng số lớn nhất của một vùng liên thông gồm đúng ~k~ đỉnh.

Input

Dòng đầu tiên chứa số nguyên ~n~ (~1 \leq n \leq 5000~) — số lượng đỉnh của cây.

Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \dots, a_n~ (~|a_i| \leq 10^4~) — trọng số của các đỉnh.

Mỗi dòng trong ~n-1~ dòng tiếp theo chứa hai số nguyên ~u~ và ~v~ (~1 \leq u, v \leq n~) — biểu diễn một cạnh nối đỉnh ~u~ và ~v~.

Output

In ra ~n~ dòng, dòng thứ ~k~ chứa một số nguyên là tổng trọng số lớn nhất của một vùng liên thông gồm đúng ~k~ đỉnh.

Sample Input 1

5
1 2 3 4 5
1 2
1 3
3 4
3 5

Sample Output 1

5
8
12
13
15

Giải thích

Với ~k = 1~: chọn đỉnh có trọng số lớn nhất là đỉnh 5 → ~5~

Với ~k = 2~: chọn đỉnh 5 và 3 → ~5 + 3 = 8~

Với ~k = 3~: chọn 3-4-5 → ~3 + 4 + 5 = 12~

Với ~k = 4~: chọn 1-3-4-5 → ~1 + 3 + 4 + 5 = 13~

Với ~k = 5~: toàn bộ cây → ~1 + 2 + 3 + 4 + 5 = 15~

Thành vẽ một cây (đồ thị vô hướng liên thông không có chu trình) với ~N~ nút được đánh số từ 1 đến ~N~ và muốn tô màu các nút của cây bằng màu đen hoặc trắng. Trên cây, hai nút có thể ghép đôi với nhau khi và chỉ khi chúng thỏa mãn các điều kiện sau:

• cả hai cùng được tô bởi màu trắng, và
• hoặc là có cạnh nối trực tiếp giữa chúng hoặc là có thể nối chúng bởi một đường đi đơn chỉ gồm toàn nút màu đen ngoại trừ hai nút đầu mút là màu trắng.

Yêu cầu: hãy giúp Thành tô màu các nút của cây bằng màu đen hoặc trắng sao cho số lượng cặp nút có thể ghép đôi với nhau là lớn nhất.

Input

Dòng đầu tiên chứa một số nguyên dương ~T~ (~T\leq 10~) là số lượng bộ test, mỗi bộ test chứa thông tin về một cây cần tô màu có cấu trúc như sau:

• Dòng thứ nhất chứa một số nguyên dương ~N~ (~N \leq 5000~) là số lượng nút của cây;
• Mỗi dòng trong số ~N-1~ dòng tiếp theo chứa hai số nguyên ~x~ ~y~ cách nhau bởi dấu cách cho biết có cạnh nối trực tiếp giữa hai nút ~x~ và ~y~.

Output

• Ghi ra ~T~ dòng, mỗi dòng một số nguyên là kết quả tìm được tương ứng với các bộ test trong dữ liệu vào.

Scoring

• Subtask ~1~: ~T=1~ và ~N\leq 15~
• Subtask ~2~: ~T=1~ và ~N\leq 20~
• Subtask ~3~: ~N\leq 500~ và mỗi cây trong dữ liệu vào có đúng 2 lá
• Subtask ~4~: ~N\leq 500~
• Subtask ~5~: Không có ràng buộc gì thêm

Sample Input 1

2
8
1 2
2 3
2 4
4 5
5 6
6 7
6 8
2
1 2

Sample Output 1

7
1

Explaination

Có 2 bộ test trong dữ liệu vào (T = 2).

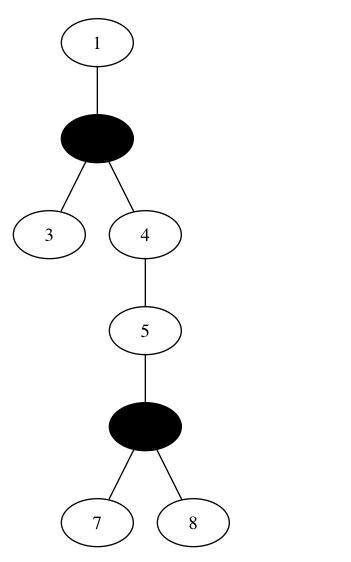
Đối với bộ test thứ nhất, cây có 8 nút và 7 cạnh, trong hình vẽ là cách tô màu cho số lượng cặp nút có thể ghép đôi là lớn nhất (7 cặp). Các cặp đó là: (1, 3), (1, 4), (3, 4), (4, 5), (5, 7) (5, 8), (7, 8).

Một ngân hàng có ~n~ chi nhánh, mỗi chi nhánh có một máy chủ, các máy chủ ở các chi nhánh được đánh số từ ~1~ đến ~n~. Nhằm bảo đảm việc truyền thông giữa các chi nhánh, ngân hàng đã thuê ~n-1~ kênh truyền tin trực tiếp từ một nhà máy cung cấp dịch vụ mạng để kết nối ~n~ máy chủ thành một mạng máy tính và bảo đảm từ máy chủ của một chi nhánh bất kì có thể truyền tin đến tất cả các máy chủ của các chi nhánh còn lại theo kênh truyền tin trực tiếp giữa chúng hoặc thông qua đường truyền đi qua một số máy chủ của các chi nhánh nào đó.

Trong thời gian tới, ngân hàng muốn lựa chọn ~k~ máy chủ trong ~n~ máy chủ để cài đặt phần mềm kiểm soát. Phần mềm khi hoạt động sẽ làm tăng lưu lượng truyền trên các kênh giữa ~k~ máy chủ này. Với mỗi phương án chọn ~k~ máy chủ để cài đặt phần mềm, trong số ~n-1~ kênh truyền tin, nhà cung cấp dịch vụ mạng đã xác định một số ít nhất các kênh đủ để kết nối ~k~ máy chủ này và khuyến cáo ngân hàng cần phải nâng cấp các kênh đó. Vì lí do kĩ thuật cũng như kinh phí, ngân hàng muốn lựa chọn ~k~ máy chủ để cài đặt phần mềm mà số lượng kênh ít nhất cần nâng cấp có giá trị nằm trong đoạn ~[a,b]~. Cụ thể, với mỗi cách chọn ~k~ máy chủ, gọi ~s~ là số kênh ít nhất cần chọn ra trong ~n-1~ kênh truyền tin nhằm đảo bảo liên thông giữa ~k~ máy chủ được chọn ngay cả khi các kênh còn lại bị đứt kết nối, ~s~ kênh này sẽ được khuyến cáo nâng cấp, khi đó, cách chọn ~k~ máy chủ thỏa mãn yêu cầu của ngân hàng nếu ~a \le s \le b~.

Yêu Cầu: Cho ~n-1~ kênh truyền tin và các giá trị ~k,a,b~ hãy đếm số lượng cách chọn ~k~ máy chủ để cài đặt phần mềm mà số lượng kênh ít nhất cần nâng cấp nằm trong đoạn ~[a,b]~.

Input

• Dòng đầu ghi bốn số nguyên dương ~n,k,a,b~ ~(k < n; 1 < a \le b < n)~.
• Dòng thứ ~i~ trong số ~n-1~ dòng tiếp theo chứa hai số nguyên dương ~u_i~ và ~v_i~ cho biết kênh truyền tin trực tiếp giữa hai máy chủ ~u_i,v_i~.

Constraints

• ~1 \le n \le 10^5~

Subtask

• ~20\%~ số test: ~n \le 100~ và ~k = 2~.
• ~30\%~ số test: ~n \le 100~ và ~k = 3~.
• ~20\%~ số test: ~n \le 100~ và ~k = 4~.
• ~20\%~ số test: ~n \le 1000~ và ~k = 3~.
• ~10\%~ số test: ~n \le 1000~ và ~k = 4~.

Output

• Ghi một số nguyên duy nhất là số cách chọn ~k~ máy chủ để cài đặt phần mềm thỏa mãn yêu cầu của ngân hàng.

Sample Input 1

6 3 2 3
1 2
2 3
3 4
4 5
3 6

Sample Output 1

14

Explanation 1

Có ~5~ cách với số đường truyền cần nâng cấp là ~2~: ~(1,2,3); (2,3,4); (2,3,6); (3,4,5); (3,4,6)~

Có ~9~ cách với số đường truyền cần nâng cấp là ~3~.

Cho một cây gồm ~n~ đỉnh và số nguyên dương ~k~.

Bạn cần xóa một vài cạnh ở trên cây. Sau đó, cây sẽ trở thành một "rừng" với nhiều cây con, tập cạnh bạn xóa được gọi là tốt nếu như tất cả các cây con đều có đường kính không lớn hơn ~k~.

Hãy đếm số tập cạnh thỏa mãn.

Input

• Dòng đầu gồm hai số nguyên dương ~n,k~.
• ~n-1~ dòng tiếp theo, mỗi dòng gồm hai số nguyên ~u~, ~v~ miêu tả cạnh của cây.

Output

• In ra số tập cạnh thỏa mãn theo module ~998244353~.

Constraints

• ~1 \le n,k \le 5 \times 10^3~.

Subtask

• ~30\%~ số điểm có ~n \le 20~.
• ~30\%~ số điểm có ~n \le 100~.
• ~40\%~ số điểm có ~n \le 5000~

Sample Input 1

6 2
1 3
2 4
3 2
1 5
4 6

Sample Output 1

24

Cho một cây gồm ~N~ đỉnh. Cạnh thứ ~i~ trên cây có trọng số ~w_i~. Độ dài đường đi giữa hai đỉnh ~u~ và ~v~ được định nghĩa là tổng các cạnh nằm trên đường đi phải qua ít cạnh nhất từ ~u~ tới ~v~. Chọn ~K~ đỉnh lá sao cho tổng độ dài đường đi giữa mọi cặp đỉnh trong ~K~ đỉnh đã chọn là nhỏ nhất có thể.

Input

• Dòng đầu tiên chứa hai số nguyên dương ~N~ và ~K~ ~(1≤K≤N)~.
• ~N-1~ dòng tiếp theo, mỗi dòng chứa thông tin về một cạnh của cây từ nút ~u_i~ đến ~v_i~ với trọng số ~w_i~ ~(1≤w_i≤10^5)~.

Output

• Gồm một số nguyên duy nhất là tổng khoảng cách nhỏ nhất trong cách chọn K nút lá tốt nhất.

Scoring

• Sub1: ~1 ≤ N ≤ 20~;
• Sub2: ~1 ≤ N ≤10^5, K=2~;
• Sub3: ~1 ≤ N ≤2000, K=3~;
• Sub4: ~1 ≤ N ≤10^5, K≤100~.

Example

Input

4 2
1 2 2
1 3 3
1 4 4

Output

5

Input

4 3
1 2 2
1 3 3
1 4 4

Output

18

https://oj.vnoi.info/problem/kingdom

Thời xưa có ~N~ đế chế tọa lạc trên một vùng đất xa xăm nọ, chiến đấu tranh giành lẫn nhau. Vua của đế chế hùng mạnh nhất quyết định chinh phục các đế chế khác để tìm kiếm nguồn dầu hòa! Kho tàng của đế chế này bị hạn chế vì tiền đã được đổ vào chiến dịch từ trước, nên chỉ còn lại một lượng tiền là ~M~.

Các đế chế được đánh số từ ~1~ đến ~N~. Đế chế ~1~ là đế chế hùng mạnh nhất. Các đế chế được nối với nhau bởi các đường nối hai chiều, trong đó chỉ có đúng một đường đi giữa hai đế chế bất kỳ.

Nhà vua thuê bạn để hoạch định chiến lược cho ông. Các điệp viên của nhà vua cho bạn hai thông số đối với mỗi đế chế ~i~ (~i > 1~):

~V_i~ = giá trị của nguồn dầu hòa của nước ~i~.

~C_i~ = chi phí để chinh phục nước ~i~.

Một đế chế chỉ có thể bị chinh phục khi nó kề với đế chế ~1~ hoặc đế chế ~1~ đã chinh phục một đế chế kề với nó (nối với nó qua một con đường).

Bạn hãy hoạch định một chiến lược chinh phục các đế chế khác sao cho tổng giá trị thu được từ nguồn dầu hòa là lớn nhất, nhưng không được vượt quá giới hạn của kho tàng!

Input

• Dòng đầu tiên chứa hai số nguyên ~N~ (~1 \leq N \leq 100~) và ~M~ (~0 \leq M \leq 2000~).

• Dòng thứ hai chứa ~N - 1~ số nguyên ~V_2, V_3, \dots, V_N~ (~1 \leq V_i \leq 100~).

• Dòng thứ ba chứa ~N - 1~ số nguyên ~C_2, C_3, \dots, C_N~ (~0 \leq C_i \leq 30~).

• Mỗi dòng trong ~N - 1~ dòng tiếp theo chứa hai số nguyên ~u, v~ — thể hiện một đường nối giữa hai đế chế.

Output

• Một số nguyên duy nhất - là tổng giá trị lớn nhất từ nguồn dầu hòa mà đế chế hùng mạnh nhất có thể thu được bằng việc chinh phục các đế chế khác.

Sample Input 1

10 3
10 10 10 9 5 8 8 7 10
0 0 0 0 0 3 2 2 0
1 2
1 3
1 4
2 5
3 6
4 7
5 8
6 9
8 10

Sample Output 1

62

Sample Input 2

3 1
1 1
1 0
1 2
2 3

Sample Output 2

2