khớp cầu
Cầu
Nộp bàiPoint: 100
Trong một thành phố có ~n~ nút giao thông và ~m~ đường hai chiều nối trực tiếp các cặp nút giao thông đó. Một đường giao thông giữa ~u~ và ~v~ được gọi là cầu nếu khi bỏ cạnh nối này đi ta không thể tìm được đường đi từ ~u~ tới ~v~.
Cho biết sơ đồ giao thông của thành phố, hãy xác định các cầu.
Input
Dòng ~1~: Ghi hai số nguyên dương ~n, m~ ~(n, m≤10^5)~.
~m~ dòng tiếp theo: mỗi dòng ghi hai số nguyên dương ~u, v~ biểu diễn đường đi từ ~u~ tới ~v~.
Output
Dòng ~1~: Ghi số ~k~ – số cầu.
~k~ dòng tiếp theo: mỗi dòng ghi ~2~ số nguyên biểu diễn một cầu. Mỗi cạnh đưa ra đỉnh nhỏ trước, lớn sau, và các cạnh đưa ra theo tăng dần theo thứ tự từ điển.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~50~ | ~n,q \le 1000~ |
| ~2~ | ~50~ | ~n,q \le 10^5~ |
Sample Input 1
13 14
1 3
3 6
6 4
4 1
4 2
2 5
5 7
7 4
6 9
9 8
8 4
8 10
11 12
5 12
Sample Output 1
3
5 12
8 10
11 12
Sample Explanation
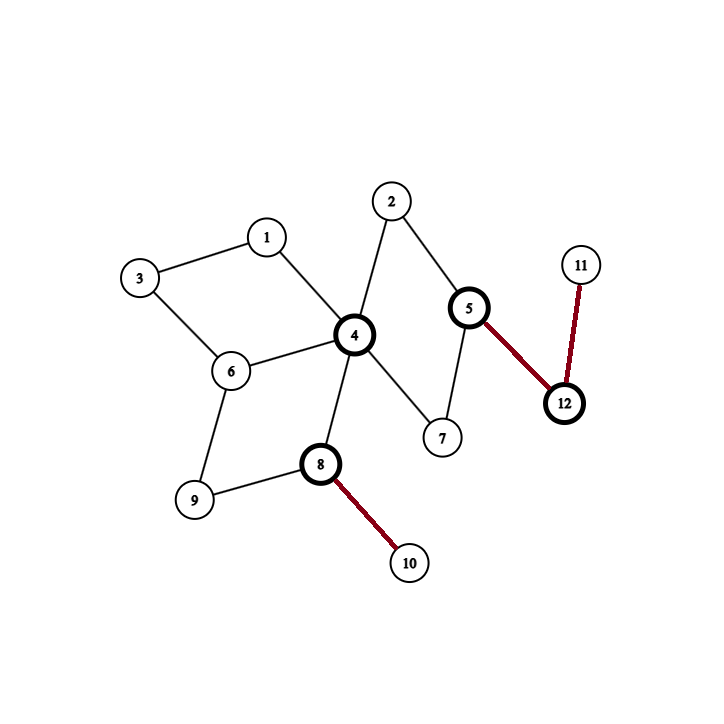
Chia phe
Nộp bàiPoint: 100
Trong một thành phố có ~n~ nút giao thông và ~m~ đường hai chiều nối trực tiếp các cặp nút giao thông đó. Mỗi nút trong thành phố chứa một tổ chức buôn yutam, một loại chất gây nghiện nhưng rất tốt cho tinh thần. Những tổ chức này đang muốn chia thành các phe phái khác nhau sao cho:
- Mỗi nhóm chứa nhiều tổ chức nhất có thể.
- Khi một đường đi bất kì bị cảnh sát lập chốt, mỗi tổ chức trong nhóm vẫn có thể đi đến một tổ chức bất kì khác trong nhóm bằng những con đường còn lại.
Hãy giúp các tổ chức này chia nhóm nhé.
Input
Dòng ~1~: Ghi hai số nguyên dương ~n, m~ ~(n, m≤10^5)~.
~m~ dòng tiếp theo: mỗi dòng ghi hai số nguyên dương ~u, v~ biểu diễn đường đi từ ~u~ tới ~v~.
Output
Dòng ~1~: Ghi số ~k~ – số nhóm.
~k~ dòng tiếp theo: số đầu là số ~l~ - số lượng tổ chức trong nhóm, theo sau là ~l~ số chứa chỉ số của các tổ chức trong nhóm đó.
Các chỉ số của các tổ chức trong một nhóm được đưa ra theo thứ tự tăng dần. Các nhóm được đưa ra theo số lượng tổ chức từ bé đến lớn, các nhóm có số lượng bằng nhau được đưa ra theo thứ tự từ điển.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~50~ | ~n,q \le 1000~ |
| ~2~ | ~50~ | ~n,q \le 10^5~ |
Sample Input 1
13 14
1 3
3 6
6 4
4 1
4 2
2 5
5 7
7 4
6 9
9 8
8 4
8 10
11 12
5 12
Sample Output 1
5
1 10
1 11
1 12
1 13
9 1 2 3 4 5 6 7 8 9
Sample Explanation

Đường truyền quan trọng
Nộp bàiPoint: 100
Cho một mạng gồm tập hợp các nút và tập các đường truyền hai chiều nối giữa các cặp mạng. Người ta biết rằng mạng này thông suốt, tức là mọi cặp nút trong mạng đều có thể truyền tin cho nhau. Một số nút trong mạng cung cấp dịch vụ ~A~ còn một số nút khác cung cấp dịch vụ ~B~ cho tất cả các nút (kể cả nó). Có thể có một nút cung cấp cả hai dịch vụ.
Nếu một đường truyền trực tiếp bị hỏng có thể làm cho một số nút trong mạng không thể sử dụng một trong hai dịch vụ. Các đường truyền như vậy được gọi là các đường truyền quan trọng.
Bạn hãy viết chương trình xác định số đường truyền quan trọng trong mạng.
Input
Dòng đầu tiên ghi ~4~ số ~N, M, K~ và ~L~. Trong đó ~N~ ~(1 ≤ N ≤ 10^5)~ là số nút trong mạng, ~M~ ~(1 ≤ M ≤ 10^5)~ là số đường truyền trực tiếp trong mạng, ~K~ ~(1 ≤ K ≤ N)~ là số nút cung cấp dịch vụ ~A~ và ~L~ ~(1 ≤ L ≤ N)~ là số nút cung cấp dịch vụ ~B~. Các nút được đánh số từ ~1~ đến ~N~.
Dòng thứ hai ghi ~K~ số là số hiệu các nút cung cấp dịch vụ ~A~.
Dòng thứ ba ghi ~L~ số là số hiệu các nút cung cấp dịch vụ ~B~.
Mỗi dòng trong số ~M~ dòng tiếp theo ghi hai số ~u, v~ ~(1 ≤ u, \; v ≤ N, u ≠ v)~ thể hiện một đường truyền trực tiếp nối nút ~u~ và nút ~v~.
Output
- Một số nguyên thể hiện số lượng đường truyền quan trọng trong mạng.
Sample Input 1
9 10 3 4
2 4 5
4 9 8 3
1 2
4 1
2 3
4 2
1 5
5 6
6 7
6 8
7 9
8 7
Sample Output 1
3
Khớp
Nộp bàiPoint: 100
Trong một thành phố có ~n~ nút giao thông và ~m~ đường hai chiều nối trực tiếp các cặp nút giao thông đó. Một nút giao thông ~c~ được gọi là khớp nếu tồn tại hai nút giao thông ~a~ và ~b~ ~(a, b, c~ đôi một khác nhau~)~ sao cho nếu nút ~c~ bị tắc thì không có cách nào đi từ ~a~ sang ~b~. Hay nói cách khác, mọi đường đi từ ~a~ tới ~b~ chắc chắn phải qua ~c~.
Cho biết sơ đồ giao thông của thành phố, hãy xác định các khớp.
Input
Dòng ~1~: Ghi hai số nguyên dương ~n, m~ ~(n, m≤10^5)~.
~m~ dòng tiếp theo: mỗi dòng ghi hai số nguyên dương ~u, v~ biểu diễn đường đi từ ~u~ tới ~v~.
Output
Dòng ~1~: Ghi số khớp.
Dòng ~2~: Ghi chỉ số của các khớp, các chỉ số này phải liệt kê đôi một khác nhau theo thứ tự tăng dần.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~50~ | ~n,q \le 1000~ |
| ~2~ | ~50~ | ~n,q \le 10^5~ |
Sample Input 1
13 14
1 3
3 6
6 4
4 1
4 2
2 5
5 7
7 4
6 9
9 8
8 4
8 10
11 12
5 12
Sample Output 1
4
4 5 8 12
Sample Explanation

Nút trung tâm
Nộp bàiPoint: 100
Trong một thành phố có ~n~ nút giao thông và ~m~ đường hai chiều nối trực tiếp các cặp nút giao thông đó. Nút ~u~ là nút trung tâm khi xóa nút đó và tất cả các đường đi có một trong hai đầu mút là ~u~ thì đồ thị sẽ tách thành nhiều thành phần liên thông nhất.
Cho biết sơ đồ giao thông của thành phố, hãy xác định các nút trung tâm.
Input
Dòng ~1~: Ghi hai số nguyên dương ~n, m~ ~(n, m≤10^5)~.
~m~ dòng tiếp theo: mỗi dòng ghi hai số nguyên dương ~u, v~ biểu diễn đường đi từ ~u~ tới ~v~.
Output
Dòng ~1~: Ghi số nút trung tâm.
Dòng ~2~: Ghi chỉ số của các nút trung tâm, các chỉ số này phải liệt kê đôi một khác nhau theo thứ tự tăng dần.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~50~ | ~n,q \le 1000~ |
| ~2~ | ~50~ | ~n,q \le 10^5~ |
Sample Input 1
13 14
1 3
3 6
6 4
4 1
4 2
2 5
5 7
7 4
6 9
9 8
8 4
8 10
11 12
5 12
Sample Output 1
4
4 5 8 12
Sample Explanation

Chốt
Nộp bàiPoint: 100
Trong một thành phố có ~n~ nút giao thông và ~m~ đường hai chiều nối trực tiếp các cặp nút giao thông đó. Thành phố này tạo thành một đồ thị liên thông. Ở mỗi nút giao thông có một tổ chức buôn yutam. Vào sáng mỗi ngày, các tổ chức thường vận chuyển yutam cho tất cả các tổ chức khác qua các con đường của thành phố. Vậy nên có tổng cộng là ~n \times (n - 1)~ cuộc vận chuyển diễn ra mỗi sáng.
Tuy nhiên dạo này công an hay lập chốt ở một số nút giao thông để chặn các cuộc vận chuyển. Không có cuộc vận chuyển nào có thể đi qua một nút có chốt. Hãy giúp các tổ chức biết khi mỗi thành phố ~i~ bị cấm thì sẽ có bao nhiêu cuộc vận chuyển không thực hiện được.
Input
Dòng ~1~: Ghi hai số nguyên dương ~n, m~ ~(n, m≤10^5)~.
~m~ dòng tiếp theo: mỗi dòng ghi hai số nguyên dương ~u, v~ biểu diễn đường đi từ ~u~ tới ~v~.
Output
Dòng ~1~: Chứa ~n~ số, số thứ ~i~ là số cuộc vận chuyển không thực hiện được khi nút giao thông ~i~ có chốt.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~30~ | ~n,q \le 100~ |
| ~2~ | ~30~ | ~n,q \le 1000~ |
| ~3~ | ~40~ | ~n,q \le 10^5~ |
Sample Input 1
12 14
1 3
3 6
6 4
4 1
4 2
2 5
5 7
7 4
6 9
9 8
8 4
8 10
11 12
5 12
Sample Output 1
24 24 24 94 64 24 24 46 24 24 24 46 24
Sample Explanation
