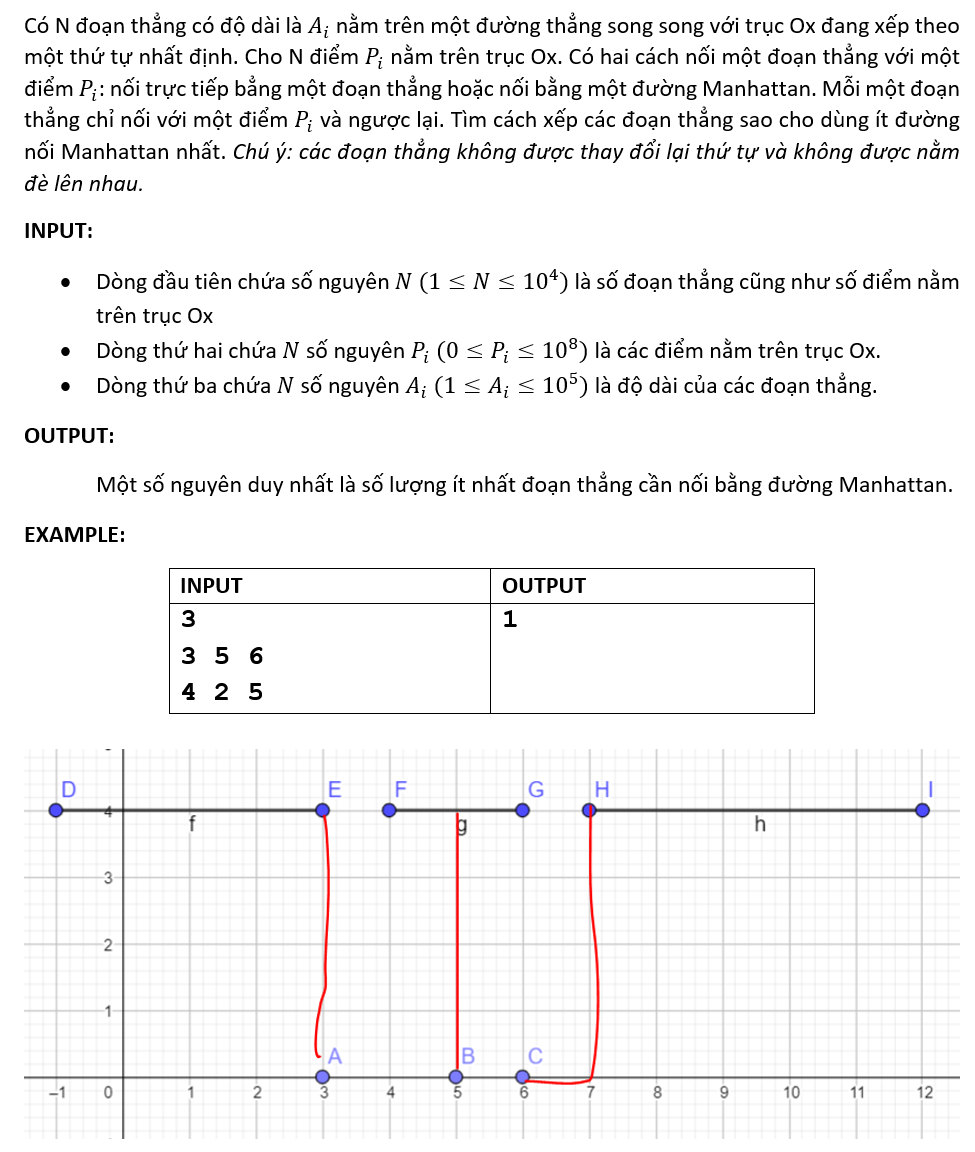
Cho hai đường thẳng ~d_1: y = y_1~ và ~d_2: y = y_2~. Cho ~n~ điểm phân biệt trên đường thẳng ~d_1~ (có hoành độ ~x_{11}~, ~x_{12}~, ..., ~x_{1n}~) và ~m~ điểm phân biệt trên đường thẳng ~d_2~ (có hoành độ ~x_{21}~, ~x_{22}~, ..., ~x_{2m}~). Hãy tìm khoảng cách Manhattan nhỏ nhất giữa hai điểm ~(A, B)~ với ~A \in d_1~ và ~B \in d_2~ và đếm số cặp điểm ~(A, B)~ phân biệt có khoảng cách Manhattan nhỏ nhất.

Input

• Dòng đầu tiên chứa hai số nguyên dương ~n~, ~m~ (~n, m \le 10^6~)
• Dòng thứ hai chứa hai số nguyên ~y_1~, ~y_2~ (~-10^9 < y_1, y_2 < 10^9~)
• Dòng thứ ba chứa ~n~ số nguyên phân biệt ~x_{11}~, ~x_{12}~, ..., ~x_{1n}~ (~-10^9 < x_{1i} < 10^9~)
• Dòng thứ tư chứa ~m~ số nguyên phân biệt ~x_{21}~, ~x_{22}~, ..., ~x_{2m}~ (~-10^9 < x_{2i} < 10^9~)

Output

• Một dòng duy nhất gồm hai số nguyên: khoảng cách Manhattan ngắn nhất và số cặp có khoảng cách như vậy.

Sample Test

Input

3 4
1 -2
3 0 6
5 -2 4 2

Output

4 3

Giải thích

Có ~3~ cặp điểm ~(A, T)~, ~(A, Z)~, ~(C, X)~

Cho ba số nguyên dương ~a,b,c~. Tìm số lớn thứ hai trong ba số đó. Biết số lớn thứ hai là số lớn hơn đúng một số trong hai số còn lại.

Input:

Gồm ba dòng, mỗi dòng chứa một số nguyên dương lần lượt là ba số ~a,b,c~ ~(a,b,c≤10^9)~.

Output:

Một số nguyên duy nhất là số lớn thứ hai trong ba số đã cho. Nếu không có số thoả mãn thì in ra ~-1~.

Sample Test 1

Input:

3
9
5

Output

5

Sample Test 2

Input:

6
6
6

Output

-1

Cho một số nguyên dương ~N~. Đếm xem có bao nhiêu số nguyên không âm nhỏ hơn ~N~ và có tận cùng là chữ số ~K~.

Input:

• Dòng đầu tiên chứa số nguyên dương ~N~ ~(N≤10^9)~.
• Dòng thứ hai chứa số nguyên ~K~ ~(0≤K≤9)~.

Output:

Một số nguyên duy nhất là số lượng số thoả mãn yêu cầu đề bài.

Ràng buộc

• Có ~70\%~ số test ứng với ~70\%~ số điểm của bài thoả mãn: ~N≤10^6~;
• ~30\%~ số test còn lại ứng với ~30\%~ số điểm của bài không có ràng buộc gì thêm.

Sample Test

Input:

68
3

Output

7

Giải thích

Các số thoả mãn là: ~3,13,23,33,43,53,63~.

Cho một dãy số nguyên ~A~ gồm ~N~ phần tử ~A_1,A_2,…,A_N~. In ra độ dài của dãy con liên tiếp đan dấu dài nhất. (Đan dấu là không có hai phần tử nào cạnh nhau mà có cùng dấu)

Input:

• Dòng đầu tiên gồm một số nguyên dương ~N~ ~(N≤10^5)~ là số lượng phần tử của dãy ~A~.
• Dòng thứ hai gồm ~N~ số nguyên ~A_1,A_2,…,A_N~ mô tả dãy ~A~ ~(0<|A_i|≤10^9)~.

Output:

Ghi ra một số nguyên duy nhất là độ dài của dãy con liên tiếp đan dấu dài nhất.

Ràng buộc

• Có ~60\%~ số test ứng với ~60\%~ số điểm có ~N≤10^3~;
• ~40\%~ số test còn lại ứng với ~40\%~ số điểm không có ràng buộc gì thêm.

Sample Test 1

Input:

9
1 3 -1 3 -2 4 -5 -6 7

Output

6

Giải thích

Dãy đan dấu: 3 -1 3 -2 4 -5

Sample Test 2

Input:

9
1 3 -1 3 -2 4 -5 6 7

Output

7

Giải thích

Dãy đan dấu 3 -1 3 -2 4 -5 6

Cho hai xâu kí tự ~X,Y~ gồm các kí tự chữ thường. Kiểm tra xem hai xâu có phải là anagram của nhau hay ko? Hai xâu là anagram của nhau nếu hoán vị của xâu này sẽ là xâu kia.

Input

Gồm hai dòng, mỗi dòng gồm một xâu kí tự (có độ dài không quá ~10^5~ kí tự).

Output

Nếu hai xâu là anagram của nhau thì ghi ra YES, ngược lại thì ghi NO.

Sample Test 1

Input:

dear
read

Output

YES

Sample Test 2

Input:

dead
dae

Output

NO

Cho một dãy số ~A~ gồm ~N~ phần tử ~A_1,A_2,…,A_N~. Một dãy con liên tiếp từ ~L~ đến ~R~ của dãy số ~A~ là các phần tử ~A_L,A_{L+1},…,A_{R-1},A_R~ ~(1≤L≤R≤N)~. Cho một số nguyên dương ~T~, hãy đếm xem có bao dãy con của ~A~ có tổng các phần tử không quá ~T~.

Input:

• Dòng đầu tiên gồm hai số nguyên dương ~N~ và ~T~ là số lượng phần tử của dãy số ~A~ và số ~T~ cho trước ~(N≤10^6; T≤10^9)~;
• Dòng thứ hai gồm ~N~ số nguyên dương ~A_i~ mô tả các phần tử của dãy số ~A~ ~(1≤i≤N; A_i≤10^9)~.

Output:

Một số nguyên duy nhất là số lượng dãy con thoả mãn yêu cầu đề bài.

Ràng buộc:

• Có 50% số test tương ứng với 50% số điểm có ~N≤100~;
• Có 30% số test khác tương ứng với 30% số điểm có ~N≤5000~;
• 20% số test còn lại tương ứng với 30% số điểm không có ràng buộc gì thêm.

Sample Test 1

Input:

6 8
8 3 2 1 6 9

Output

9

Giải thích

Các dãy con thoả mãn: ~\{8\},\{3\},\{2\},\{1\},\{6\},\{3,2\},\{2,1\},\{1,6\},\{3,2,1\}~

Cho hai số nguyên dương ~L~ và ~R~.

Tìm số nguyên dương ~M~ bé nhất ~(L≤M<R)~ để chênh lệch giữa tổng các số nguyên liên tiếp từ ~L~ đến ~M~ và tổng các số nguyên liên tiếp từ ~M+1~ đến ~R~ là nhỏ nhất.</p>

Input

Gồm hai số nguyên dương ~L~ và ~R~ ~(L<R≤10^9)~.</p>

Output

Gồm một số nguyên duy nhất là số ~M~ thoả mãn.

Ràng buộc:

• Có ~60\%~ số test: ~L<R≤10^3~;</li>
• Có ~40\%~ số test còn lại: ~L<R≤10^9~.</li>

Sample Test

Input:

2 7

Output

5

Giải thích

Tổng từ ~2~ đến ~5~ là: ~14~.

Tổng từ ~6~ đến ~7~ là: ~13~

Chênh lệch là: ~1~

Số nguyên tố là một số tự nhiên chỉ gồm hai ước dương là ~1~ và chính nó. Nhiệm vụ của bạn là: Hãy đếm số lượng số nguyên tố nằm trong phạm vi từ ~L~ đến ~R~.

Input

• Dòng đầu tiên chứa số ~q~ ~(1 ≤ q ≤ 10^5)~ – số lượng truy vấn.
• ~q~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~L~ và ~R~ ~(1 ≤ L ≤ R ≤ 10^5)~

Output

Gồm ~q~ dòng, mỗi dòng tương ứng là số lượng số nguyên tố thuộc đoạn ~L~ đến ~R~ tương ứng với mô tả của đầu vào.

Sample Test

Input:

1
1 10

Output

4

NOTE: Nhầm test ví dụ:

INPUT
6 2
2
4
5
2
9
1

OUTPUT
11

Nông dân John (FJ) có ~N~ con bò đang đứng trên một hàng, mỗi con đứng ở một vị trí khác nhau trên trục số. Chúng đang luyện tập ném trái bóng chày vòng vòng để chuẩn bị cho một trận thi đấu quan trọng với những con bò láng giềng. Khi FJ theo dõi, ông ta nhận ra một nhóm có ba con bò ~(X,Y,Z)~ hoàn thành hai cú ném. Con bò ~X~ ném trái bóng cho con bò ~Y~ ở bên phải cô ta, và con bò ~Y~ ném trái bóng cho con bò ~Z~ ở bên phải cô ta. FJ để ý rằng lần ném thứ hai có độ dài không quá hai lần so với lần ném đầu tiên. Hãy giúp FJ đếm xem có bao nhiêu bộ ba các con bò ~(X,Y,Z)~ mà FJ có thể theo dõi.

Input

• Dòng ~1~: Số lượng các con bò là ~N~ ~(3 <= N <=1000)~.
• Dòng ~2..1+N~: Mỗi dòng chứ một số tự nhiên là vị trí của một con bò (các số tự nhiên nằm trong khoảng ~0..10^8~).

Output

In ra Số lượng bộ ba con bò ~(X,Y,Z)~, trong đó con bò ~Y~ nằm bên phải con bò ~X~, con bò ~Z~ nằm bên phải con bò ~Y~, và khoảng cách giữa ~Y~ và ~Z~ nằm giữa ~XY~ và ~2XY~ (bao gồm cả giá trị này), trong đó ~XY~ là khoảng cách của ~X~ đến ~Y~.

Sample Test

Input:

5 
3 
1 
10 
7 
4 

Output

4