Cho biểu thức như sau:

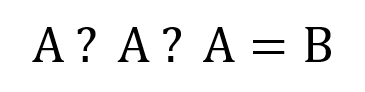
Hãy điền phép tính +, -, * vào ? để được biểu thức đúng.

Dữ liệu vào từ tệp văn bản: dienpheptinh.inp

• Dòng đầu tiên chứa số nguyên dương ~A~.
• Dòng đầu tiên chứa số nguyên dương ~B~.
• Dữ liệu đầu vào luôn đảm bảo có cách điền dấu phù hợp.

Kết quả ghi ra tệp văn bản: dienpheptinh.out

• In ra hai kí tự theo thứ tự là dấu của phép tính tương ứng. Có thể có nhiều cách điền, chỉ cần in ra cách điền đúng bất kì. Mỗi kí tự in trên một dòng (dòng đầu tiên là phép tính ở dấu hỏi đầu tiên, dòng thứ hai là phép tính ở dấu hỏi thứ hai).

Chú ý: dấu nhân là kí tự sao (*)

Ràng buộc

• Có ~60\%~ số test thỏa mãn: ~A, B \le 10^3~;
• Có ~20\%~ số test thỏa mãn: ~A, B \le 10^9~;
• Có ~20\%~ số test thỏa mãn: ~A, B \le 10^{18}~;

Ví dụ

Input

3
6

Output

*
-

Giải thích

~3*3-3=6~

Cho dãy số có quy luật như sau: ~1,2,2,3,3,3,4,4,4,4,5,5,…~ Cho một số tự nhiên ~N~, hãy tìm số thứ ~N~ của dãy số trên (các số được đánh thứ tự từ ~1~).

Input

• Gồm một số nguyên dương ~N~ ~(N ≤ 10^{15})~.

Output

• In ra kết quả của bài toán.

Subtasks

• Subtask 1 (~60\%~ số điểm): ~N ≤ 10^{6}~;
• Subtask 2 (~20\%~ số điểm): ~N ≤ 10^{10}~;
• Subtask 3 (~20\%~ số điểm): Không có ràng buộc gì thêm.

Sample Test

Input

5

Output

3

Cho một xâu ~S~ gồm các kí tự số. Hãy đếm xem có bao nhiêu xâu con chia hết cho ~4~ (xâu con có thể bắt đầu bằng ~0~).

Input:

Xâu ~S~ có độ dài không quá ~10^6~.

Output:

In ra kết quả của bài toán.

Scoring

• Subtask 1 [60%]: Xâu ~S~ có độ dài không quá ~100~.
• Subtask 2 [40%]: Không có ràng buộc gì thêm.

Examples

Input1

08

Output1

3

Giải thích

~0, 8, 08~

Input2

13085

Output2

5

Châu và Huy là đôi bạn thân. Vì yêu âm nhạc nên họ gửi cho nhau lyrics của các bài hát. Cụ thể đó là những xâu ~S~ độ dài ~N~ và chỉ gồm các kí tự từ ~a~ đến ~z~. Để làm cho những xâu này trở nên hay hơn, Huy đã đưa cho Châu một số nguyên dương ~K~ và nhờ thực hiện những thao tác sau. (Lưu ý mỗi thao tác bắt buộc phải làm một lần duy nhất):

• Tạo ra xâu ~T~ từ xâu ~S~ đã cho bằng cách viết ~K~ lần liên tiếp xâu ~S~ liên kề nhau. (Ví dụ ~K = 2~ và xâu ~S~ là ~hello~ thì khi viết sẽ cho xâu ~T~ là ~hellohello~).
• Chọn một chữ cái ở vị trí bất kì trong xâu ~T~, giả sử là vị trí ~i~. Biến đổi tất cả các chữ cái trong xâu ~T~ giống với chữ cái ở vị trí ~i~ thành chữ cái ở vị trí ~i-1~ hoặc chữ cái ở vị trí ~i+1~ (Tất nhiên nếu ở vị trí đầu tiên sẽ không có ~i-1~ và vị trí cuối cùng sẽ không có ~i+1~ để mà biến). Gọi ~X~ là số lần xuất hiện của chữ cái xuất hiện nhiều nhất trong xâu vừa tạo. Phải đảm bảo thao tác biến đổi vừa rồi tạo ra ~X~ lớn nhất.

Yêu cầu:

• Cho xâu ~S~ độ dài ~N~ và số ~K~. Tạo ra xâu ~T~ mới bằng viết liền xâu ~S~ cạnh nhau ~K~ lần. Sau đó thực hiện thao tác như đã miêu tả trong đề sao cho số lần xuất hiện của chữ cái xuất hiện nhiều nhất là lớn nhất và cho biết số lần xuất hiện là bao nhiêu.

Dữ liệu vào từ tệp văn bản: amnhac.inp

• Dòng đầu tiên là 2 số nguyên dương ~N~ và ~K~. ~(N \le 10^6, K \le 10^9)~
• Dòng thứ hai là xâu ~S~ chỉ gồm các kí tự từ ~a~ đến ~z~.

Kết quả ghi ra tệp văn bản: amnhac.out

• In ra một số nguyên duy nhất là số lần xuất hiện của chữ cái xuất hiện nhiều nhất sau các thao tác đã nêu trong đề.

Ràng buộc:

• Có ~20\%~ số điểm với ~N * K \le 10^3~
• Có ~30\%~ số điểm với ~K = 1~.
• ~50\%~ số điểm còn lại không có ràng buộc gì thêm.

Ví dụ

Input 1

10 1
bbabdcccaa

Output 1

6

Input 2

3 2
abc

Output 2

4

Giải thích

Ở ví dụ ~1~, ta được xâu ~T~ là ~bbabdcccaa~. Sau đó biến tất cả kí tự ~a~ thành ~c~ vì ở vị trí thứ ~8~ kí tự ~c~ liền kề với kí tự ~a~ ở vị trí ~9~ và được xâu mới là ~bbcbdccccc~. Ta được 6 kí tự ~c~ trong xâu mới này nên kết quả in ra là 6.

Ở ví dụ ~2~, ta được xâu ~T~ là ~abcabc~. Sau đó biến tất cả kí tự ~a~ thành ~c~ vì ở vị trí thứ ~3~ kí tự ~a~ liền kề với kí tự ~c~ ở vị trí ~4~ và được xâu mới là ~cbccbc~. Ta được 4 kí tự ~c~ trong xâu mới này nên kết quả in ra là 4.

~ABC~ là một thầy giáo dạy toán nổi tiếng, đối với thầy, chỉ có hai loại số duy nhất là số nguyên tố và hợp số. Lớp học của thầy gồm ~n~ học sinh được đánh thứ tự từ ~1~ tới ~n~. Học sinh thứ ~i~ có mã số là ~a_i~ ~(1≤a_i≤3×10^5)~. Chú ý rằng ở đây các bạn học sinh không nhất thiết là có mã số khác nhau.

Một ngày nọ, thầy đến lớp và mang theo vô số viên kẹo. Thầy sẽ có ~q~ lượt phát kẹo, ở mỗi lượt thầy sẽ chọn một số nguyên dương ~t~ ~(1≤t≤2)~ và ba số nguyên dương ~l,r,v (1≤l≤r≤n; 1≤ v≤10^9)~. Thầy sẽ đi phát cho tất cả các bạn học sinh có số thứ tự ~i~, sao cho ~i∈[l,r]~, đúng ~v~ viên kẹo mỗi bạn. Tuy nhiên, thầy bỗng thấy cách chia kẹo này không thú vị, và quyết định rằng nếu ~t=1~, thầy sẽ chỉ phát kẹo cho các bạn thỏa mãn điều kiện vừa rồi đồng thời mã số ~a_i~ của bạn ấy là số nguyên tố. Ngược lại, nếu ~t=2~, thầy sẽ chỉ đi phát kẹo cho các bạn với mã số ~a_i~ là hợp số.

Sau ~q~ lượt phát kẹo, thầy muốn biết mỗi bạn học sinh có số kẹo là bao nhiêu. Do thầy chỉ dạy toán chứ không phải tin, thầy muốn nhờ các bạn lập trình tính hộ số kẹo của từng bạn.

Lưu ý ở đây ta tạm coi ~1~ là hợp số.

Input

-Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~q~ ~(1≤ n,q≤10^5)~; -Dòng thứ hai gồm ~n~ số nguyên dương ~a_1,a_2,…,a_n~ miêu tả mã số học sinh từ ~1~ tới ~n~. -~q~ dòng sau, mỗi dòng gồm bốn số nguyên dương ~t,l,r,val (1 \le t \le 2; 1≤l \le r≤10^5; 1 \le val≤10^9)~.

Output

• In ra một dòng ~n~ số nguyên dương là số kẹo của từng bạn học sinh.

Subtask

• Có ~20\%~ số test tương ứng với số điểm có ~n,q \le 100~
• Có ~30\%~ số test khác tương ứng với số điểm có ~n,q \le 10^4~
• Có ~30\%~ số test còn lại tương ứng với số điểm có: ~a_i~ đều là số nguyên tố.
• Có ~20\%~ số test còn lại tương ứng với số điểm không có giới hạn gì thêm.

Ví dụ

Input 1

6 3
1 2 4 3 7 10
1 2 5 2
2 1 6 1
2 5 5 4

Output 1

1 2 1 2 2 1

Giải thích 1

Ở lượt đầu tiên, ta chỉ phát kẹo cho các học sinh trong đoạn ~[2,5]~ với mã số là số nguyên tố, đó là ba bạn thứ ~2,4,5~.

Ở lượt thứ hai, ta phát kẹo cho các bạn trong đoạn ~[1,6]~ với mã số là hợp số, đó là các vị trí ~1,3,6~.

Ở lượt thứ ba, ta không thể phát kẹo cho bạn thứ ~5~ vì mã số của bạn là ~7~, đó không phải hợp số.

Cho dãy ~a~ nguyên dương gồm ~n~ phần tử. Ta định nghĩa hàm ~f(l,r)~ như sau: ~f(l,r) = 1\times a[l] + 2\times a[l+1] + 3\times a[l+2] + ... (r-l+1)\times a[r]~.

Có ~q~ truy vấn, mỗi truy vấn gồm hai số ~l~, ~r~ với ~1 \le l \le r \le n~. Với mỗi truy vấn, hãy in ra ~f(l,r)~.

Input

• Dòng đầu gồm 2 số nguyên dương ~n~ và ~q~. ~(1 \le n, q \le 10^5)~
• Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy ~a~. ~(1 \le a[i] \le 10^5)~.
• ~q~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên dương ~l~, ~r~ miêu tả các truy vấn.

Ouput

• In ra ~q~ dòng, mỗi dòng là kết quả của một truy vấn tương ứng.

Subtask

• Subtask ~1~: ~n,q \le 2 \times 10^3~ ~(30\%)~
• Subtask ~2~: Trong tất cả các truy vấn, ~l=1~.
• Subtask ~3~: Không giới hạn gì thêm ~(40\%)~.

Sample Test

Input

4 3
1 2 3 4
1 2
2 3
1 4 

Output

5
8
30

Cho ~t~ truy vấn và giá trị ~mod~ ~(1 \le mod \le 2*10^9)~, mỗi truy vấn gồm hai số nguyên dương ~n~, ~k~. Kí hiệu ~C(k,n)~ là tổ hợp chập ~k~ của ~n~, hãy in ra ~C(k,n)~ cho mỗi truy vấn tương ứng. Do kết quả có thể rất lớn nên hãy in nó sau khi lấy phần dư cho ~mod~.

Subtask

• Sub ~1~: ~t \le 10^5~, ~1 \le k \le n \le 2000~. (30%)
• Sub ~2~: ~t = 1~, ~1 \le k \le n \le 10^5~. (30%)
• Sub ~3~: ~t \le 10^5~, ~1 \le k \le n \le 10^5~, ~mod = 10^9+7~. (40%)

Input

• Dòng đầu tiên gồm một số nguyên dương ~sub~ miêu tả subtask mà test này tương ứng. (~1 \le sub \le 3~)
• Dòng thứ hai gồm hai số nguyên dương ~t~ và ~mod~.
• ~t~ dòng sau, mỗi dòng gồm hai số nguyên dương ~n~, ~k~ (~k \le n~) miêu tả truy vấn tương ứng.

Output

• In ra ~t~ dòng, mỗi dòng là kết quả của truy vấn tương ứng.

Sample Test

Input:

1
3 2345
6 4
8 4
15 8

Output:

15
70
1745

Định nghĩa ~f(x)~ là tổng các chữ số của số nguyên ~x~. Cho số nguyên ~k~, hãy tìm giá trị ~f(x)~ nhỏ nhất có thể khi xét các số nguyên dương ~x~ chia hết cho ~k~.

Input

• Gồm một số nguyên ~2 \le k \le 100000~.

Output

• In ra giá trị ~f(x)~ nhỏ nhất.

Sample Test

Input:

6

Output:

3

Sủi là người có máu M nên layout 40% là chưa đủ khổ dâm. Sủi làm một chiếc bàn phím mới có dạng ~m~ chữ cái đầu của bảng chữ cái tiếng Anh nằm cạnh nhau. Cậu cần đánh một đoạn văn bản ~s~ có độ dài ~n~ chỉ gồm các chữ cái trong bàn phím. Sủi sẽ gõ từng chữ lần lượt theo thứ tự từ trái sang phải và chi phí để di chuyển từ một chữ sang chữ khác là khoảng cách giữa 2 chữ đó. Chi phí của văn bản là tổng các chi phí di chuyển giữa các chữ hay: ~\sum_{i=1}^{n - 1} | p_{s_{i + 1}} - p_{s_i} | ~ với ~p_x~ là vị trí kí tự ~x~ từ trái sang phải của bàn phím.

Input

• Dòng đầu gồm 2 số ~n~ và ~m~.
• Dòng tiếp theo là xâu gồm ~n~ kí tự chứa ~m~ kí tự đầu tiên trong bảng chữ cái tiếng Anh.

Output

• In ra một số nguyên duy nhất là chi phí nhỏ nhất có thể.

Sample Test

Input:

6 3
aacabc

Output:

5

Giải thích:

• Sắp xếp thành bac

Ràng buộc

• Subtask 1: ~1 \le n \le 100, 1 \le m \le 10~ (40% số điểm).
• Subtask 2: ~1 \le n \le 100000, 1 \le m \le 10~ (30% số điểm).
• Subtask 3: ~1 \le n \le 100000, 1 \le m \le 20~ (30% số điểm).

Đếm số cách chia ~n~ cái kẹo cho ~k~ người sao cho số kẹo của mỗi người nhận được đều thuộc đoạn ~[L,H]~. Hai cách chia kẹo được coi là khác nhau nếu tồn tại một người nhận được số kẹo khác nhau trong hai cách.

Nói cách khác, đếm số nghiệm nguyên của phương trình: ~x_1 + x_2 + ... + x_k = n~, sao cho ~\forall i \in [1,n]: L \le x_i \le H~.

Input

• Gồm bốn số nguyên dương: ~n~ ~k~ ~L~ ~H~ ~(0 \le L \le H \le n)~

Constraint

• ~1 \le k \le n \le 10^6~

Subtask

• Subtask ~1~ ~(30\%)~: ~1 \le n \le 10~.
• Subtask ~2~ ~(30\%)~: ~k \le n \le 1000~
• Subtask ~3~ ~(40\%)~: ~k \le n \le 10^6~

Output

• In ra kết quả bài toán sau khi chia lấy dư cho ~10^9+7~.

Sample Input 1:

6 3 0 6 

Sample Output 1:

28

Sample Input 2:

6 4 0 2 

Sample Output 2:

10