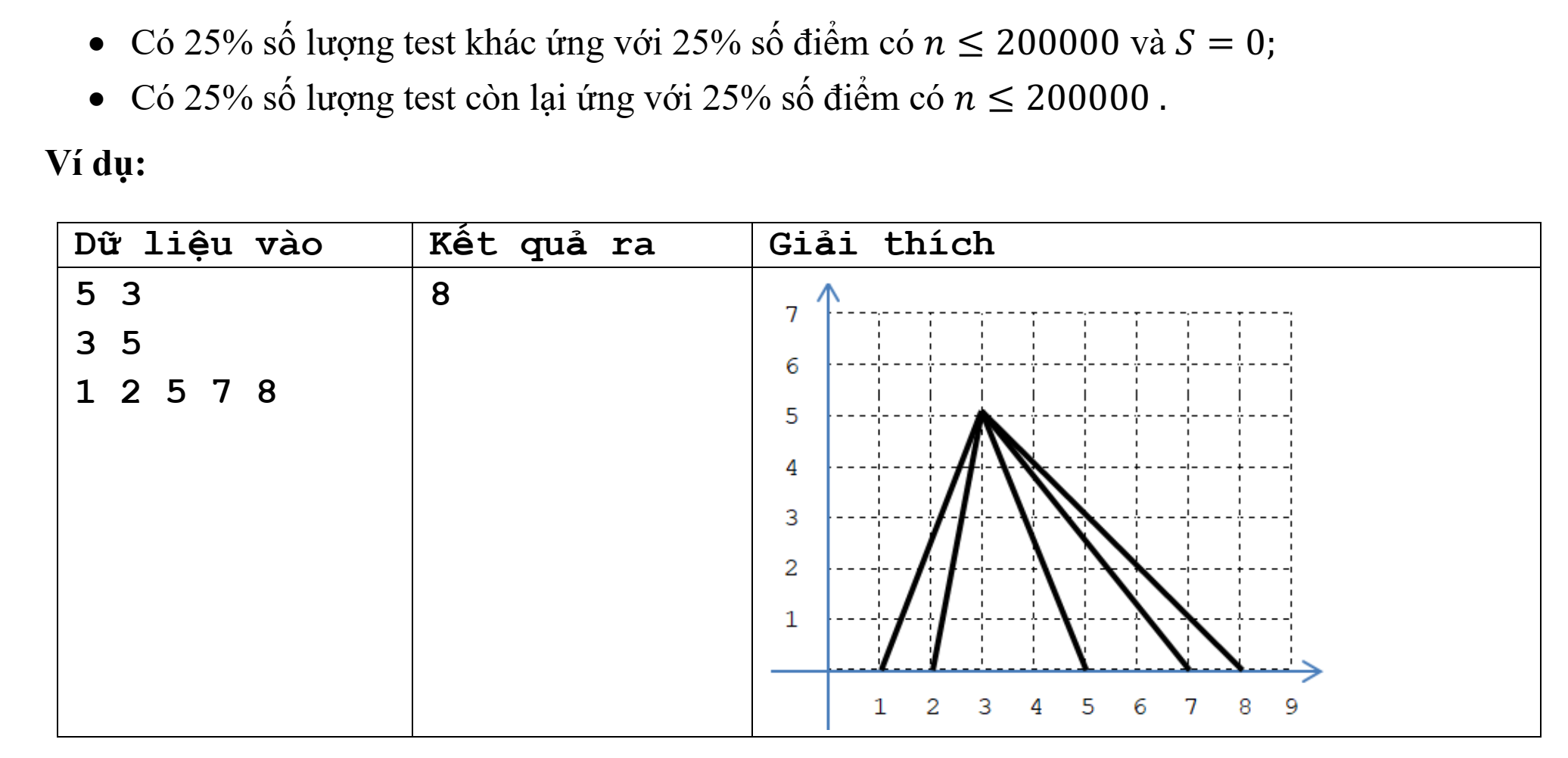
Trong phòng thí nghiệm chỉ có đúng ba loại cốc có dung tích là ~5 \ (ml)~, ~3 \ (ml)~ và ~2 \ (ml)~. Hỏi cần ít nhất bao nhiêu lần đong nước để lấy được đúng ~N \ (ml)~.

Dữ liệu:

Một số nguyên dương duy nhất ~N~ ~(2 \le N \le 10^{18})~ là số nước cần đong.

Kết quả:

Một số nguyên dương duy nhất là số lượng lần đong ít nhất thoả mãn yêu cầu đề bài.

Ví dụ

Input

12

Output

3

Giải thích

Đong hai lần bằng cốc ~5 \ (ml)~ và một lần bằng cốc ~2 \ (ml)~.

Input

6

Output

2

Giải thích

Đong hai lần bằng cốc ~3 \ (ml)~.

Cho ~2~ số nguyên ~A~ và ~B~. Tìm số nguyên ~M~ nằm giữa ~A~ và ~B~ sao cho khoảng cách giữa ~A \times M~ và ~B \times M~ là nhỏ nhất. ~M~ phải khác ~A~ và ~B~

Input

• Gồm 1 dòng duy nhất chứa hai số nguyên ~A~ và ~B~ ~(-10^{9} \leq A \leq B \leq 10^{9})~
• Dữ liệu đảm bảo ~A \le B-2~

Output

• Gồm 1 dòng duy nhất chứa số nguyên ~M~ cần tìm.

Example

Sample input 1

1 3

Sample output 1

2

Cho một dãy số gồm ~N~ số nguyên dương ~a_1, a_2, ..., a_N~ có giá trị không vượt quá ~10^6~. Tìm dãy con liên tiếp ngắn nhất có chứa ít nhất hai số nguyên tố.

Dữ liệu:

• Dòng đầu tiên gồm một số nguyên dương ~N \ (N \le 10^6)~ là số lượng phần tử của dãy số;
• Dòng thứ hai gồm ~N~ số nguyên dương ~a_1, a_2, ..., a_N~ lần lượt mô tả các phần tử của dãy số.

Kết quả:

Một số nguyên duy nhất là số lượng phần tử của dãy con thoả mãn đề bài. Trường hợp không tồn tại dãy con thoả mãn, in ra ~-1~.

Ví dụ

Input

10
3 4 8 4 5 6 1 7 4 6

Output

4

Giải thích

Chọn dãy con từ vị trí thứ ~5~ đến vị trí thứ ~8~: ~5, 6, 1, 7~.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm của bài thoả mãn: ~N \le 10^3; \ a_i \le 10^3~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thoả mãn: ~N \le 10^6; \ a_i \le 10^3~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Cho hai điểm ~A~, ~B~ trên trục Ox có toạ độ nguyên. Tìm hai điểm ~X~, ~Y~ có toạ độ nguyên trên trục Ox sao cho hai điểm này chia đoạn thằng ~AB~ thành ba phần có độ dài bằng nhau. Nếu không tồn tại hai điểm như trên, in ra ~-1~.

Input

Gồm một dòng duy nhất chứa hai số nguyên ~a~, ~b~ (~1 \le a < b \le 10^9~) lần lượt mô tả toạ độ của điểm ~A~ và toạ độ của điểm ~B~.

Output

Nếu tồn tại hai điểm ~X~, ~Y~ như trên, in ra hai số nguyên ~x~, ~y~ (~x \le y~) lần lượt là toạ độ của hai điểm ~X~, ~Y~ tìm được, ngược lại in ra ~-1~.

Example

Input 1

1 4

Output 1

2 3

Input 2

2 6

Output 2

-1

Cho một robot được lập trình di chuyển trên một hàng ngang gồm các ô vuông. Mỗi ô được đặt tên bằng các kí tự theo thứ tự từ ~'𝐴'~ đến ~'𝑍'~ và được lặp lại vô hạn. Ban đầu robot xuất phát ở ô thứ ~1~ có tên là ~'𝐴'~ và nhảy đến các ô tiếp theo quy luật: lần ~1~ nhảy ~1~ ô, lần ~2~ nhảy ~2~ ô, lần ~3~ nhảy ~3~ ô, ~…~, lần ~𝑁~ nhảy ~𝑁~ ô. Vậy sau ~𝑁~ lần nhảy thì robot đang ở ô nào?

Dữ liệu:

Gồm một số nguyên dương ~N~ là số lần nhảy của robot ~(N \le 10^9)~.

Kết quả:

Một kí tự duy nhất là tên của ô sau ~N~ lần robot nhảy.

Ràng buộc

• Có ~60\%~ số test ứng với ~60\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10^3;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10^6;~
• ~20\%~ số test còn lại ứng với 20% số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

1

Output

B

Giải thích: Sau ~1~ lần nhảy, robot ở ô thứ ~2~, có tên là kí tự ~B~.

Input

4

Output

K

Giải thích: Sau ~4~ lần nhảy, robot ở ô thứ ~11~, có tên là kí tự ~K~.

Input

7

Output

C

Giải thích: Sau ~7~ lần nhảy, robot ở ô thứ ~29~, có tên là kí tự ~C~.

Chuẩn bị Gala mừng năm mới Tết Tân Sửu 2021 của công ty HiTech, ban giám đốc quyết định có giải thưởng đặc biệt cho thành viên của công ty. Sau khi đưa ra các tiêu chí đánh giá, việc bầu chọn sẽ được thực hiện bằng cách tất cả các thành viên sẽ được bỏ phiếu cho nhau.

Hình thức bỏ phiếu được thực hiện thông qua phiếu bầu chọn online. Danh sách các thành viên của công ty được niêm yết và quy định là số thứ tự từ ~1~ đến ~N~ ~(1≤N≤5000),~ tương ứng với ~N~ ô trên phiếu bầu chọn. Sau khi thực hiện, ban tổ chức thu được các danh sách phiếu tương ứng của các thành viên công ty. Trong mỗi phiếu bầu chọn, giá trị ô ở vị trí tương ứng ghi ~'X'~ là bầu chọn cho người đó, ô ghi ~'0'~ là không bầu chọn (coi các trường hợp bầu chọn không hợp lệ là không bầu chọn).

Yêu cầu: Em hãy giúp ban tổ chức đưa ra danh sách các nhân viên có phiếu bầu chọn cao nhất.

Dữ liệu:

• Dòng đầu tiên gồm số một số nguyên dương ~N~ ~(1≤N≤5000)~ là số lượng phiếu bầu chọn.
• ~N~ dòng tiếp theo mỗi dòng tương ứng là ~N~ giá trị của các phiếu đã bầu chọn.

Các kí tự cách nhau một dấu cách.

Kết quả:

• Dòng đầu tiên ghi số lượng người được nhiều phiếu nhất và số lượng phiếu.
• Dòng thứ hai ghi thứ tự tương ứng của những người được cao phiếu nhất đó theo thứ tự tăng dần.

Ví dụ

Input

5
X 0 X 0 X
X 0 0 X X
0 0 X 0 0
0 X 0 X 0
0 0 X X 0

Output

2 3
3 4

Giải thích:

• Người số ~1~ được ~2~ phiếu bầu chọn.
• Người số ~2~ được ~1~ phiếu bầu chọn.
• Người số ~3~ được ~3~ phiếu bầu chọn.
• Người số ~4~ được ~3~ phiếu bầu chọn.
• Người số ~5~ được ~2~ phiếu bầu chọn.
• Người số ~3~ và số ~4~ cùng được số phiếu bầu chọn lớn nhất.

Giới hạn

• Có ~70\%~ số test tương ứng với số điểm có ~N \le 1000;~
• ~30\%~ số test còn lại tương ứng với số điểm có ~N \le 5000.~

Cho hàm ~f(x)~ nhận đầu vào ~x~ là số nguyên không âm được định nghĩa như sau:

• Nếu ~x<10, f(x)=x~
• Ngược lại ~f(x)=f(D(x))~ với ~D(x)~ là tổng các chữ số trong biểu diễn thập phân của ~x~.
• Cho số nguyên dương ~n~, hãy tính ~f(n)~ .

Input:

Gồm một dòng duy nhất chứa số nguyên n ~(1≤n<10^{100000}).~

Output:

In ra một số nguyên là kết quả.

Sample Input 1

4

Sample Output 1

4

Đây là phiên bản khó hơn của bài PA120. Điểm khác biệt duy nhất giữa hai bài là số ~k~ và giới hạn các số.

Sau khi bán hết sách, TDZ chuyển sang mở một quán cà phê.

Qua thăm dò, TDZ đã biết trước ngày khai trương sẽ có ~n~ khách, khách thứ ~i~ sẽ vào thời điểm ~h_i~. Để phục vụ lượng khách đến dồn dập, quán cà phê có thuê thêm một số nhân viên ưu tú. Mỗi nhân viên có thể hoạt động không ngừng nghỉ, mỗi lần chỉ phục vụ một khách trong đúng ~k~ đơn vị thời gian. Nhưng nếu một vị khách tới mà không nhận được sự phục vụ ngay thì sẽ lập tức bỏ đi.

Cụ thể, một vị khách đến ở thời điểm ~x~ nào đó, thì nhân viên sẽ phục vụ xong cho vị khách đó ở thời điểm ~x + k~. Khách đó sẽ rời quán và nhân viên tiếp tục phục vụ luôn khách tiếp theo (nếu có).

Hãy giúp TDZ tìm ra số lượng nhân viên cần thuê ít nhất mà vẫn đảm bảo tất cả các khách đều được phục vụ.

Input

• Dòng đầu tiên chứa 2 số nguyên dương ~n~, ~k~ (~n \leq 10^6, k \leq 10^9~).
• Dòng tiếp theo chứa ~n~ số nguyên dương ~h_1, h_2, h_3, \ldots, h_n~ tương ứng với thời điểm khách đến (~h_i \leq 10^9~).

Output

In ra số lượng nhân viên ít nhất cần thuê.

Subtasks

• Subtask ~1~ (~25\%~): ~n \leq 10^3~.
• Subtask ~2~ (~37.5\%~): ~n \leq 10^6, h_i \leq 10^6~.
• Subtask ~3~ (~37.5\%~): Không có điều kiện gì thêm.

Sample Test

Input:

5 2
1 2 5 3 5

Output:

2

Note: Thuê hai nhân viên:

• Nhân viên thứ nhất sẽ phục vụ khách thứ nhất, rồi đến khách thứ tư và cuối cùng phục vụ khách thứ ba.
• Nhân viên thứ hai phục vụ khách thứ hai rồi đến khách thứ năm.