An đang học xem giờ trên đồng hồ treo tường.
Giả sử hiện tại là 11 giờ 59 phút, hỏi sau ~T~ phút thì kim phút đi qua chính giữa số 12 bao nhiêu lần?

Yêu cầu:
Cho số phút ~T~, hãy đếm xem trong khoảng thời gian đó kim phút đi qua số 12 được bao nhiêu lần.

Input

• Một số nguyên dương ~T~
  > ~(1 \leq T \leq 10^9)~

Output

• Một số nguyên duy nhất là kết quả của bài toán.

Sample Test

Input

1

Output

1

Input

89

Output

2

Note

• Mỗi 60 phút kim phút quay đúng một vòng và đi qua vị trí 12
• Nhưng vì bắt đầu tại ~11:59~, nên phút đầu tiên đã đi qua vị trí 12
  → Mỗi lần tròn 60 phút lại đi qua thêm một lần nữa.

Cho xâu ~S~ chỉ gồm hai kí tự ~'a'~ và ~'b'~.
Xâu ~XS~ là xâu được tạo bởi ghép ~X~ lần xâu ~S~ liền với nhau.

Yêu cầu:
Hãy đếm xem có bao nhiêu xâu con "ab" xuất hiện trong xâu ~XS~.

Input

• Gồm hai dòng:
  
  • Dòng thứ nhất chứa xâu ~S~ có độ dài ~N~
  • Dòng thứ hai chứa số nguyên dương ~X~
    > ~(0 < N \leq 10^3;~ ~0 < X \leq 10^9)~

Output

• Một số nguyên duy nhất là kết quả của bài toán.

Subtasks

• Subtask 1 (~50\%~ số điểm): ~N, X \leq 50~
• Subtask 2 (~30\%~ số điểm): ~N, X \leq 10^3~
• Subtask 3 (~20\%~ số điểm): Không có ràng buộc gì thêm.

Sample Test

Input

aabb
2

Output

2

Input

baba
2

Output

3

Input

aaa
1

Output

0

Note

• Test 1: ~XS = aabbaabb~, có 2 xâu con "ab"
• Test 2: ~XS = babababa~, có 3 xâu con "ab"
• Test 3: ~XS = aaa~, không có "ab"

Cho một chuỗi kí tự gồm các kí tự chữ viết hoa, có bao nhiêu cách chọn ra bộ kí tự AMS khác nhau. Các kí tự được chọn phải để theo thứ tự trước sau như ban đầu.

Ví dụ, với câu CHAO AMS có ~2~ bộ kí tự AMS, tính theo vị trí là ~(3, 7, 8)~ và ~(6, 7, 8)~.

Input

Nhập vào một xâu văn bản ~S~ có tối đa ~10^6~ kí tự. Các kí tự đều là chữ in hoa.

Output

Ghi ra số cách chọn bộ kí tự AMS.

Ví dụ

Input

CHAO AMS

Output

2

Input

AMSER IN AMS

Output

4

Nhân dịp kênh YouTube của TDZ được ~100~ triệu subscribers, chủ kênh T giấu tên quyết định mở một cuộc giveaway lớn nhất trong lịch sử. Cụ thể, sẽ có ~n~ subscribers được chọn và mỗi subscriber này sẽ nhận được một mã số ~a_i~ và một hộp quà có giá trị là ~b_i \ (1 \le i \le n)~.

Kênh YouTube TDZ được thành lập để truyền tải những thông điệp nhân văn nên nhân dịp giveaway này, T đã lập quỹ giấu tên để mọi người có thể cùng giúp đỡ và tạo điều kiện cho những người có hoàn cảnh khó khăn. T định nghĩa một cặp subscribers là cặp "may mắn" nếu tổng giá trị hai mã số của cặp này lớn hơn tổng giá trị hai hộp quà mà cặp này đang sở hữu. Nói cách khác, cặp ~(i, j) \ (1 \le i, j \le n)~ là cặp "may mắn" nếu ~a_i + a_j > b_i + b_j~. Với mỗi cặp "may mắn" mà T tìm được, T sẽ quyên góp ~1 \ \text{USD}~ vào quỹ từ thiện giấu tên.

Hãy giúp T tính số tiền mà anh ấy sẽ quyên góp vào quỹ từ thiện của mình.

Input

• Dòng đầu tiên chứa số nguyên dương ~n \ (n \ge 2);~
• Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, ..., a_n \ (1 \le a_i \le 10^5, \ 1 \le i \le n);~
• Dòng thứ ba chứa ~n~ số nguyên ~b_1, b_2, ..., b_n \ (1 \le b_i \le 10^5, \ 1 \le i \le n).~

Output

In ra kết quả là số tiền (đơn vị ~\text{USD}~) mà T sẽ quyên góp vào quỹ giấu tên trong sự kiện giveaway này.

Scoring

• Subtask 1 [20%]: ~n \le 1000;~
• Subtask 2 [80%]: ~n \le 10^5.~

Examples

Input

4
3 2 4 5
2 3 6 4

Output

1

Giải thích: Cặp ~(1, 4)~ là cặp subscribers "may mắn".

Input

4
3 2 4 5
2 2 6 4

Output

3

Giải thích: Các cặp ~(1, 2), (1, 4), (2, 4)~ là các cặp subscribers "may mắn".

Trên mặt phẳng toạ độ Oxy, bạn nhận được một hình vuông với cạnh song song với trục toạ độ, có góc trái dưới là ~(0, 0)~ và góc phải trên là ~(n, n)~. Hãy đếm xem có bao nhiêu điểm toạ độ nguyên nằm trong hoặc nằm trên biên hình vuông mà có khoảng cách Manhattan đến ~(x_0, y_0)~ đúng bằng ~k~.

Khoảng cách Manhattan giữa hai điểm ~(x, y)~ và ~(u, v)~ được tính bằng ~|x - u| + |y - v|~.

Input

Gồm một dòng duy nhất chứa bốn số nguyên ~n~, ~x_0~, ~y_0~, ~k~ (~1 \le n, k \le 10^{18}~; ~1 \le x_0, y_0 \le n~).

Output

In ra một số nguyên là số điểm toạ độ nguyên nằm trong hoặc nằm trên biên hình vuông mà có khoảng cách Manhattan đến ~(x_0, y_0)~ đúng bằng ~k~.

Scoring

• Subtask ~1~ (~30\%~ số điểm): ~n \le 10^3~.
• Subtask ~2~ (~30\%~ số điểm): ~k \le 10^5~.
• Subtask ~3~ (~40\%~ số điểm): Không có ràng buộc gì thêm.

Example

Input

4 1 1 2

Output

6

Bản đồ thành phố X có dạng lưới ô vuông ~M~ hàng ~N~ cột, các hàng được đánh số từ ~1~ tới ~M~, các cột được đánh số từ ~1~ tới ~N~. Mỗi ô vuông trên bản đồ có thể là khu đất trống hoặc một khu dân cư hoặc một siêu thị.

Mỗi siêu thị chỉ có thể phục vụ các khu dân cư có khoảng cách so với nó không quá ~D~, nghĩa là nếu siêu thị nằm ở ô ~(x, y)~ thì nó có thể phục vụ được tất cả các khu dân cư nằm trong hình vuông có ô trái trên là ~(x - D, y - D)~, ô phải dưới là ~(x + D, y + D)~ (như Hình 1).

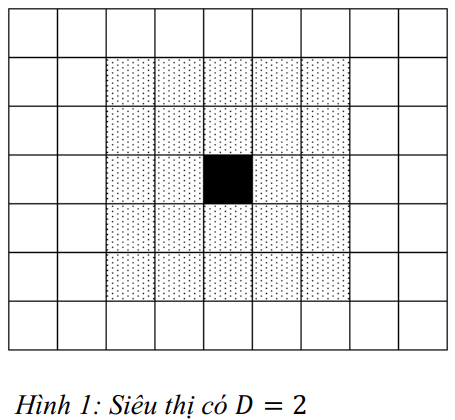
Một khu dân cư gọi là "chất lượng cao" nếu được ít nhất ~K~ siêu thị có thể phục vụ nó. Cho biết bản đồ của thành phố X, hãy đếm số lượng khu dân cư "chất lượng cao".

Dữ liệu vào từ file văn bản KHUDANCU.INP:

• Dòng đầu chứa bốn số nguyên ~M, N, D~ và ~K~ ~(1\le D \le \max(M, N); \ 1\le K\le M \times N)~;
• ~M~ dòng tiếp theo, mỗi dòng gồm ~N~ ký tự, mỗi ký tự biểu diễn một ô vuông bản đồ. Mỗi ký tự sẽ thuộc một trong ba loại sau:
  • . biểu diễn một khu đất trống;
  • P biểu diễn một khu dân cư;
  • M biểu diễn một siêu thị;

Dữ liệu đảm bảo tồn tại ít nhất một khu dân cư và ít nhất một siêu thị.

Kết quả ghi ra file văn bản KHUDANCU.OUT:

Ghi ra một số duy nhất là số khu dân cư "chất lượng cao".

Ví dụ

Input

5 5 1 2
P....
....P
..PM.
.M...
.....

Output

1

Giải thích

Bản đồ minh hoạ thành phố ~X~ như Hình 2.

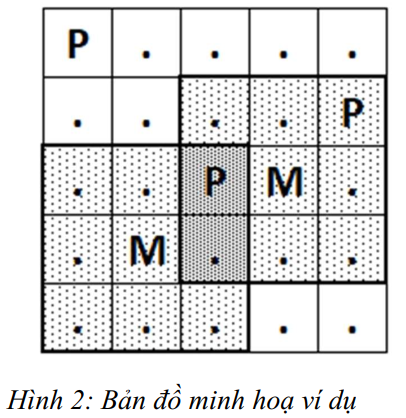
Khu dân cư ở ô ~(1, 1)~ không được siêu thị nào phục vụ;

Khu dân cư ở ô ~(2, 5)~ được một siêu thị có thể phục vụ;

Khu dân cư ở ô ~(3, 3)~ được hai siêu thị có thể phục vụ;

Vậy có một khu dân cư "chất lượng cao".

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thoả mãn: ~M = 1; \ N, D \le 10^3~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~M = 1; \ N \le 10^5~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~2 \le M, N \le 1000;~ số khu dân cư, số siêu thị không vượt quá ~1000~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài thoả mãn: ~2 \le M, N \le 1000~.

An có một xâu ký tự ~S~ có độ dài ~N~, chỉ gồm các chữ cái Latin in thường. An muốn tìm một xâu con liên tiếp không rỗng của xâu ~S~ sao cho chênh lệch giữa số lần ký tự xuất hiện nhiều nhất và số lần ký tự xuất hiện ít nhất ở trong xâu con là lớn nhất. Lưu ý rằng, ký tự xuất hiện ít nhất phải xuất hiện ít nhất một lần trong xâu con.

Dữ liệu vào từ file văn bản CHENHLECH.INP:

• Dòng đầu tiên chứa số nguyên ~N~ ~(1\le N\le 10^6)~ là độ dài của xâu ~S~;
• Dòng thứ hai chứa xâu ~S~.

Kết quả ghi ra file văn bản CHENHLECH.OUT:

Một số nguyên duy nhất là chênh lệch lớn nhất của xâu con tìm được.

Ví dụ

Input

6
caabac

Output

2

Giải thích

Có thể chọn xâu con: aaba hoặc caaba hoặc aabac hoặc caabac.

Input

3
ttt

Output

0

Giải thích

Có thể chọn xâu con: ttt hoặc tt hoặc t.

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thoả mãn: ~N \le 10^2~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thoả mãn: ~N \le 10^5~;
• ~30\%~ số test còn lại ứng với ~30\%~ số điểm của bài không có ràng buộc gì thêm.