NCOL2 - T12
Xuất hiện
Nộp bàiPoint: 100
Cho dãy ~a~ có ~m~ số nguyên ~a_1, a_2, \ldots, a_m~.
Dãy ~b~ có ~n~ số nguyên ~b_1, b_2, \ldots, b_n~. Hãy tìm số lượng phần tử trong dãy ~a~ xuất hiện trong dãy ~b~.
Input
Dòng đầu tiên chứa hai số nguyên ~m~ và ~n~ ~(0 < m, n \leq 10^5)~.
Dòng tiếp theo chứa ~m~ số nguyên ~a_i~ ~(-10^9 \leq a_i \leq 10^9)~.
Dòng tiếp theo chứa ~n~ số nguyên ~b_i~ ~(-10^9 \leq b_i \leq 10^9)~.
Output
Số lượng phần tử trong dãy ~a~ xuất hiện trong dãy ~b~.
Sample
Input
3 5
1 2 3
1 3 3 4 5
Output
2
Xâu đẹp
Nộp bàiPoint: 100
Xâu đẹp là xâu có nhiều nhất một ký tự có số lần xuất hiện là lẻ. Cho xâu ~S~ có độ dài ~n~ chỉ gồm các chữ cái thường ~S_0S_1 \dots S_{n-1}~. Một đoạn ~(i,j)~ của xâu ~S~ là xâu: ~S_iS_{i+1} \dots S_j~.
Yêu cầu: Với mỗi đoạn ~(i,j)~, hãy xác định số ký tự ít nhất cần thay đổi để đoạn ~(i,j)~ thành xâu đẹp.
Input
- Dòng đầu tiên chứa hai số nguyên ~n~ và ~Q~ (~n,Q \leq 10^6~) - lần lượt là độ dài xâu và số lượng truy vấn.
- Dòng thứ hai chứa xâu ~S~.
- ~Q~ dòng tiếp theo, mỗi dòng chứa hai số ~i~ và ~j~ (~0 \leq i \leq j \leq n - 1~) - xác định một đoạn trong xâu ~S~ cần biến đổi.
Output
Gồm ~Q~ dòng lần lượt là kết quả của ~Q~ truy vấn.
Sample Test
| Input | Output |
|---|---|
| 8 3 abcaacba 1 3 2 7 1 6 |
1 1 0 |
Note
- Đoạn [~1,3~] của xâu ~S~ là "bca". Có thể thay đổi kí tự 'c' thành kí tự 'b', ta được xâu "bba" thỏa mãn.
- Đoạn [~2,7~] của xâu ~S~ là "caacba". Có thể thay đổi kí tự 'b' thành kí tự 'a', ta được xâu "caacaa" thỏa mãn.
- Đoạn [~1,6~] của xâu ~S~ là "bcaacb". Đây là xâu đẹp rồi nên không cần biến đổi.
CSES - Weird Algorithm | Thuật toán lạ
Nộp bàiPoint: 100
Xét thuật toán sau nhận đầu vào là một số nguyên dương ~n~. Nếu ~n~ chẵn, thuật toán sẽ chia nó cho hai, và nếu ~n~ lẻ, thuật toán nhân ba nó lên rồi cộng thêm một đơn vị. Thuật toán trên lặp lại điều này cho tới khi ~n~ bằng ~1~.
Ví dụ, dãy số thực hiện với ~n=3~ là:
~3 → 10 → 5 → 16 → 8 → 4 → 2 → 1~
Việc của bạn là hãy mô phỏng lại cách hoạt động của thuật toán với một giá trị ~n~ cho trước.
Input:
- Một dòng duy nhất chứa số ~n~.
Output:
- In ra một dòng lần lượt chứa từng giá trị của ~n~ trong khi chạy thuật toán.
Constraints
- ~1 \le n \le 10^6~
Sample Test
| Input | Output |
|---|---|
| 3 | 3 10 5 16 8 4 2 1 |
CSES - Missing Number | Số còn thiếu
Nộp bàiPoint: 100
Cho một dãy số chứa các số ~1, 2, 3, \ldots, n~ trừ một số. Hãy tìm số đó.
Input
- Dòng đầu tiên gồm một số nguyên dương ~n~ (~2 \leq n \leq 2 \times 10^5~).
- Dòng tiếp theo chứa ~n - 1~ số trong khoảng từ ~1~ đến ~n~.
Output
- In ra số còn thiếu.
Sample Test
Input:
5
2 3 1 5
Output:
4
CSES - Repetitions | Lặp lại
Nộp bàiPoint: 100
Cho một dãy DNA gồm các kí tự A, C, G, T.
Nhiệm vụ của bạn là tìm đoạn lặp lại dài nhất trong dãy (đoạn gồm nhiều các kí tự giống nhau nhất).
Input
- Gồm một xâu kí tự duy nhất gồm ~n~ kí tự (~1 \leq n \leq 10^6~).
Output
- In ra độ dài của đoạn lặp lại dài nhất.
Sample Test
Input:
ATTCGGGA
Output:
3
CSES - Increasing Array | Dãy tăng
Nộp bàiPoint: 100
Cho một dãy số gồm ~n~ số nguyên. Bạn muốn sửa dãy thành một dãy không giảm (số đứng sau lớn hơn hoặc bằng số đứng trước).
Ở mỗi bước bạn có thể tăng một số bất kỳ lên ~1~ đơn vị. Hỏi số bước ít nhất cần thiết cần thực hiện là bao nhiêu?
Input
- Dòng đầu tiên gồm một số nguyên dương ~n~ (~1 \leq n \leq 2 \times 10^5~).
- Dòng tiếp theo chứa ~n~ số nguyên ~a_1, a_2, a_3, \ldots, a_n~ (~1 \leq a_i \leq 10^9~).
Output
- In ra số bước tối thiểu.
Sample Test
Input:
5
3 2 5 1 7
Output:
5
Số hoàn hảo
Nộp bàiPoint: 100
Một số nguyên dương ~A~ được gọi là hoàn hảo nếu ~2 \times A \leq K~ (trong đó ~K~ là tổng các ước dương của ~A~).
Ví dụ: số ~12~ được coi là số hoàn hảo vì ~2 \times 12 \leq K~ với ~K = 1 + 2 + 3 + 4 + 6 + 12 = 28~
Cho ~N~ số nguyên dương ~A_1, A_2, \ldots, A_n~, hãy đếm số lượng số hoàn hảo trong dãy đã cho.
Input
- Dòng đầu tiên chứa số nguyên dương ~N~. (~N \leq 10^4~)
- ~N~ dòng tiếp theo, dòng thứ ~i~ chứa số nguyên dương ~A_i~. (~A_i \leq 10^6~)
Output
In ra số lượng số hoàn hảo trong dãy đã cho.
Sample Test
Input:
5
8
16
12
6
7
Output:
2
Số đơn lẻ
Nộp bàiPoint: 100
Cho một dãy gồm ~N~ số nguyên dương ~a_1, a_2, a_3, ..., a_N~. Biết rằng các số trong dãy đều xuất hiện hai lần, trừ một số. Hãy tìm số đó.
Input
- Dòng thứ nhất chứa số nguyên dương ~N~.
- Dòng thứ hai chứa ~N~ số nguyên dương ~a_1, a_2, a_3, ... a_N~. (~a_i \leq 10^6~)
- Các số đều xuất hiện hai lần trừ một số.
Output
- In ra số chỉ xuất hiện một lần trong dãy.
Subtasks
- Subtask 1 (~20\%~ số điểm): ~N = 3~.
- Subtask 2 (~30\%~ số điểm): ~N \leq 10^3~.
- Subtask 3 (~50\%~ số điểm): ~N \leq 10^6~.
Sample Test 1
Input
5
4 1 2 1 2
Output
4
Dãy đối xứng
Nộp bàiPoint: 100
Cho dãy ~A~ gồm ~n~ phần tử, phần tử thứ ~i \ (1 \le i \le n)~ có giá trị ~a_i~.
Bạn có thể biến đổi dãy ~A~ bằng thao tác sau: Chọn hai phần tử liên tiếp trong dãy và thay thế hai phần tử này bằng tổng của chúng.
Hãy đếm số lượng thao tác tối thiểu để dãy ~A~ là dãy đối xứng. Dãy ~A~ được coi là dãy đối xứng nếu đọc từ phải sang trái vẫn thu được dãy ~A~ ban đầu.
Input
- Dòng đầu tiên chứa số nguyên dương ~n;~
- Dòng tiếp theo chứa ~n~ số nguyên dương ~a_i \ (1 \le a_i \le 10^9)~.
Output
In ra kết quả là số thao tác tối thiểu để dãy ~A~ là dãy đối xứng.
Scoring
- Subtask 1 [30%]: ~n \le 10;~
- Subtask 2 [30%]: ~n \le 1000;~
- Subtask 3 [40%]: ~n \le 10^6.~
Examples
Input
3
1 2 3
Output
1
Giải thích: ~\textbf{1 2} \ 3 \rightarrow 3 \ 3.~
Input
5
1 2 4 6 1
Output
1
Giải thích: ~1 \ {\textbf{2 4}} \ 6 \ 1 \rightarrow 1 \ 6 \ 6 \ 1~.
Input
4
1 4 3 2
Output
2
Giải thích: ~\textbf{1 4} \ 3 \ 2 \rightarrow 5 \ \textbf{3 2} \ \rightarrow 5 \ 5~.
CSES - Number Spiral | Xoắn ốc số
Nộp bàiPoint: 100
Một xoắn ốc số là một bảng dài vô hạn có quy luật như sau:
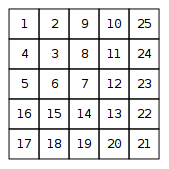
Nhiệm vụ của bạn là đưa ra số trên hàng ~x~ và cột ~y~.
Input
- Dòng đầu tiên gồm một số nguyên dương ~t~ - Số lượng tests (~2 \leq n \leq 10^5~).
- ~t~ dòng tiếp theo, mỗi dòng chứa ~2~ số nguyên ~x~ và ~y~ (~1 \leq x, y \leq 10^9~).
Output
- Với mỗi test, in ra số trên ô ~(x, y)~ trên các dòng khác nhau.
Sample Test
Input:
3
2 3
1 1
4 2
Output:
8
1
15
CSES - Two Knights | Hai quân mã
Nộp bàiPoint: 100
Nhiệm vụ của bạn là với mỗi số ~k = 1, 2, \ldots, n~, đếm xem có bao nhiêu cách đặt ~2~ quân mã trên bàn cờ ~k \times k~ mà chúng không tấn công nhau.
Input
- Gồm một số nguyên dương ~n~ duy nhất (~2 \leq n \leq 10^4~).
Output
- In ra kết quả trên các dòng khác nhau.
Sample Test
Input:
8
Output:
0
6
28
96
252
550
1056
1848



