Một đêm nọ, một tên trộm nọ quyết định đột nhập vào một siêu thị nọ. Siêu thị có ~N~ mặt hàng, mặt hàng thứ ~i~ có trọng lượng ~A_i~, giá trị ~B_i~ và có thể coi một mặt hàng có vô hạn số lượng hàng. Tên trộm mang theo một cái túi chứa được trọng lượng tối đa ~W~. Hỏi tổng giá trị tối đa tên trộm có thể lấy được là bao nhiêu?

Input

• Dòng thứ nhất gồm hai số nguyên dương ~N~ và ~W~ (~1 \leq N, W \leq 10^3~).
• Trong ~N~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên dương ~A_i~ và ~B_i~ (~A_i, B_i \leq 10^3~).

Output

• In ra tổng giá trị lớn nhất có thể được lấy đi.

Sample Test

Input:

2 100
1 1
50 49

Output:

100

Ở đất nước Omega người ta chỉ tiêu tiền xu. Có ~N~ loại tiền xu, loại thứ ~i~ có mệnh giá là ~A_i~ đồng. Một người khách du lịch đến Omega du lịch với số tiền ~M~ đồng. Ông ta muốn đổi số tiền đó ra tiền xu Omega để tiện tiêu dùng.

Bạn hãy giúp ông ta tìm ~1~ cách đổi tiền để số đồng tiền đổi được là ít nhất (cho túi tiền đỡ nặng khi đi đây đi đó).

Input

• Dòng thứ nhất gồm hai số nguyên dương ~N~ và ~M~ (~N \leq 100, M \leq 10^3~).
• Dòng thứ hai gồm ~N~ số nguyên dương ~A_1, A_2, \ldots, A_N~ khác nhau (~A_i \leq 10^3, A_1 = 1~).

Output

• In ra số lượng đồng tiền ít nhất để đổi ~M~ đồng thành xu Omega.

Sample Test

Input:

3 8
1 4 5

Output:

2

Một ma trận ~A~ kích thước ~m \times n~ có thể biểu diễn dưới dạng:

$$ \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \ldots\\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix} $$

Phép nhân giữa ma trận ~A~ kích thước ~m \times n~ và ma trận ~B~ kích thước ~n \times p~ là một ma trận ~C~ có kích thước ~m \times p~, với

$$ \begin{equation} C_{ij} = \sum^{n}_{k=1} A_{ik} \times B_{kj} \space (1 \leq i \leq m, 1 \leq j \leq p) \end{equation} $$

Như vậy, nhân ~A~ với ~B~ ta cần thực hiện tổng cộng ~m \times n \times p~ phép toán. Để dễ hiểu hơn ta có thể minh hoạ phép nhân ma trận như sau:

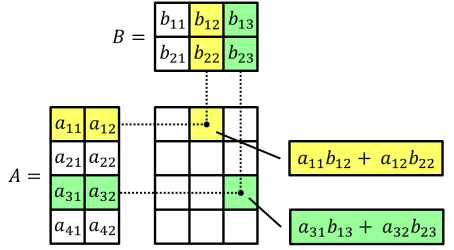
Ma trận không có tính giao hoán, tuy nhiên vẫn có tính kết hợp, tức là ~(A \times B) \times C~ = ~A \times (B \times C)~. Số lượng phép tính cần thực hiện cho ~2~ trình tự tính là khác nhau.

Cho ~N~ ma trận ~A_1, A_2, \ldots, A_N~, ma trận ~i~ có kích thước ~d_{i - 1} \times d_i~. Hãy xác định trình tự nhân ma trận ~A_1 \times A_2 \times \ldots \times A_N~ sao cho số phép nhân cần thực hiện là ít nhất.

Input

• Dòng thứ nhất gồm số nguyên dương ~N~ (~N \leq 100~).
• Dòng thứ hai gồm ~N + 1~ số nguyên dương ~d_0, d_1, d_2 \ldots, d_N~ (~d_i \leq 100~).

Output

• In ra số phép tính ít nhất cần để thực hiện biểu thức nhân ma trận.

Sample Test

Input:

4
40 20 30 10 30

Output:

26000

Note:

• Có 4 ma trận ~A_{40 \times 20}, B_{20 \times 30}, C_{30 \times 10}, D_{10 \times 30}~.
• Trinh tự nhân tối ưu: ~(A \times (B \times C)) \times D~.
• Số lượng phép tính: ~20 \times 30 \times 10 + 40 \times 20 \times 10 + 40 \times 10 \times 30 = 26000~.

Có ~n~ lọ hoa sắp thẳng hàng và ~k~ bó hoa được đánh số thứ tự từ nhỏ đến lớn. Cần cắm ~k~ bó hoa trên vào ~n~ lọ sao cho hoa có số thứ tự nhỏ phải đứng trước hoa có số thứ tự lớn. Giá trị thẩm mỹ tương ứng khi cắm bó hoa thứ ~i~ vào lọ thứ ~j~ là ~v_{i, j}~.

Hãy tìm ~1~ cách cắm sao cho tổng giá trị thẩm mỹ là lớn nhất. Chú ý rằng mỗi bó hoa chỉ được cắm vào ~1~ lọ và mỗi lọ cũng chỉ cắm được ~1~ bó hoa.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~k~ (~k \leq n~).
• ~k~ dòng tiếp theo, mỗi dòng gồm ~n~ số nguyên dương ~v_{k, 1}, v_{k, 2}, \ldots, v_{k, n}~ mô tả giá trị thẩm mỹ khi cắm bó hoa thứ ~k~ vào lần lượt lọ hoa thứ ~1, 2, \ldots, n~.
• Giá trị các số trong phần Input không vượt quá ~10^3~.

Output

• In ra tổng giá trị thẩm mỹ lớn nhất.

Sample Test

Input:

3 2
5 7 5
8 9 6

Output:

14

Có ~N~ phòng học chuyên đề và ~K~ nhóm học được đánh số thứ tự từ nhỏ đến lớn. Phòng thứ ~i~ có ~a_i~ ghế và nhóm thứ ~j~ có ~b_j~ học sinh. Thầy giáo cần xếp các nhóm trên vào các phòng học sao cho nhóm có số hiệu nhỏ được xếp vào phòng có số hiệu nhỏ, nhóm có số hiệu lớn phải được xếp vào phòng có số hiệu lớn. Với mỗi phòng được xếp, số học sinh phải bằng số ghế thừa, tức các ghế thừa phải được chuyển ra hết, nếu thiếu ghế thì lấy vào cho đủ ghế.

Hãy chọn ~1~ phương án bố trí sao cho tổng số lần chuyển ghế ra và vào là ít nhất.

Input

• Dòng thứ nhất chứa ~2~ số nguyên dương ~N~ và ~K~ (~K < N \leq 10^3~).
• Dòng thứ hai chứa ~N~ số nguyên dương ~a_1, a_2, \ldots, a_N~ (~a_i \leq 10^3~).
• Dòng thứ ba chứa ~K~ số nguyên dương ~b_1, b_2, \ldots, b_K~ (~b_i \leq 10^3~).

Output

• In ra tổng số lần chuyển ghế ít nhất.

Sample Test

Input:

10 2
4 7 9 6 1 10 1 4 3 6
3 1

Output:

1

Cho bảng ~A~ gồm ~M \times N~ ô được đánh số theo thứ tự từ trên xuống dưới, trái sang phải. Từ ô ~(i,j)~ có thể di chuyển sang ~3~ ô ~(i + 1, j), (i + 1,j – 1)~ và ~(i + 1,j + 1)~ (nếu ô đấy tồn tại). Hãy xác định một lộ trình đi, xuất phát từ ~1~ ô bất kì hàng ~1~ đến ~1~ ô bất kì hàng ~M~ sao cho tổng các ô đi qua là nhỏ nhất.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~M~ và ~N~.
• ~M~ dòng tiếp theo, mỗi dòng chứa ~N~ số nguyên dương mô tả bảng số.
• Giá trị các số trong phần Input đều không vuợt quá ~10^3~.

Output

• In ra tổng giá trị nhỏ nhất đạt được.

Sample Test

Input:

3 3
2 3 5
2 3 1
3 4 2

Output:

6

Note:

• Lộ trình đi: ~(1, 2) \rightarrow (2, 3) \rightarrow (3, 3)~.

Cho một bảng vuông ~n \times n~ ô, một số ô có thể có bẫy. Các ô được đánh thứ tự trên trên xuống dưới, từ trái sang phải.

Nhiệm vụ của bạn là tính số lượng cách đi từ ô trái trên (toạ độ ~(1, 1)~) đến ô phải dưới (toạ độ ~(n, n)~) mà không đi qua bẫy. Bạn chỉ có thể di chuyển sang phải hoặc xuống dưới.

Input

• Dòng đầu tiên chứa số nguyên dương ~n~ - kích thước bảng (~n \leq 1000~).
• ~n~ dòng tiếp theo, mỗi dòng chứa ~n~ kí tự mô tả bảng vuông:
  • . mô tả một ô trống (có thể đi qua);
  • * mô tả một ô có bẫy (không thể đi qua).

Output

• In ra số lượng đường đi, lấy phần dư khi chia cho ~10^9 + 7~.

Sample Test