odtrain1
Prime Factor 1
Nộp bàiPoint: 100
Cho số nguyên dương ~n~, hãy phân tích ~n~ dưới dạng thừa số nguyên tố.
https://www.facebook.com/nguyen.uc.huy.97646/
Input
- Gồm số nguyên dương ~n~.
Output
- In ra theo ví dụ.
Constraints
- ~1 \le n \le 10^{12}~.
Sample Input 1
12
Sample Output 1
2 2
3 1
Giải thích
~12 = 2^2 \times 3^1~
Sàng nguyên tố
Nộp bàiPoint: 100
Bạn có một số nguyên dương ~N~. Nhiệm vụ của bạn là xuất ra tất cả các số nguyên tố từ ~1~ tới ~N~.
Input
- Gồm một dòng duy nhất chứa số nguyên ~N~ (~N \leq 10^6)~.
Output
- Xuất ra tất cả các số nguyên tố từ ~1~ tới ~N~ trên cùng một dòng và cách nhau một dấu cách.
Sample Tests
Input
10
Output
2 3 5 7
Prime Factor 2
Nộp bàiPoint: 100
Cho ~q~ truy vấn, mỗi truy vấn gồm một số nguyên dương ~n~.
Với mỗi truy vấn, hãy phân tích ~n~ dưới dạng thừa số nguyên tố.
Input
- Dòng đầu gồm số nguyên dương ~q~ miêu tả số truy vấn.
- ~q~ dòng sau, mỗi dòng gồm số nguyên dương ~n~.
Output
- In ra theo ví dụ.
Constraints
- ~1 \leq q \leq 2 \times 10^5~.
- ~1 \le n \leq 10^6~.
Sample Input 1
3
12
24
9
Sample Output 1
2 2
3 1
2 3
3 1
3 2
Giải thích
~12 = 2^2 \times 3^1~
~24 = 2^3 \times 3^1~
~9 = 3^2 ~
TPrime
Nộp bàiPoint: 100
Chúng ta đã quá rõ việc một số nguyên tố (prime) là số nguyên dương lớn hơn ~1~ có duy nhất hai ước là ~1~ và chính nó. Để làm mới bài toán, hôm nay, ta sẽ định nghĩa một số TPrime là một số nguyên dương lớn hơn ~1~ gồm đúng ~3~ ước.
Cho ~n~ truy vấn, mỗi truy vấn là một số ~a~, hãy kiểm tra xem số này có phải là số TPrime hay không.
Input
- Dòng ~1~ ghi số nguyên dương ~n~ ~(1 \le n \le 3*10^5)~
- ~n~ dòng sau, mỗi dòng gồm một số nguyên dương ~a~ ~(1 \le a \le 10^{12})~ miêu tả truy vấn.
Output
- In ra ~n~ dòng, với mỗi truy vấn, nếu ~a~ là số TPrime thì in ra "YES", ngược lại in ra "NO".
Subtask
- Có ~20\%~ số test ứng với ~1 \le n \le 100, 1 \le a \le 10^4~
- Có ~30\%~ số test ứng với ~1 \le n,a \le 10^5~
- Có ~50\%~ số test còn lại không có giới hạn gì thêm.
Sample Input 1
3
4
6
7
Sample Output 1
YES
NO
NO
Lona Prime
Nộp bàiPoint: 100
Ngày mai lớp của ~Lona~ sẽ có buổi kiểm tra Tin học. ~Lona~ rất lo lắng vì đề thầy cho rất khó và hại não. Do đó để có thể được thêm điểm cộng cho bài kiếm tra này thì ~Lona~ đã quyết định sẽ xung phong giải bài tập về nhà.
Thầy giáo cho các bạn trong lớp một số nguyên dương ~n~ và yêu cầu đếm tất cả các số nguyên dương ~s~ thỏa mãn:
- ~s \le n~
- ~s = p^3 \times q^3~ với ~p~ và ~q~ là các số nguyên tố phân biệt.
Loay hoay mãi nhưng ~Lona~ vẫn chưa thể giải được nên đành nhờ các bạn giúp đỡ. Là một lập trình thiên tài, bạn hãy giúp đỡ ~Lona~ nhé.
Input
Dòng duy nhất nhập vào một số nguyên dương ~n~ ~(1 \le n \le 10^{18})~.
Output
In ra yêu cầu đề bài: số số nguyên dương ~s~ thỏa mãn.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~50~ | ~n \le 10 ^ 6~ |
| 2 | ~50~ | Không có điều kiện gì thêm |
Sample Input 1
1000
Sample Output 1
2
Notes
Có ~2~ số thỏa mãn đề bài:
- ~216 = 2^3 \times 3^3~
- ~1000 = 2^3 \times 5^3~
3 số nguyên tố
Nộp bàiPoint: 100
Cho số ~n~. Hãy tìm số ~k \le n~ lớn nhất sao cho ~k~ là tích của 3 số nguyên tố liên tiếp.
Input
- Gồm số tự nhiên ~n \le 10^{18}~.
Output
- Gồm duy nhất một số tự nhiên ~k~. Nếu không có số thỏa mãn in ra -1.
Sample Test
Input:
31
Output
30
SumLen
Nộp bàiPoint: 100
Cho một dãy ~a~ gồm ~n~ phần tử nguyên không âm.
Hãy đếm số đoạn con liên tiếp ~[l,r]~ của dãy ~a~ sao cho tổng của đoạn con đó bằng độ dài của đoạn, hay ~a_l + a_{l+1} + ... + a_r = r - l + 1~.
Input
- Dòng đầu tiên chứa số nguyên dương ~n~.
- Dòng thứ hai gồm ~n~ số nguyên không âm miêu tả dãy ~a~.
Output
- In ra số đoạn con thỏa mãn.
Điều kiện
- ~1 \le n \le 2*10^5~.
- ~0 \le a \le 9~.
Subtask
- ~50\%~ số điểm: ~n \le 1000~.
- ~50\%~ số điểm: ~n \le 2*10^5~.
Ví dụ
Input 1:
3
1 2 0
Output 1:
3
Input 2:
5
1 1 0 1 1
Output 2:
6
MS
Nộp bàiPoint: 100
Cho một dãy ~a~ gồm ~n~ phần tử nguyên.
Hãy tìm đoạn con liên tiếp có tổng lớn nhất của dãy
Input
- Dòng đầu tiên chứa số nguyên dương ~n~.
- Dòng thứ hai gồm ~n~ số nguyên miêu tả dãy ~a~.
Output
- In ra giá trị thỏa mãn.
Điều kiện
- ~1 \le n \le 2*10^5~.
- ~|a| \le 10^6~.
Subtask
- ~50\%~ số điểm: ~n \le 1000~.
- ~50\%~ số điểm: ~n \le 2*10^5~.
Ví dụ
Input 1:
4
3 -2 4 -1
Output 1:
5
qsum
Nộp bàiPoint: 100
Cho dãy ~a~ nguyên dương gồm ~n~ phần tử. Ta định nghĩa hàm ~f(l,r)~ như sau: ~f(l,r) = 1\times a[l] + 2\times a[l+1] + 3\times a[l+2] + ... (r-l+1)\times a[r]~.
Có ~q~ truy vấn, mỗi truy vấn gồm hai số ~l~, ~r~ với ~1 \le l \le r \le n~. Với mỗi truy vấn, hãy in ra ~f(l,r)~.
Input
- Dòng đầu gồm 2 số nguyên dương ~n~ và ~q~. ~(1 \le n, q \le 10^5)~
- Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy ~a~. ~(1 \le a[i] \le 10^5)~.
- ~q~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên dương ~l~, ~r~ miêu tả các truy vấn.
Ouput
- In ra ~q~ dòng, mỗi dòng là kết quả của một truy vấn tương ứng.
Subtask
- Subtask ~1~: ~n,q \le 2 \times 10^3~ ~(30\%)~
- Subtask ~2~: Trong tất cả các truy vấn, ~l=1~.
- Subtask ~3~: Không giới hạn gì thêm ~(40\%)~.
Sample Test
Input
4 3
1
2
3
4
1 2
2 3
1 4
Output
5
8
30
Tổng đọan con
Nộp bàiPoint: 100
Cho một mảng gồm ~n~ số nguyên, nhiệm vụ của bạn là đếm số lượng đoạn con có tổng ~x~.
Input
- Dòng đầu vào đầu tiên có hai số nguyên ~n~ và ~x~: kích thước của mảng và tổng ~x~.
- Dòng tiếp theo có ~n~ số nguyên ~a_1, a_2, \ldots, a_n~: nội dung của mảng.
Output
- In một số nguyên: số lượng đoạn con được yêu cầu.
Constraints
- ~1 \le n \le 2 \cdot 10^5~
- ~-10^9 \le x, a_i \le 10^9~
Sample Tests
Input
5 7
2 -1 3 5 -2
Output
2
Cập nhật 1
Nộp bàiPoint: 100
Cho dãy ~a~ gồm ~n~ phần tử ~a_1, a_2, ..., a_n~. Thực hiện ~m~ thao tác, mỗi thao tác gồm ba số ~(l, r, x)~ có ý nghĩa: tăng các phần tử có chỉ số từ ~l~ đến ~r~ thêm ~x~ đơn vị.
Hãy in ra dãy ~a~ sau khi thực hiện ~m~ thao tác trên.
Input
- Dòng đầu tiên chứa hai số nguyên ~n, m \ (1 \le n, m\le 10^5)~.
- Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, ..., a_n \ (|a_i| \le 10^5, 1\le i\le n)~.
- ~m~ dòng sau, mỗi dòng chứa ba số nguyên ~l_i, r_i, x_i \ (1\le l_i \le r_i \le n, |x_i| \le 10^5, 1\le i\le m)~.
Output
Dãy ~a~ sau khi thực hiện hết ~m~ thao tác.
Ví dụ
Input
5 3
1 -2 3 -4 5
1 2 1
2 4 -2
1 5 3
Output
5 0 4 -3 8
Cập nhật 2
Nộp bàiPoint: 100
Cho dãy ~a~ gồm ~n~ phần tử có giá trị bằng ~0~ và thực hiện ~m~ thao tác, mỗi thao tác gồm ba số ~(l, r, x)~ có ý nghĩa: tăng các phần tử có chỉ số từ ~l~ đến ~r~ thêm ~x~ đơn vị.
Hãy đếm số phần tử chia hết cho ~k~ trong dãy ~a~ sau khi thực hiện ~m~ thao tác trên.
Input
- Dòng đầu tiên chứa ba số nguyên ~n, m, k \ (1\le n\le 10^{18}, 1\le m\le 10^5, 1\le k\le 100)~.
- ~m~ dòng sau, mỗi dòng chứa ba số nguyên ~l_i, r_i, x_i \ (1\le l_i \le r_i \le n, |x_i| \le 10^9, 1\le i\le m)~.
Output
Kết quả gồm một số nguyên dương là số phần tử chia hết cho ~k~ của dãy ~a~ mới.
Ví dụ
Input
5 2 3
2 4 1
3 5 2
Output
3
UpdOp
Nộp bàiPoint: 100
Cho một dãy ~a~ gồm ~n~ phần tử nguyên không âm và ~q~ thao tác, thao tác thứ ~i~ có dạng ~(l_i,r_i,d_i)~, nghĩa là tăng giá trị của các phần tử trong mảng ~a~ từ vị trí ~l_i~ tới ~r_i~ thêm ~d_i~ đơn vị.
Bạn cần thực hiện ~k~ truy vấn, truy vấn thứ ~i~ có dạng ~(x_i,y_i)~, có nghĩa là thực hiện các thao tác ~x_i,x_{i} + 1,...,y_i~.
Hãy in ra giá trị của các phần tử trong mảng ~a~ sau khi thực hiện ~k~ truy vấn.
Input
- Dòng đầu tiên chứa ~3~ số nguyên dương ~n,q,k~.
- Dòng thứ hai gồm ~n~ số nguyên không âm miêu tả dãy ~a~.
- ~q~ dòng sau, dòng thứ ~i~ gồm ~3~ số nguyên dương ~l_i,r_i,d_i~ miêu tả thao tác thứ ~i~.
- ~k~ dòng sau, dòng thứ ~i~ gồm ~2~ số nguyên dương ~x_i,y_i~ miêu tả truy vấn thứ ~i~.
Output
- Gồm một dòng in ra ~n~ số, số thứ ~i~ là giá trị của phần tử ~a_i~ sau khi thực hiện ~k~ truy vấn.
Điều kiện
- ~1 \le n, q, k \le 10^5~.
- ~0 \le a_i,d_i \le 10^5~.
Subtask
- ~50\%~ số điểm: ~n \le 1000~.
- ~50\%~ số điểm: ~n \le 10^5~.
Ví dụ
Input 1:
3 3 3
1 2 3
1 2 1
1 3 2
2 3 4
1 2
1 3
2 3
Output 1:
9 18 17
Input 2:
4 3 6
1 2 3 4
1 2 1
2 3 2
3 4 4
1 2
1 3
2 3
1 2
1 3
2 3
Output 2:
5 18 31 20
Điểm chung
Nộp bàiPoint: 100
Trên trục số ~Ox~, cho ~𝑁~ đoạn thẳng, mỗi đoạn thẳng được xác định bởi hai điểm đầu và cuối là hai số nguyên. Một điểm ~𝑀~ được gọi là nằm trong đoạn thẳng ~𝐴𝐵~ nếu ~𝐴 ≤ 𝑀 ≤ 𝐵~.
Yêu cầu: Đếm xem có bao nhiêu điểm có toạ độ nguyên nằm trong đúng ~𝐾~ đoạn thẳng.
Dữ liệu nhập vào từ file văn bản DC.INP:
- Dòng đầu tiên gồm hai số nguyên ~𝑁~ và ~𝐾~ ~(1 ≤ 𝐾 ≤ 𝑁 ≤ 10^5);~
- ~𝑁~ dòng sau, mỗi dòng gồm hai số nguyên ~𝑎, 𝑏~ mô tả hai điểm đầu và cuối của đoạn thẳng ~(1 ≤ 𝑎 ≤ 𝑏 ≤ 10^{18})~.
Kết quả ghi ra file văn bản DC.OUT:
Một số nguyên duy nhất là số lượng điểm có toạ độ nguyên nằm trong đúng ~𝐾~ đoạn thẳng.
Ràng buộc
- Có ~50\%~ số test ứng với ~50\%~ số điểm của bài thoả mãn: ~𝑎, 𝑏 ≤ 10^3;~
- ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thoả mãn: ~𝐾 = 𝑁;~
- ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.
Ví dụ
Input
3 2
1 5
2 8
3 7
Output
3
Giải thích: Toạ độ của ~3~ điểm nằm trong đúng ~2~ đoạn thẳng là: ~2, 6, 7~.
- Điểm có toạ độ ~2~ nằm trong ~2~ đoạn thẳng: đầu tiên và thứ hai.
- Điểm có toạ độ ~6, 7~ nằm trong ~2~ đoạn thẳng: thứ hai và thứ ba.
Input
3 1
1 5
2 8
3 7
Output
2
Giải thích: Toạ độ của ~2~ điểm nằm trong đúng ~1~ đoạn thẳng là: ~1, 8~.
- Điểm có toạ độ ~1~ chỉ nằm trong đoạn thẳng đầu tiên.
- Điểm có toạ độ ~8~ chỉ nằm trong đoạn thẳng thứ ba.
Input
3 3
1 5
2 8
3 7
Output
3
Giải thích: Toạ độ của ~3~ điểm nằm trong cả ~3~ đoạn thẳng là: ~3,4,5~.
Cập nhật 3
Nộp bàiPoint: 100
Cho dãy ~a~ gồm ~n~ phần tử xếp thành một vòng tròn có giá trị bằng ~0~ và thực hiện ~m~ thao tác, mỗi thao tác gồm hai số ~(l, r)~ có ý nghĩa: tăng các phần tử có chỉ số từ ~l~ đến ~r~ thêm ~1~ đơn vị.
Sau khi thực hiện xong ~m~ thao tác, hãy tìm phần tử lớn nhất trong dãy và đưa ra số lần xuất hiện của phần tử đó trong dãy ~a~ mới.
Input
- Dòng đầu tiên chứa hai số nguyên ~n, m \ (1\le n\le 10^{18}, 1\le m\le 10^5)~.
- ~m~ dòng sau, mỗi dòng chứa hai số nguyên ~l_i, r_i \ (1\le l_i, r_i \le n, 1\le i\le m)~.
Output
Kết quả gồm hai số nguyên dương là đáp án của bài toán trên.
Ví dụ
Input
5 2
1 5
4 2
Output
2 4
Giải thích
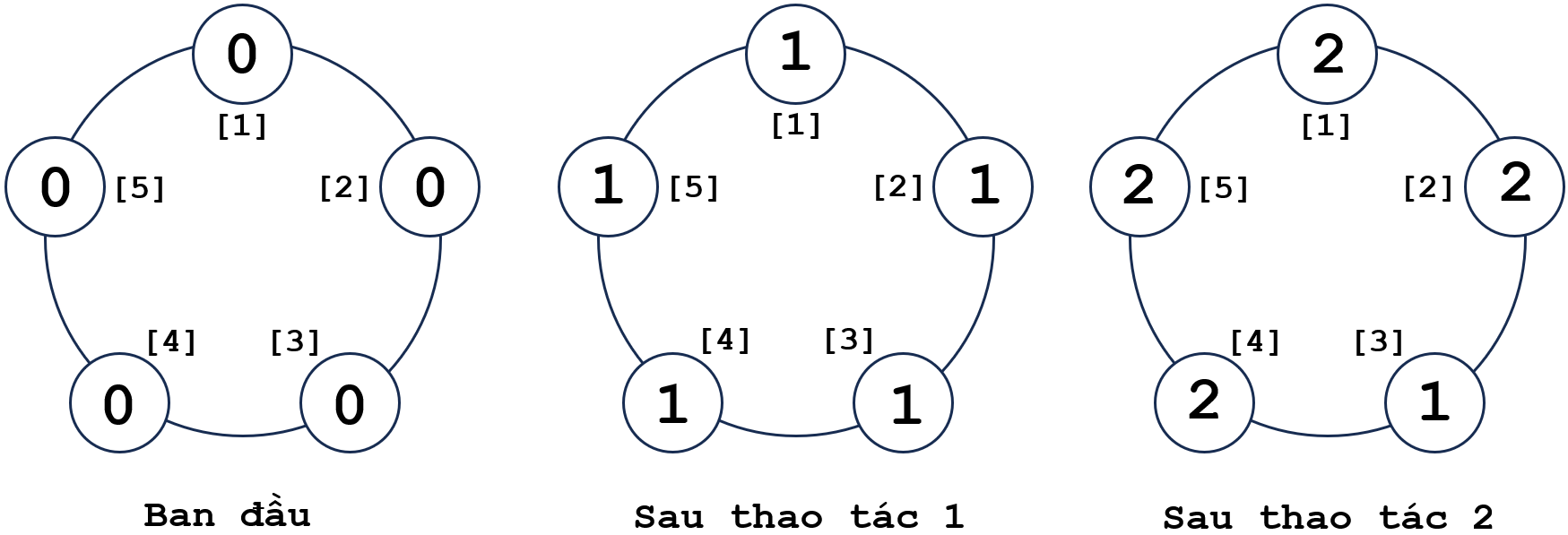
Cập nhật bậc thang
Nộp bàiPoint: 100
Cho mảng ~A~ gồm ~n~ số nguyên, ban đầu tất cả các phần tử đều bằng ~0~. Bạn được cho ~q~ truy vấn có dạng ~(l, r)~: với mỗi phần tử ~A_i~ mà ~l \le i \le r~, thêm vào nó một giá trị ~i - l + 1~.
Yêu cầu: ghi ra mảng ~A~ sau khi thực hiện tất cả các truy vấn.
Input
- Dòng đầu tiên gồm ~2~ số nguyên dương ~n, q~ (~1 \le n, q \le 10^5~).
- ~q~ dòng tiếp theo mỗi dòng gồm 2 số nguyên ~l, r~ (~1 \le l, r \le n~).
Output
- In ra mảng ~A~ sau tất cả truy vấn.
Sample Test
Input:
4 2
1 3
2 4
Output:
1 3 5 3
Chú ý: Sau truy vấn đầu tiên, ~A~ trở thành ~{1, 2, 3, 0}~.
Tính tổng 2
Nộp bàiPoint: 100
Cho bảng ~a~ có ~n~ dòng, ~m~ cột, giao của dòng thứ ~i~ và cột thứ ~j~ là ô ~(i, j)~, có giá trị là ~a_{i, j}~.
Cho ~q~ truy vấn, mỗi truy vấn gồm ~4~ số ~(x, y, u, v)~. Với mỗi truy vấn, hãy tính tổng của các ô nằm trong bảng con của ~a~ có góc bên trái phía trên là ô ~(x, y)~ và góc bên phải phía dưới là ô ~(u, v)~.
Input
- Dòng đầu tiên chứa hai số nguyên ~n, m, q \ (1\le n, m \le 1000; q\le 10^6)~.
- ~n~ dòng sau, dòng thứ ~i~ chứa ~m~ số nguyên ~a_{i, j}~ ~(|a_{i, j}| \le 10^5, 1\le i\le n, 1\le j\le m)~.
- ~q~ dòng sau, mỗi dòng chứa bốn số nguyên ~x_i, y_i, u_i, v_i \ (1\le x_i \le u_i \le n, 1\le y_i \le v_i \le m, 1\le i\le q)~.
Output
Kết quả gồm ~q~ dòng, dòng thứ ~i~ là kết quả của truy vấn thứ ~i~ ~(1\le i\le q)~.
Ví dụ
Input
3 3 4
1 2 3
3 2 1
1 2 3
1 1 3 3
2 2 2 3
1 2 3 2
2 1 3 2
Output
18
3
6
8
Đếm k
Nộp bàiPoint: 100
Cho ma trận kích thước ~n \times m~ và một số nguyên ~k~.
Cho ~q~ truy vấn, mỗi truy vấn gồm ~4~ số ~(x, y, u, v)~. Với mỗi truy vấn, hãy đếm số phần tử bằng ~k~ nằm trong bảng con có góc bên trái phía trên là ô ~(x, y)~ và góc bên phải phía dưới là ô ~(u, v)~.
Input
- Dòng đầu chứa ~3~ số nguyên ~n, m~ và ~k~ (~2 \leq n, m \leq 1000, 1 \leq k \leq 10^9~).
- ~n~ dòng tiếp theo, mỗi dòng chứa ~m~ số nguyên ~a_{i,j}~ phân cách bởi dấu cách (~0 \leq a_{i,j} \leq 1000~).
- Dòng thứ ~n+1~ chứa số nguyên ~q~ (~1 \leq q \leq 10^5~) - số lượng truy vấn.
- ~q~ dòng sau, mỗi dòng chứa bốn số nguyên ~x_i, y_i, u_i, v_i \ (1\le x_i \le u_i \le n, 1\le y_i \le v_i \le m, 1\le i\le q)~.
Output
- Kết quả gồm ~q~ dòng, dòng thứ ~i~ in ra kết quả của truy vấn ~i~.
Sample Test
Input:
3 4 2
1 5 3 2
3 2 1 5
1 4 3 3
2
1 1 2 2
2 3 3 4
Output:
1
0
Ma trận k
Nộp bàiPoint: 100
Cho ma trận kích thước ~n \times m~. Hãy tìm ma trận con vuông ~k \times k~ có tổng lớn nhất.
Input
- Dòng đầu chứa ~3~ số nguyên ~n, m~ và ~k~ (~2 \leq k \leq n,m \leq 1000~) - kích thước ma trận và ma trận con.
- ~n~ dòng tiếp theo, mỗi dòng chứa ~m~ số nguyên ~a_{i,j}~ phân cách bởi dấu cách (~0 \leq a_{i,j} \leq 1000~).
Output
- In ra tổng của ma trận con ~k \times k~ có tổng lớn nhất.
Sample Test
Input:
3 4 2
1 1 1 1
3 2 1 1
5 1 1 1
Output:
11
Đếm tam giác
Nộp bàiPoint: 100
Bạn có ~N~ que có độ dài khác nhau và cần tạo một số tam giác từ các que này. Một tam giác hợp lệ nếu diện tích của nó lớn hơn ~0~. Nhiệm vụ của bạn là tìm số cách có thể tạo một tam giác hợp lệ bằng cách sử dụng các que.
Input
- Dòng đầu tiên chứa một số nguyên ~N~ (~3 \leq N \leq 2000~) - số lượng que.
- Dòng tiếp theo chứa ~N~ số nguyên biểu thị độ dài của các que. Bạn có thể giả sử rằng các độ dài là khác nhau và mỗi độ dài nằm trong khoảng [~1,10^9~].
Output
- In ra tổng số cách có thể tạo ra một tam giác hợp lệ.
Sample Test
Input:
4
100 211 212 121
Output:
4
Tam giác nhọn
Nộp bàiPoint: 100
Mít có các que tính có nhiều độ dài và màu sắc. Hôm nay học về hình tam giác nhọn, Mít đã nghĩ ra một bài toán rất độc đáo có liên quan tới tam giác nhọn và các que tính của mình. Mít chia các que tính thành ~N~ bộ, các que tính trong cùng một bộ thì có độ dài bằng nhau nhưng có màu khác nhau. Độ dài của các que tính trong hai bộ bất kì là khác nhau. Mít đố các bạn đếm xem có bao nhiêu tam giác nhọn khác nhau có thể được tạo ra từ ~N~ bộ que tính đó. Chú ý: mỗi cạnh của tam giác được chọn từ một bộ que tính khác nhau tức là sẽ không có tam giác cân và hai tam giác nhọn được gọi là giống nhau khi các cặp cạnh tương ứng bằng nhau và cùng màu, ngược lại là khác nhau.
Yêu cầu: Cho độ dài và số lượng các que tính của ~N~ bộ que tính, hãy lập trình đếm số lượng tam giác nhọn khác nhau có thể tạo ra.
Dữ liệu vào từ tệp văn bản TRIACU.INP:
- Dòng đầu tiên gồm một số nguyên dương ~N~ ~(N ≤ 2000)~ là số bộ que tính;
- ~N~ dòng sau, dòng thứ ~i~ chứa hai số nguyên dương ~L, C~ mô tả độ dài và số lượng que tính của bộ thứ ~i~ ~(1 ≤ i ≤ N~; ~\ L ≤ 10^6~; ~\ C ≤ 10^3)~.
Kết quả ghi ra tệp văn bản TRIACU.OUT:
Một số nguyên duy nhất là số lượng tam giác nhọn khác nhau.
Ràng buộc
- Có ~50\%~ số test ứng với ~N ≤ 200~;
- ~50\%~ số test còn lại không có điều kiện gì thêm.
Ví dụ
Input
4
3 3
4 1
5 2
6 2
Output
4
Giải thích
Có ~4~ tam giác nhọn có thể tạo ra từ bộ que tính thứ ~2, 3, 4~.
Số thứ K
Nộp bàiPoint: 100
Cho ~2~ mảng ~a~ và ~b~ đều gồm ~n~ số nguyên dương và một số nguyên dương ~k~. Mảng số nguyên ~c~ gồm ~n^2~ phần tử được xây dựng bằng cách với mỗi cặp ~i,j~ thỏa mãn ~1 \le i,j \le n~, ta gán giá trị ~c_{(i-1)*n+j} = a_i + b_j~.
Sắp xếp mảng ~c~ lại theo thứ tự không giảm, hãy in ra số thứ ~k~ trong dãy ~c~ mới.
Input
- Dòng đầu gồm ~2~ số nguyên dương ~n~ và ~k~.
- Dòng tiếp theo gồm ~n~ số nguyên dương mô tả dãy ~a~.
- Dòng cuối cùng gồm ~n~ số nguyên dương mô tả dãy ~b~.
Output
- In ra kết quả của bài toán.
Constraints
- ~1 \le n \le 10^5~, ~1 \le k \le n^2~.
- ~1 \le a_i,b_i \le 10^9~.
Subtask
- ~50\%~ số điểm có ~n \le 1000~.
- ~50\%~ còn lại không có giới hạn gì thêm.
Sample Input 1
5 10
4 2 6 4 8
7 3 1 9 5
Sample Output 1
9
Bnumber
Nộp bàiPoint: 100
Số đẹp được định nghĩa là một số nguyên dương và chia hết cho một trong hai số: ~3~ hoặc ~5~.
Ví dụ về dãy các số đẹp: ~3, 5, 6, 9, 10, 12, 15, 18, 20,...~
Hãy tìm số đẹp thứ ~k~.
Input
- Gồm một dòng chứa số nguyên dương ~k~.
Output
- In ra kết quả của bài toán.
Giới hạn:
- Subtask 1 (~50\%~ số điểm): ~k \le 10^6~
- Subtask 2 (~50\%~ số điểm): ~k \le 10^{12}~
Sample Input 1
2
Sample Output 1
5
Sample Input 2
10
Sample Output 2
21
Gộp mảng
Nộp bàiPoint: 100
Cho hai mảng ~A, B~ gồm các phần tử nguyên không giảm. Hãy ghép chúng lại thành một mảng số nguyên không giảm.
Lưu ý, các bạn cần giải bài toán này với độ phức tạp là ~O(n)~
Input
- Dòng đầu chứa số nguyên ~n~.
- Dòng thứ hai chứa ~n~ số nguyên ~A_i~.
- Dòng thứ ba chứa ~n~ số nguyên ~B_i~.
Output
- In ra ~n \times 2~ số nguyên là mảng kết quả.
Điều kiện
- ~1 \le n \le 10^5~.
- ~1 \le A_i, B_i \le 10^9~
Ví dụ
Input:
3
1 3 4
1 2 3
Output:
1 1 2 3 3 4
sort1
Nộp bàiPoint: 100
Cho mảng ~A~ gồm ~N~ số nguyên dương. Sắp xếp mảng không giảm.
Hướng dẫn sort:

Input
- Dòng đầu tiên chứa duy nhất số nguyên ~N~ (~1 \leq N \leq 5000~).
- Dòng tiếp theo chứa ~N~ số nguyên dương ~A_i~ (~A_i \leq 10^9~).
Output
- Sắp xếp mảng ban đầu không giảm.
Sample Test
| Input | Output |
|---|---|
| 5 5 4 2 6 3 |
2 3 4 5 6 |


