Số nguyên dương ~d~ được gọi là ước của số nguyên dương ~N~ nếu ~N~ chia hết cho ~d~. Ví dụ: các ước của ~9~ là ~1, 3~ và ~9;~ các ước của ~10~ là ~1, 2, 5~ và ~10~.

Yêu cầu: Cho hai số nguyên dương ~L~ và ~R~ ~(L ≤ R)~. Hãy tính tổng của tất cả các số nguyên dương là ước của ít nhất một số trong đoạn từ ~L~ tới ~R~ ~(~bao gồm cả ~L~ và ~R)~.

Dữ liệu vào từ tệp văn bản SUMDIV.INP:

Gồm một dòng chứa hai số nguyên dương ~L~ và ~R~ ~(1 ≤ L ≤ R ≤ 10^9).~

Kết quả ghi ra tệp văn bản SUMDIV.OUT:

Một số nguyên duy nhất là tổng của tất cả các số nguyên dương là ước của ít nhất một số trong đoạn từ ~L~ tới ~R~.

Ràng buộc

• Có ~20\%~ số test ứng với ~R ≤ 1000~;
• ~25\%~ số test khác ứng với ~R - L ≤ 1000~;
• ~25\%~ số test khác ứng với ~R ≤ 10^6~;
• ~30\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input

9 12

Output

63

Giải thích

Các số là ước của ít nhất một số trong đoạn ~[9, 12]~ là: ~1, 2, 3, 4, 5, 6, 9, 10, 11~ và ~12~ ~(7~ và ~8~ không nằm trong danh sách này vì cả ~9, 10, 11~ và ~12~ đều không chia hết cho ~7~ hoặc ~8)~.

Ta có ~1 + 2 + 3 + 4 + 5 + 6 + 9 + 10 + 11 + 12 = 63~.

Input

7 7

Output

8

Giải thích

Các số là ước của ~7~ là ~1~ và ~7~. Ta có ~1 + 7 = 8~.

Mít có các que tính có nhiều độ dài và màu sắc. Hôm nay học về hình tam giác nhọn, Mít đã nghĩ ra một bài toán rất độc đáo có liên quan tới tam giác nhọn và các que tính của mình. Mít chia các que tính thành ~N~ bộ, các que tính trong cùng một bộ thì có độ dài bằng nhau nhưng có màu khác nhau. Độ dài của các que tính trong hai bộ bất kì là khác nhau. Mít đố các bạn đếm xem có bao nhiêu tam giác nhọn khác nhau có thể được tạo ra từ ~N~ bộ que tính đó. Chú ý: mỗi cạnh của tam giác được chọn từ một bộ que tính khác nhau tức là sẽ không có tam giác cân và hai tam giác nhọn được gọi là giống nhau khi các cặp cạnh tương ứng bằng nhau và cùng màu, ngược lại là khác nhau.

Yêu cầu: Cho độ dài và số lượng các que tính của ~N~ bộ que tính, hãy lập trình đếm số lượng tam giác nhọn khác nhau có thể tạo ra.

Dữ liệu vào từ tệp văn bản TRIACU.INP:

• Dòng đầu tiên gồm một số nguyên dương ~N~ ~(N ≤ 2000)~ là số bộ que tính;
• ~N~ dòng sau, dòng thứ ~i~ chứa hai số nguyên dương ~L, C~ mô tả độ dài và số lượng que tính của bộ thứ ~i~ ~(1 ≤ i ≤ N~; ~\ L ≤ 10^6~; ~\ C ≤ 10^3)~.

Kết quả ghi ra tệp văn bản TRIACU.OUT:

Một số nguyên duy nhất là số lượng tam giác nhọn khác nhau.

Ràng buộc

• Có ~50\%~ số test ứng với ~N ≤ 200~;
• ~50\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input

4
3 3
4 1
5 2
6 2

Output

4

Giải thích

Có ~4~ tam giác nhọn có thể tạo ra từ bộ que tính thứ ~2, 3, 4~.

Giá trị nén của một số nguyên dương ~X~ kí hiệu là ~N(X)~, được tính bằng tích các chữ số của nó. Ví dụ: ~N(123) = 6~, ~N(90) = 0~.

Yêu cầu: Cho hai số nguyên dương ~L, R~ ~(L ≤ R)~, tìm giá trị nén lớn nhất của các số nguyên không bé hơn ~L~ và không lớn hơn ~R~.

Dữ liệu vào từ tệp văn bản COMNUM.INP:

Gồm một dòng duy nhất chứa hai số nguyên dương ~L, R~.

Kết quả ghi ra tệp văn bản COMNUM.OUT:

Một số nguyên duy nhất là giá trị nén lớn nhất của các số thỏa mãn điều kiện đề bài.

Ràng buộc

• Có ~20\%~ số test ứng với ~L ≤ R ≤ 10^6~;
• ~30\%~ số test khác ứng với ~L ≤ R ≤ 10^{18}~;
• ~20\%~ số test khác ứng với ~L ≤ R ≤ 10^{100}~;
• ~30\%~ số test còn lại ứng với ~L ≤ R ≤ 10^{100000}~.

Ví dụ

Input

15 24

Output

9

Trong thành phố có ~N~ trạm tiếp sóng. Trên bản thiết kế xây dựng, trạm thứ ~i~ có tọa độ là ~(x_i, y_i)~. Giữa hai trạm ~i~ và ~j~, chi phí để liên kết hai trạm này với nhau là ~\min(|x_i − x_j|, |y_i − y_j|)~. Lãnh đạo thành phố muốn liên kết toàn bộ các trạm tiếp sóng với nhau (hai trạm được gọi là có liên kết với nhau khi chúng có liên kết trực tiếp với nhau hoặc liên kết qua một số trạm trung gian khác).

Yêu cầu: Hãy giúp lãnh đạo thành phố tính tổng chi phí nhỏ nhất để liên kết toàn bộ ~N~ trạm tiếp sóng.

Dữ liệu vào từ tệp văn bản BTS.INP:

• Dòng đầu tiên ghi số nguyên ~N~ ~(2 ≤ N ≤ 10^5)~ là số trạm tiếp sóng;
• ~N~ dòng tiếp theo, dòng thứ ~i~ ghi hai số nguyên ~x_i~ và ~y_i~ ~(1 ≤ i ≤ N~; ~\ 1 ≤ x_i ≤ 10^9~; ~\ 1 ≤ y_i ≤ 10^9)~ là tọa độ của trạm tiếp sóng thứ ~i~.

Kết quả ghi ra tệp văn bản BTS.OUT:

Một số nguyên duy nhất là tổng chi phí nhỏ nhất để liên kết các trạm tiếp sóng trên.

Ràng buộc

• Có ~50\%~ số test ứng với ~N ≤ 10^3~;
• ~50\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input

5
4 9
9 5
0 2
7 1
3 4

Output

5

Giải thích

• Liên kết giữa trạm ~2~ và ~4~ với chi phí ~2~.
• Liên kết giữa trạm ~3~ và ~4~ với chi phí ~1~.
• Liên kết giữa trạm ~2~ và ~5~ với chi phí ~1~.
• Liên kết giữa trạm ~1~ và ~5~ với chi phí ~1~.

Tổng chi phí sẽ là: ~2 + 1 + 1 + 1 = 5~.

Trên hệ trục tọa độ vuông góc ~Oxy~, cho tọa độ ~N~ điểm trong đó không có ba điểm nào thẳng hàng.

Yêu cầu: Tìm hai điểm trong ~N~ điểm để đường thẳng chứa hai điểm đó chia ~N-2~ điểm còn lại thành hai phần sao cho tổng số điểm của mỗi phần chênh lệnh nhau không quá ~1~.

Dữ liệu vào từ tệp văn bản DIVPOINT.INP:

• Dòng đầu tiên gồm một số nguyên dương ~N~ ~(N ≤ 10^5)~ là số lượng điểm;
• ~N~ dòng sau, mỗi dòng chứa hai số nguyên ~x, y~ là toạ độ của một điểm ~(|x| ≤ 10^9~; ~\ |y| ≤ 10^9)~.

Kết quả ghi ra tệp văn bản DIVPOINT.OUT:

Một dòng gồm bốn số nguyên là toạ độ của hai điểm thoả mãn. Có thể có nhiều kết quả, ghi ra một kết quả bất kì.

Ràng buộc

• Có ~30\%~ số test ứng với ~N ≤ 100~;
• ~30\%~ số test khác ứng với ~N ≤ 5000~;
• ~40\%~ số test còn lại ứng với ~N ≤ 10^5~.

Ví dụ

Input

4
0 0
0 1
1 1
1 0

Output

0 0 1 1

Trên trục ~Ox~, cho ~N~ đoạn thẳng được đánh số từ ~1~ tới ~N~, đoạn thẳng thứ ~i~ ~(1 ≤ i ≤ N)~ nối điểm có tọa độ nguyên ~x = a_i~ và điểm có tọa độ nguyên ~x = b_i~ ~(a_i < b_i)~. Một điểm được gọi là thuộc đoạn thẳng thứ ~i~ nếu tọa độ của nó nằm trong đoạn ~[a_i, b_i]~.

Yêu cầu: Cho biết ~N~ đoạn thẳng và một số nguyên dương ~K~. Hãy viết một chương trình trả lời ~Q~ truy vấn. Ở truy vấn thứ ~j~ ~(1 ≤ j ≤ Q)~, khi cho biết hai số nguyên ~c_j~ và ~d_j~, bạn cần xác định giá trị ~L~ lớn nhất sao cho tồn tại hai số nguyên ~u, v~ thỏa mãn:

• ~c_j ≤ u < v ≤ d_j~ và ~v − u = L~;
• Tồn tại không quá ~K~ đoạn thẳng trong số ~N~ đoạn thẳng được cho sao cho mọi điểm ~x~ có tọa độ nguyên trong đoạn ~[u, v]~ đều thuộc ít nhất một trong các đoạn thẳng đó.

Nếu không tồn tại ~u, v~ nào thì ~L = 0~.

Dữ liệu vào từ tệp văn bản SEGMENT.INP:

• Dòng đầu tiên chứa ba số nguyên dương ~N,Q,K~ ~(1 ≤ K ≤ N ≤ 10^5, \ 1 ≤ Q ≤ 10^5)~;
• ~N~ dòng tiếp theo, dòng thứ ~i~ ~(1 ≤ i ≤ N)~ chứa hai số nguyên ~a_i~ và ~b_i~ ~(0 ≤ a_i < b_i ≤ 10^9)~;
• ~Q~ dòng cuối cùng, dòng thứ ~j~ ~(1 ≤ j ≤ Q)~ chứa hai số nguyên ~c_j~ và ~d_j~ ~(0 ≤ c_j < d_j ≤ 10^9)~.

Kết quả ghi ra tệp văn bản SEGMENT.OUT:

Gồm ~Q~ dòng, dòng thứ ~j~ ~(1 ≤ j ≤ Q)~ là giá trị ~L~ lớn nhất cho truy vấn thứ ~j~.

Ràng buộc

• Có ~20\%~ số test ứng với ~K = 1~; ~\ N,Q ≤ 2000~;
• ~20\%~ số test khác ứng với ~K = 1~;
• ~20\%~ số test khác ứng với ~K = 2~;
• ~20\%~ số test khác ứng với ~K ≤ 30~;
• ~20\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input

3 4 1
6 8
1 5
4 6
1 10
2 6
4 7
5 9

Output

4
3
2
2

Giải thích

• Truy vấn ~1~: chọn ~[u, v] = [1, 5]~.
• Truy vấn ~2~: chọn ~[u, v] = [2, 5]~.
• Truy vấn ~3~: chọn ~[u, v] = [4, 6]~.
• Truy vấn ~4~: chọn ~[u, v] = [6, 8]~.

Input

4 3 2
2 5
6 8
9 11
8 10
1 8
6 11
8 11

Output

3
4
3

Giải thích

• Truy vấn ~1~: chọn ~[u, v] = [2, 5]~.
• Truy vấn ~2~: chọn ~[u, v] = [6, 10]~.
• Truy vấn ~3~: chọn ~[u, v] = [8, 11]~.

Trong giờ sinh hoạt lớp, cô giáo tổ chức cho các bạn học sinh chơi một trò chơi "Tô màu dãy ô vuông". Ban đầu, cô giáo chuẩn bị một dãy các ô vuông xếp cạnh nhau và được đánh số từ ~1~ đến ~N~ và được tô toàn bộ màu có số hiệu là ~0~. Trò chơi diễn ra trong ~M~ lượt chơi, mỗi lượt cô gọi một học sinh bất kì lên tô màu dải ô vuông: học sinh sẽ nghĩ ra ba số nguyên dương ~L, R, C~ ~(L ≤ R)~ và thực hiện tô màu có số hiệu ~C~ từ ô ~L~ đến ô ~R~ (màu của ô vuông sẽ là màu của người tô sau). Kết thúc ~M~ lượt chơi rất hăng say, được một dãy ô vuông rất đẹp, cô giáo bảo các bạn ghi lại ba số ~L, R, C~ mà các bạn nghĩ ra ở lượt chơi của mình và cô giáo đánh số lại các lượt chơi từ ~1~ đến ~M~. Sau đó, cô giáo đố các bạn một câu hỏi rất hóc búa: từ danh sách ghi thông tin tô màu của các bạn học sinh, hãy đưa ra thứ tự các lượt tô màu để từ dãy ô vuông ban đầu thu được dãy ô vuông khi trò chơi kết thúc.

Yêu cầu: Hãy giúp các bạn học sinh sắp xếp lại thứ tự các lượt tô màu.

Dữ liệu vào từ tệp văn bản COLOR.INP:

• Dòng đầu tiên chứa hai số nguyên dương ~N~ và ~M~ ~(1 ≤ N, M ≤ 5 \times 10^5)~ là số ô vuông và số lượt tô màu~;~
• ~M~ dòng sau, mỗi dòng thứ ~i~ chứa ba số nguyên ~L_i, R_i, C_i~ ~(1 ≤ i ≤ M;~ ~\ 1 ≤ L_i ≤ R_i ≤ N;~ ~\ 1 ≤ C_i ≤ 5 \times 10^5)~ mô tả dòng thứ ~i~ ở danh sách ghi thông tin một lượt lượt tô màu~;~
• Dòng cuối cùng chứa ~N~ số nguyên là số hiệu màu của từng ô vuông sau khi các bạn đã tô màu.

Kết quả ghi ra tệp văn bản COLOR.OUT:

Một dòng gồm ~M~ số nguyên là thứ tự tô màu để thu được dãy ô vuông khi trò chơi kết thúc. Có thể có bạn ghi nhầm thông tin lượt tô màu của mình nên không tìm được cách chọn thì in ra ~−1~. Nếu có nhiều cách chọn thì in ra cách bất kì.

Ràng buộc

• Có ~20\%~ số test ứng với ~1 ≤ N, M ≤ 9;~
• ~20\%~ số test khác ứng với ~1 ≤ N, M ≤ 5000~ và màu của mỗi lần tô là khác nhau~;~
• ~20\%~ số test khác ứng với ~1 ≤ N, M ≤ 5 \times 10^5~ và màu của mỗi lần tô là khác nhau~;~
• ~20\%~ số test khác ứng với ~1 ≤ N, M ≤ 5000;~
• ~10\%~ số test khác ứng với ~1 ≤ N, M ≤ 5 \times 10^5~ và ~1 ≤ C_i ≤ 5;~
• ~10\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input

6 5
3 5 5
1 1 6
1 3 2
1 4 7
4 6 6
6 2 5 5 5 6

Output

4 5 3 1 2

Số nguyên dương ~N~ là chia hết cho ~9~ khi và chỉ khi tổng các chữ số của nó chia hết cho ~9~.

Yêu cầu: Cho số nguyên dương ~N~. Hãy đổi một chữ số trong ~𝑁~ sao cho số mới được tạo ra có giá trị nhỏ nhất và chia hết cho ~9~. Số mới được tạo ra có thể có chữ số ~0~ ở đầu tiên.

Dữ liệu nhập vào từ file văn bản CH9.INP:

• Dòng đầu tiên chứa ~T~ là số test dữ liệu của bài toán ~(T \le 15);~
• ~T~ dòng tiếp theo, mỗi dòng chứa một số nguyên dương ~N~.

Tổng số lượng chữ số ở mọi test không quá ~10^6~.

Kết quả ghi ra file văn bản CH9.OUT:

Gồm ~𝑇~ dòng, mỗi dòng chứa một số nguyên dương tương ứng là kết quả theo yêu cầu.

Ràng buộc:

• Có ~50\%~ số test tương ứng với ~50\%~ số điểm của bài thoả mãn: ~T=1;~
• ~50\%~ số test còn lại ứng với ~50\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

3
34125
5441
22221

Output

34128
0441
22221

Trong một cơ quan, có ~𝑁~ yêu cầu sử dụng phòng họp trực tuyến. Cơ quan đã đăng kí với cấp trên đường truyền ưu tiên theo ~𝑀~ mốc thời gian được đánh số từ ~1~ đến ~M~. Mỗi yêu cầu đăng kí sử dụng phòng họp trong các mốc thời gian liên tiếp từ ~𝐿~ đến ~𝑅~ ~(1 ≤ 𝐿 ≤ 𝑅 ≤ 𝑀)~. Để tiện cho việc sắp xếp và phục vụ các phòng họp, cần biết mỗi yêu cầu xung đột với bao nhiêu yêu cầu khác (hai yêu cầu gọi là xung đột với nhau nếu có chung ít nhất một mốc thời gian).

Yêu cầu: Cho biết ~𝑁~ yêu cầu sử dụng phòng họp. Với mỗi yêu cầu, hãy tính số lượng yêu cầu xung đột với nó.

Dữ liệu nhập vào từ file văn bản XPH.INP:

• Dòng đầu chứa số hai nguyên ~𝑁,𝑀~ ~(1 ≤ 𝑁 ≤ 2 \times 10^5; \ 1 ≤ 𝑀 ≤ 10^9)~ là số lượng yêu cầu và số lượng mốc thời gian~;~
• ~N~ dòng tiếp theo, dòng thứ ~𝑖~ chứa hai số nguyên ~𝐿_i,𝑅_i \ (1 ≤ 𝐿_i ≤ 𝑅_i ≤ 𝑀; \ 1 ≤ 𝑖 ≤ 𝑁)~ là mốc thời gian bắt đầu và kết thúc của yêu cầu thứ ~𝑖~.

Kết quả ghi ra file văn bản XPH.OUT:

Gồm ~𝑁~ dòng, dòng thứ ~𝑖~ mô tả số lượng yêu cầu xung đột với yêu cầu thứ ~𝑖~ ~(1 ≤ 𝑖 ≤ 𝑁)~.

Ràng buộc

• Có ~25\%~ số test ứng với ~25\%~ số điểm của bài thoả mãn: ~𝑁, 𝑀 ≤ 400;~
• ~25\%~ số test khác ứng với ~25\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 2000;~
• ~25\%~ số test khác ứng với ~25\%~ số điểm của bài thoả mãn: ~𝑀 ≤ 4 \times 10^5;~
• ~25\%~ số test còn lại ứng với ~25\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

5 7
1 2
2 5
3 5
7 7
4 6

Output

1
3
2
0
2

Lớp A1 tổ chức liên hoan cuối năm và đã đặt các món ăn cho từng học sinh trong lớp từ một nhà hàng. Cụ thể, lớp có ~𝑁~ học sinh, nhà hàng cung cấp ~𝑀~ món ăn khác nhau với giá tương ứng ~c_1, c_2, … , c_m~. Hiện tại, mỗi học sinh đã chọn xong cho mình một món ăn. Tuy nhiên, các bạn trong lớp nghĩ rằng có càng nhiều món ăn khác nhau trong buổi liên hoan thì cả lớp sẽ càng vui hơn.

Sau khi cân nhắc, các bạn muốn buổi liên hoan có ít nhất ~𝐾~ món ăn khác nhau. Nhà hàng cho phép học sinh đổi món ăn của họ bằng một món ăn khác đắt tiền hơn và phải trả thêm khoản chênh lệch chi phí giữa hai món ăn.

Yêu cầu: Hãy giúp lớp A1 tính toán tổng chi phí nhỏ nhất để có ít nhất ~K~ món ăn khác nhau trong buổi liên hoan, hoặc thông báo là không thể thực hiện được điều này.

Dữ liệu nhập vào từ file văn bản CMA.INP:

• Dòng đầu chứa ba số nguyên ~𝑁, 𝑀, 𝐾~ ~(1 ≤ 𝑁, 𝑀 ≤ 2 \times 10^5; \ 1 ≤ 𝐾 ≤ 𝑁);~
• Dòng thứ hai chứa ~𝑁~ số nguyên ~a_1, 𝑎_2, … , 𝑎_N~ là các món ăn mà các bạn trong lớp đã chọn ~(1 ≤ 𝑎_i ≤ 𝑀; \ 1 ≤ 𝑖 ≤ 𝑁);~
• Dòng thứ ba chứa ~𝑀~ số nguyên ~𝑐_1, 𝑐_2, … , 𝑐_M~ là giá của các món ăn ~(1 ≤ 𝑐_j ≤ 10^9; \ 1 ≤ 𝑗 ≤ 𝑀).~

Kết quả ghi ra file văn bản CMA.OUT:

Tổng chi phí nhỏ nhất cần để đổi các món ăn của các bạn trong lớp để thoả mãn yêu cầu, hoặc in ra ~-1~ nếu không có cách nào để có được ~𝐾~ món ăn khác nhau.

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑎_1 = 𝑎_2 = ⋯ = 𝑎_N;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝐾 = 𝑁;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁, 𝑀 ≤ 15;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑐_i = 𝑖;~
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

3 4 3
1 1 2
1 2 3 4

Output

2

Trong một trò chơi, có một robot di chuyển trên một bản đồ dạng cây gồm ~𝑁~ ngọn núi và ~𝑁 − 1~ con đường nối các ngọn núi. Mỗi ngọn núi có ~𝐾~ kho báu và mỗi con đường nối hai ngọn núi đều có ~2~ kho báu. Quy tắc di chuyển của robot như sau:

• Robot chọn một ngọn núi để xuất phát~;~
• Tại mỗi lượt di chuyển qua một ngọn núi hoặc một con đường, robot khai thác để lấy một kho báu và di chuyển tiếp~;~
• Robot có thể di chuyển từ ngọn núi ~𝑢~ đến ~𝑣~ nếu thoả mãn cả hai điều kiện: con đường nối ngọn núi ~u~ đến ngọn núi ~𝑣~ còn lại ít nhất một kho báu và ngọn núi ~𝑣~ còn lại ít nhất một kho báu. Nếu không còn kho báu, ngọn núi và con đường sẽ bị phá huỷ, robot không thể di chuyển đến.

Yêu cầu: Em hãy tính xem robot có thể đi qua nhiều nhất bao nhiêu con đường.

Dữ liệu nhập vào từ file văn bản TKB.INP:

• Dòng đầu tiên chứa hai số nguyên dương ~𝑁, 𝐾~ ~(𝑁 ≤ 10^5; \ 𝐾 ≤ 10^9);~
• ~𝑁 − 1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~𝑢, 𝑣~ ~(1 ≤ 𝑢, 𝑣 ≤ 𝑁)~ mô tả con đường nối hai ngọn núi.

Kết quả ghi ra file văn bản TKB.OUT:

In ra một số nguyên là số lượng con đường nhiều nhất mà robot đi qua.

Ràng buộc

• Có ~30\%~ số test ứng với ~30\%~ số điểm của bài thoả mãn: ~𝐾 = 1;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 20;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 300; \ 𝐾 = 2;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 1000;~
• ~10\%~ số test còn lại ứng với ~10\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

7 1
1 2
2 3
4 2
5 1
6 1
6 7

Output

4

Giải thích

Robot có thể di chuyển theo thứ tự các ngọn núi: ~3 − 2 − 1 − 6 − 7~. Robot đi qua 4 con đường.

Input

4 3
1 2
2 4
2 3

Output

6

Giải thích

Robot có thể di chuyển theo thứ tự các ngọn núi: ~1 − 2 − 4 − 2 − 3 − 2 − 1~. Robot đi qua ~6~ con đường.

Cho dãy số nguyên dương ~𝐴~ có ~𝑁~ phần tử ~𝑎_1, 𝑎_2, … , 𝑎_N~. Có ~𝑄~ truy vấn có dạng ~𝐿, 𝑅, 𝐾~ với ý nghĩa như sau:

• Xét dãy con ~𝐵~ là dãy con của ~𝐴~ gồm các phần tử liên tiếp từ vị trí ~𝐿~ đến vị trí ~𝑅~ : ~𝑎_L, 𝑎_{L+1}, … , a_R~ ~(1 ≤ 𝐿 ≤ 𝑅 ≤ 𝑁)~, ta xây dựng dãy số ~𝐶~ bằng cách coi ~𝐶~ là tập hợp tất cả các dãy con liên tiếp của ~B~. Ví dụ: dãy ~𝐵 = \{1, 2, 1\}~ các dãy con của ~B~ là ~\{1\}, \{2\}, \{1\}, \{1,2\}, \{2,1\}, \{1,2,1\}~ ta sẽ có dãy ~𝐶 = \{1, 2, 1, 1, 2, 2,1, 1,~~ 2, 1\};~
• Sắp xếp dãy ~𝐶~ theo thứ tự không giảm và đưa ra phần tử thứ ~𝐾~. Ví dụ: với dãy ~𝐶~ trên ta sắp xếp thành ~\{1, 1, 1, 1, 1, 1, 2, 2, 2, 2\}~ và phần tử thứ ~8~ là ~2~.

Yêu cầu: Cho dãy số ~𝐴~ và ~𝑄~ truy vấn như trên, hãy đưa ra kết quả phần tử thứ ~𝐾~ của dãy số ~𝐶~ tương ứng trong mỗi truy vấn.

Dữ liệu nhập vào từ file văn bản DLT.INP:

• Dòng đầu tiên gồm hai số nguyên dương ~𝑁~ và ~𝑄~ ~(1 ≤ 𝑁, 𝑄 ≤ 5 \times 10^5)~ là số phần tử của dãy số ~𝐴~ và số lượng truy vấn~;~
• Dòng thứ hai gồm ~𝑁~ số nguyên dương ~𝑎_1, 𝑎_2, … , 𝑎_N~ ~(1 ≤ 𝑎_i ≤ 5 \times 10^5; \ 1 ≤ 𝑖 ≤ 𝑁);~
• ~𝑄~ dòng sau, mỗi dòng chứa ba số ~𝐿, 𝑅, 𝐾~ ~(1 ≤ 𝐿 ≤ 𝑅 ≤ 𝑁)~ mô tả truy vấn.

Dữ liệu đảm bảo đúng đắn, luôn có kết quả.

Kết quả ghi ra file văn bản DLT.OUT:

~𝑄~ dòng là kết quả tương ứng của mỗi truy vấn.

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁, 𝑄 ≤ 100;~
• ~10\%~ số test khác ứng với ~10\%~ số điểm của bài thoả mãn: ~𝑁, 𝑎_i ≤ 100;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁, 𝑄, 𝑎_i ≤ 5000;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁, 𝑄 ≤ 10^5; 𝑎_i ≤ 100;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁, 𝑄, 𝑎_i ≤ 10^5;~
• ~10\%~ số test còn lại ứng với ~10\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

5 2
1 2 1 3 2
1 3 8
1 4 18

Output

2
3

Cho ba số nguyên không âm ~N, K, X~. Với dãy số ~0, 1, 2, 3, ..., N~ người ta sắp xếp lại dãy số đó theo quy tắc:

• Đầu tiên là bộ các số chia ~K~ dư ~X~;
• Tiếp theo là bộ các số chia ~K~ dư ~X+1~;
• ~...~
• Tiếp theo là bộ các số chia ~K~ dư ~K-1~;
• Tiếp theo là bộ các số chia hết cho ~K~;
• Tiếp theo là bộ các số chia ~K~ dư ~1~;
• ~...~
• Cuối cùng là bộ các số chia ~K~ dư ~X-1~.

Trong mỗi bộ số có cùng tính chia hết, các số được sắp xếp giảm dần.

Ví dụ: ~N=10, K=4, X=2~.

• Ta có: bộ các số chia ~4~ dư ~2~ là ~10, 6, 2~; bộ các số chia ~4~ dư ~3~ là ~7, 3~; bộ các số chia hết cho ~4~ là ~8, 4, 0~; bộ các số chia ~4~ dư ~1~ là ~9, 5, 1~;
• Dãy số sau khi sắp xếp là: ~10, 6, 2, 7, 3, 8, 4, 0, 9, 5, 1~.

Yêu cầu: Cho ~Q~ truy vấn, mỗi truy vấn chứa ba số nguyên không âm ~N, K, X~ và số nguyên dương ~D~. Tìm số thứ ~D~ của dãy số sau khi sắp xếp.

Dữ liệu vào từ tệp văn bản DCH.INP:

• Dòng đầu tiên chứa số nguyên dương ~Q~ không vượt quá ~10^6~ là số lượng truy vấn;
• ~Q~ dòng tiếp theo: Mỗi dòng mô tả một truy vấn gồm bốn số ~N, K, X, D~ ~(0 \le X \lt K \lt N \le 10^{18}, D \le N + 1)~.

Dữ liệu ghi ra tệp văn bản DCH.OUT:

Gồm ~Q~ dòng, mỗi dòng chứa kết quả của một truy vấn.

Ví dụ

Input

2
10 4 2 5
10 3 0 6

Output

3
7

Giải thích

Trong truy vấn thứ hai: ~N=10, K=3, X=0~

• Dãy số sau khi sắp xếp là: ~9, 6, 3, 0, 7, 4, 1, 8, 5, 2~;
• Số thứ ~6~ là ~7~.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm thoả mãn: ~Q, N \le 10^3~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~X=0, Q\le 10^5~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho một xâu ~S~ chỉ gồm các chữ cái tiếng Anh in thường. Các chữ cái a, b, ..., z lần lượt được đánh số thứ tự là ~1, 2, ..., 26~. Trọng số của một xâu được định nghĩa là tổng các giá trị tuyệt đối của hiệu số thứ tự giữa các ký tự trong xâu với ký tự đầu tiên của xâu đó.

Ví dụ, với xâu cadc, trọng số của xâu là: ~|'c'-'c'|+|'a'-'c'|+|'d'-'c'|+|'c'-'c'|=|3-3|+|1-3|+|4-3|+|3-3|=0+2+1+0=3~.

Yêu cầu: Hãy tìm một xâu con gồm các ký tự liên tiếp thuộc ~S~ có trọng số lớn nhất và có ký tự đầu trùng với ký tự cuối.

Dữ liệu vào từ tệp văn bản TSX.INP:

Gồm một xâu ký tự có độ dài là ~N~ ~(N \le 10^6)~.

Dữ liệu ghi ra tệp văn bản TSX.OUT:

Một số nguyên là trọng số lớn nhất của xâu con thoả mãn.

Ví dụ

Input

bcacadbac

Output

8

Giải thích

Chọn xâu con cacadbac.

Input

abcaczc

Output

25

Giải thích

Chọn xâu con caczc.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm thoả mãn: ~N\le 10^2~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~N\le 10^4~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho một dãy ~A~ gồm ~N~ số nguyên ~A_1, A_2, ..., A_N~ (các phần tử có giá trị từ ~1~ đến ~9~). Gọi ~S[L~...~R]~ là số nguyên được ghép bởi các số từ vị trí ~L~ đến vị trí ~R~ trong dãy ~A~, theo thứ tự từ trái sang phải. Ví dụ: với dãy ~A=[2,6,5,7,4]~ thì ~S[2~...~5]~ là số ~6574~.

Một số nguyên không âm được gọi là may mắn nếu như trong biểu diễn thập phân của số đó không chứa số ~13~. Ví dụ: các số may mắn là ~6, 12, 31, 103, ...~; các số không may mắn là ~13, 5713, 321321, ...~

Yêu cầu: Bạn cần thực hiện ~Q~ yêu cầu thuộc một trong hai loại sau:

• Loại ~1~: Đưa ra số lượng các số may mắn không vượt quá ~S[L~...~R]~;
• Loại ~2~: Thay giá trị phần tử thứ ~i~ bằng giá trị ~X~.

Dữ liệu vào từ tệp văn bản SMM.INP:

• Dòng đầu tiên chứa hai số nguyên dương ~N, Q~ ~(N, Q\le 2 \times 10^5)~;
• Dòng thứ hai gồm ~N~ số nguyên ~A_1, A_2, ..., A_N~ viết liền nhau ~(1 \le A_i \le 9; 1\le i \le N)~;
• ~Q~ dòng tiếp theo, mỗi dòng chứa một yêu cầu thuộc một trong hai dạng sau:
  • 1 L R: Mô tả yêu cầu ghi ra số lượng số may mắn không vượt quá ~S[L~...~R]~ ~(1 \le L \le R \le N)~ sau khi chia dư cho ~10^9+7~;
  • 2 i X: Mô tả yêu cầu thay giá trị phần tử thứ ~i~ bằng giá trị ~X~ ~(1 \le i \le N; 1 \le X \le 9)~.

Dữ liệu ghi ra tệp văn bản SMM.OUT:

Với mỗi yêu cầu loại ~1~, ghi ra kết quả trên một dòng.

Ví dụ

Input

6 3
849613
1 1 2
2 3 4
1 4 4

Output

84
7

Giải thích

Với yêu cầu đầu tiên, các số may mắn không vượt quá ~84~ là ~0, 1, 2, ..., 12, 14, 15, ..., 84~.

Với yêu cầu thứ hai, dãy ~A~ là ~844613~.

Với yêu cầu thứ ba, các số may mắn không vượt quá ~6~ là ~0, 1, 2, ..., 5, 6~.

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm thoả mãn: ~N\le 6; Q=1~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N\le 6~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N\le 100~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~Q\le 2000~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

TR là một hệ thống trao đổi dữ liệu trực tiếp giữa các máy tính đang được thử nghiệm tại trường ~X~. Trường có ~N~ máy tính được đánh số từ ~1~ đến ~N~. Các máy tính đều sử dụng hệ thống TR và được kết nối với nhau theo đồ thị dạng cây.

Ban đầu, hệ thống có một tệp dữ liệu đang được lưu trữ bởi một hoặc hai máy tính. Trường muốn truyền tệp này đến tất cả các máy tính khác trong hệ thống. Cơ chế truyền dữ liệu của hệ thống TR như sau: cứ một phút, mỗi máy tính trong hệ thống chỉ có thể truyền dữ liệu đến duy nhất một máy tính khác được kết nối trực tiếp với nó.

Yêu cầu: Cho số hiệu của các máy tính đang lưu trữ tệp dữ liệu ở thời điểm ban đầu. Hãy tính thời gian tối thiểu để tất cả các máy tính trong hệ thống nhận được tệp dữ liệu.

Dữ liệu vào từ tệp văn bản TDL.INP:

• Dòng đầu tiên chứa số nguyên ~N~ ~(1 \lt N \le 10^5)~ là số lượng máy tính;
• ~N-1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên khác nhau ~x~ và ~y~ ~(1 \le x, y \le N)~ mô tả số hiệu của hai máy tính được kết nối trực tiếp;
• Dòng tiếp theo chứa số ~M~ ~(1\le M\le 2)~ là số lượng máy tính đang lưu trữ tệp dữ liệu ở thời điểm ban đầu;
• Dòng tiếp theo chứa ~M~ số nguyên dương mô tả số hiệu của các máy tính đang lưu trữ tệp dữ liệu ở thời điểm ban đầu;

Dữ liệu ghi ra tệp văn bản TDL.OUT:

Gồm một số nguyên là thời gian tối thiểu hoàn thành công việc.

Ví dụ

Input

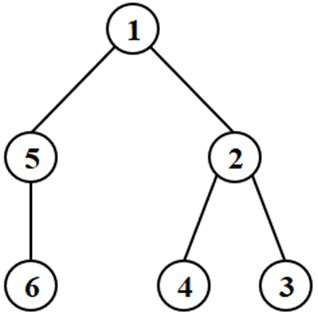
6
1 2
2 3
2 4
1 5
5 6
1

Output

3

Giải thích

Ban đầu máy ~1~ lưu trữ tệp dữ liệu.

Phút thứ ~1~: máy ~2~ nhận được tệp dữ liệu.

Phút thứ ~2~: máy ~3~ và ~5~ nhận được tệp dữ liệu.

Phút thứ ~3~: máy ~4~ và ~6~ nhận được tệp dữ liệu.

Input

6
1 2
2 3
2 4
1 5
5 6
2
1 2

Output

2

Giải thích

Ban đầu máy ~1~ và ~2~ lưu trữ tệp dữ liệu.

Phút thứ ~2~: máy ~3~ và ~5~ nhận được tệp dữ liệu.

Phút thứ ~3~: máy ~4~ và ~6~ nhận được tệp dữ liệu.

Minh hoạ

Ràng buộc

• Có ~25\%~ số test ứng với ~25\%~ số điểm có ~N\le 20~;
• ~25\%~ số test khác ứng với ~25\%~ số điểm có ~M=1~;
• ~25\%~ số test khác ứng với ~25\%~ số điểm có ~M=2; N\le 1000~;
• ~25\%~ số test còn lại ứng với ~25\%~ số điểm không có ràng buộc gì thêm.

Cho số nguyên dương ~N~. Hãy tìm ra dãy số thoả mãn:

• Số lượng các phần tử lớn hơn ~2~, tất cả phần tử của dãy là số nguyên dương;
• Dãy số là dãy tăng dần vè chênh lệch giữa hai phần tử liên tiếp bằng nhau;
• Tổng tất cả các phần tử của dãy số là ~N~;
• Nếu có nhiều dãy có tổng bằng ~N~, tìm ra dãy có số lượng phần tử lớn nhất;
• Nếu có nhiều hơn một dãy thoả mãn, chọn dãy có phần tử đầu tiên là bé nhất.

Dữ liệu vào từ tệp văn bản DCD.INP:

Một dòng duy nhất chứa số nguyên dương ~N~ ~(N \le 10^9)~.

Dữ liệu ghi ra tệp văn bản DCH.OUT:

Gồm một dòng là dãy số thoả mãn. Nếu không có dãy số thoả mãn, ghi ra ~-1~.

Ví dụ

Input

12

Output

1 4 7

Giải thích

Dãy ~2, 4, 6~ hoặc ~3, 4, 5~ cũng có tổng là ~12~ và số lượng phần tử là ~3~. Nhưng dãy số ~1, 4, 7~ là dãy có phần tử đầu tiên bé nhất.

Input

20

Output

2 3 4 5 6

Giải thích

Dãy ~2, 4, 6, 8~ cũng có tổng là ~20~ và số lượng phần tử là ~4~. Nhưng dãy số ~2, 3, 4, 5, 6~ là dãy có số lượng phần tử lớn hơn.

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm thoả mãn: ~N \le 10^3~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~N \le 10^5~;
• ~30\%~ số test còn lại ứng với ~30\%~ số điểm không có ràng buộc gì thêm.

Cho một tập ~S~ gồm ~N~ xâu ký tự ~S_1, S_2, ..., S_N~. Mỗi xâu trong tập ~S~ chỉ chứa các chữ cái tiếng Anh in thường. Với xâu ~S_i~ ~(1\le i\le N)~, chọn ra một xâu con không rỗng gồm các ký tự liên tiếp, gọi xâu con đó là ~T_i~. Sau đó, nối các xâu ~T_1, T_2, ..., T_N~ theo thứ tự từ trái qua phải tạo thành xâu ~P~.

Yêu cầu: Cho số nguyên dương ~K~, hãy tìm xâu ~P~ có độ dài đúng bằng ~K~ và có thứ tự từ điển nhỏ nhất.

Dữ liệu vào từ tệp văn bản NX.INP:

• Dòng đầu tiên chứa hai số nguyên ~N~ và ~K~ lần lượt là số lượng xâu trong tập ~S~ và độ dài xâu ~P~.
• ~N~ dòng tiếp theo, dòng thứ ~i~ ~(1\le i\le N)~ chứa xâu ký tự ~S_i~;

Dữ liệu đảm bảo ~1\le N\le K\le \sum^N_{i=1}|S_i|\le 4000~ với ~|S_i|~ là độ dài của xâu ~S_i~.

Dữ liệu ghi ra tệp văn bản NX.OUT:

Gồm một dòng là xâu ~P~ cần tìm.

Ví dụ

Input

2 3
aen
bbb

Output

abb

Giải thích

Chọn ra xâu con a của xâu aen.

Chọn ra xâu con bb của xâu bbb.

Input

2 3
bb
adh

Output

bad

Giải thích

Chọn ra xâu con b của xâu bb.

Chọn ra xâu con ad của xâu adh.

Ràng buộc

• Có ~30\%~ số test ứng với ~30\%~ số điểm thoả mãn: ~N=2; \ |S_1|, |S_2| \le 100~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~1\le N\le 50; \ |S_1|=|S_i|\le 10~ ~(1\le i \le N)~;
• ~40\%~ số test còn lại ứng với ~40\%~ số điểm không có ràng buộc gì thêm.

Cho ~N~ đoạn thẳng song song với trục ~Ox~, các đoạn thẳng được đánh số từ ~1~ đến ~N~. Đoạn thẳng thứ ~i~ ~(1\le i\le N)~ được xác định bởi điểm đầu và điểm cuối lần lượt là hai số nguyên dương ~l_i, r_i~. Hai đoạn thẳng ~i, j~ ~(1\le i, j\le N)~ được gọi là giao nhau khi: ~(r_i-l_i)+(r_j-l_j)\ge \max(r_i, r_j) - \min(l_i, l_j)~.

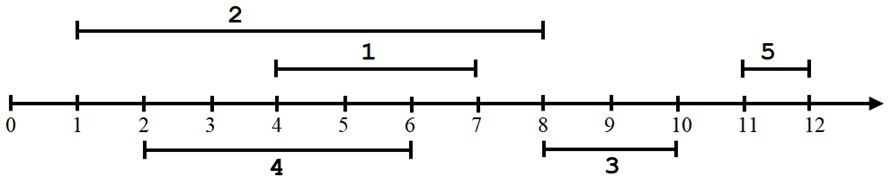
Ví dụ: như hình vẽ dưới, đoạn thẳng thứ ~1~ và ~4~, đoạn thẳng thứ ~2~ và ~3~, ... được gọi là giao nhau; đoạn thẳng thứ ~2~ và ~5~, đoạn thẳng thứ ~1~ và ~3~, ... không được gọi là giao nhau.

Yêu cầu: Hãy chọn ra hai tập đoạn thẳng ~S_1~ (có số lượng phần tử là ~x~) và ~S_2~ (có số lượng phần tử là ~y~) thoả mãn:

• Mỗi đoạn thẳng trong ~N~ đoạn thẳng thuộc tối đa một tập;
• Các đoạn thẳng trong cùng một tập đôi một giao nhau;
• ~x\ge y~ và ~y~ lớn nhất.

Dữ liệu vào từ tệp văn bản CT.INP:

• Dòng đầu chứa số nguyên dương ~N~ ~(2\le N\le 5 \times 10^5)~ là số lượng đoạn thẳng;
• ~N~ dòng tiếp theo, dòng thứ ~i~ ~(1\le i\le N)~ chứa hai số ~l_i, r_i~ ~(1\le l_i\le r_i\le 10^9)~ mô tả điểm đầu và điểm cuối của đoạn thẳng thứ ~i~.

Dữ liệu ghi ra tệp văn bản CT.OUT:

Ghi ra giá trị ~y~ thoả mãn.

Ví dụ

Input

5
4 7
1 8
8 10
2 6
11 12

Output

2

Giải thích

Có thể có nhiều cách lựa chọn ra hai tập.

Nếu chọn tập ~S_1~ gồm ~3~ đoạn thẳng thứ ~1, 2~ và ~4~; tập ~S_2~ gồm ~1~ đoạn thẳng thứ ~3~ hoặc ~5~; cách này có ~x=3, y=1~.

Nếu chọn tập ~S_1~ gồm ~2~ đoạn thẳng thứ ~1~ và ~4~; tập ~S_2~ gồm ~2~ đoạn thẳng thứ ~2~ và ~3~; cách này có ~x=2, y=2~.

Ràng buộc

• Có ~25\%~ số test ứng với ~25\%~ số điểm thoả mãn: ~N\le 500~;
• ~25\%~ số test khác ứng với ~25\%~ số điểm thoả mãn: ~N\le 5000~;
• ~25\%~ số test khác ứng với ~25\%~ số điểm thoả mãn: ~N\le 10^5~;
• ~25\%~ số test còn lại ứng với ~25\%~ số điểm không có ràng buộc gì thêm.