Cho ba số thực ~a~, ~b~, ~c~. Xác định xem ~a~, ~b~, ~c~ có thể là độ dài ba cạnh của một tam giác vuông hay không. Nếu không xác định xem ~a~, ~b~, ~c~ có là độ dài ba cạnh của một tam giác hay không.

Tổng độ dài 2 cạnh bất kì luôn lớn hơn độ dài cạnh còn lại.

Xét tam giác ABC vuông tại A, ta luôn có:

Input

Gồm 3 dòng, mỗi dòng chứa một số thực với độ lớn không vượt quá ~5 \times 10^3~ tương ứng với ba số ~a~, ~b~, ~c~.

Output

• In ra VUONG nếu ba số ~a~, ~b~, ~c~ là độ dài ba cạnh của một tam giác vuông.
• In ra KHONG nếu ba số ~a~, ~b~, ~c~ không là độ dài ba cạnh của một tam giác.
• In ra CO nếu hai điều trên cùng không thoả mãn.

Sample Test 1

Input:

3
5
4

Output:

VUONG

Sample Test 2

Input:

3
5
6

Output:

CO

Sample Test 3

Input:

2
3
6

Output:

KHONG

Cho hệ trục tọa độ ~Oxy~ có hai đường thẳng ~(D): y=ax+b~ và ~(\Delta) : y'=a'x+b'~.

Yêu cầu: Hãy xác định xem hai đường thẳng ~(D)~ và ~(\Delta)~ song song, cắt nhau hay trùng nhau.

Input

• Dòng đầu tiên chứa hai số nguyên ~a, b~ (~|a|, |b| \le 10^9~).
• Dòng thứ hai chứa hai số nguyên ~a', b'~ (~|a'|, |b'| \le 10^9~).

Output

• Nếu ~(D)~ và ~(\Delta)~ song song, in ra kết quả theo đúng cú pháp là Parallel.
• Nếu ~(D)~ và ~(\Delta)~ trùng nhau, in ra kết quả theo đúng cú pháp là Coincident.
• Nếu ~(D)~ và ~(\Delta)~ cắt nhau, in ra kết quả theo đúng cú pháp là Intersect X Y, với ~(X, Y)~ là tọa độ giao điểm của hai đường thẳng này. Hãy in ra ~X, Y~ với đúng 6 chữ số sau dấu thập phân.

Ví dụ

Input

2 3
3 4

Output

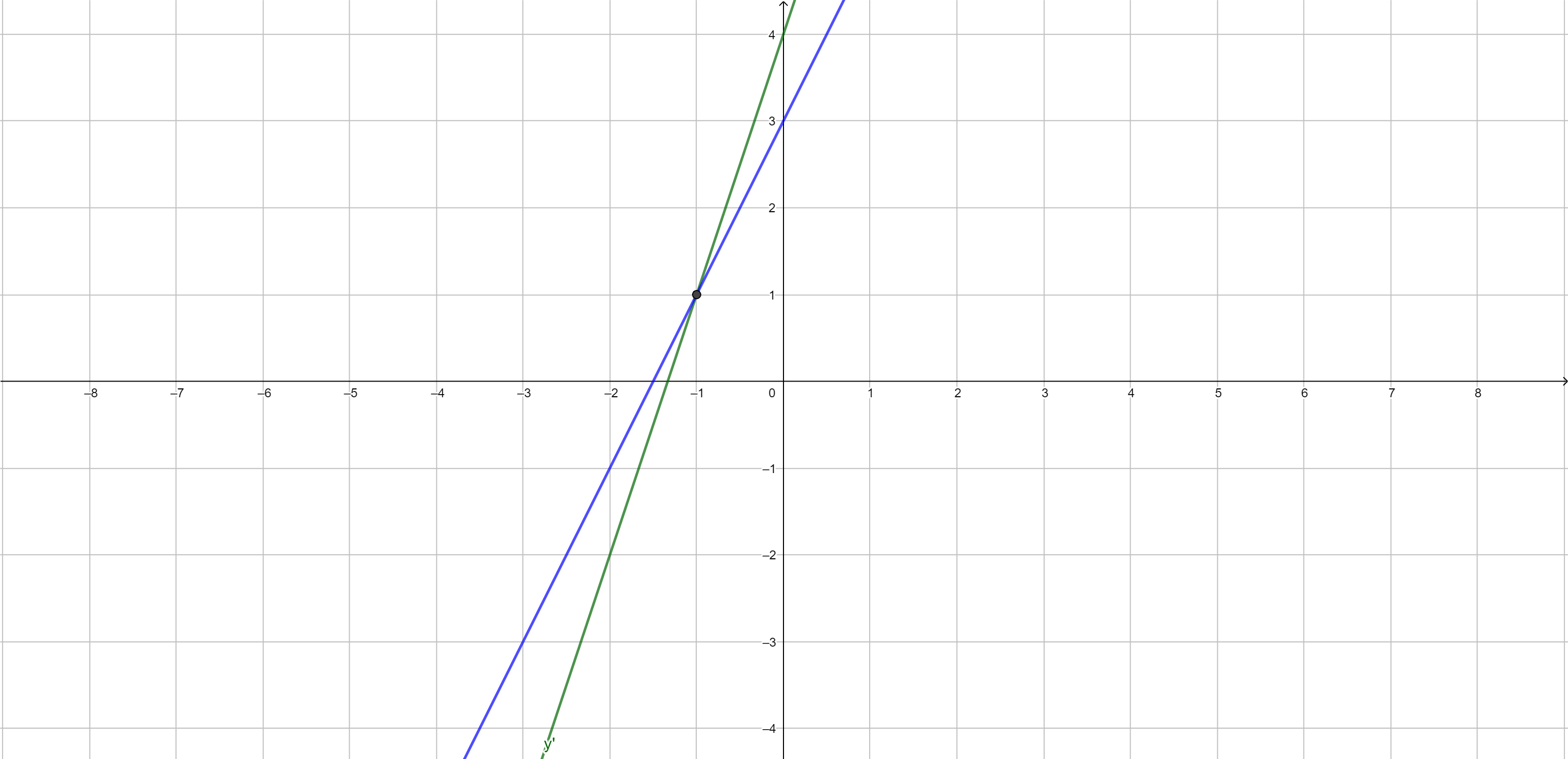
Intersect -1.000000 1.000000

Giải thích

Xem hình bên dưới, với đường màu xanh nước biển là đường thẳng ~(D): y=2x+3~, đường màu xanh lá cây là đường thẳng ~(\Delta): y'=3x+4~.

Cho một xâu ~X~ có độ dài xâu không quá ~10^4~, chỉ gồm các kí tự tiếng Anh in hoa. Viết liên tiếp ~K~ lần xâu ~X~ được xâu ~S~. Hỏi có bao nhiêu xâu HN được tạo ra bằng cách xoá các kí tự từ xâu ~S~.

Dữ liệu vào từ tệp văn bản: DEMHN.INP

• Dòng đầu tiên chứa xâu ~X~;
• Dòng thứ hai chứa một số nguyên dương ~K~ (~K \leq 10^9~).

Kết quả ghi ra tệp văn bản: DEMHN.OUT

• In ra kết quả của bài toán sau khi chia lấy dư cho ~10^9 + 7~.

Subtasks

• Subtask 1 (~50\%~ số điểm): ~K = 1~;
• Subtask 2 (~20\%~ số điểm): ~K \leq 10^3~;
• Subtask 3 (~20\%~ số điểm): ~K \leq 10^6~;
• Subtask 4 (~10\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input

HNNH
2

Sample Output

8

Giải thích

• Xâu ~S~ có dạng HNNHHNNH.
• Các bộ vị trí tạo thành xâu HN thỏa mãn là ~(1, 2), (1, 3), (1, 6), (1, 7), (4, 6), (4, 7), (5, 6), (5, 7)~.

Cho một đồ thị vô hướng ~G~ gồm ~N~ đỉnh đánh số từ ~1~ đến ~N~, được nối với nhau bằng ~M~ cạnh. Mỗi cạnh có độ dài bằng ~1~. Đồ thị này sẽ có một đỉnh trung tâm là ~C~.

Cho biết đỉnh ~C~, hãy tính khoảng cách đường đi ngắn nhất từ đỉnh ~C~ đến các đỉnh trong đồ thị.

Input

• Dòng đầu tiên gồm ~3~ số nguyên dương ~N, M, C~ (~1 \leq N, M \leq 10^5, 1 \leq C \leq N~).
• ~M~ dòng tiếp theo, mỗi dòng gồm ~2~ số ~u, v~ thể hiện một cạnh nối giữa đỉnh ~u~ và đỉnh ~v~.

Output

• In ra ~N~ dòng, mỗi dòng gồm ~2~ số ~x~ ~y~ với ~x~ là số nhãn của đỉnh và ~y~ là khoảng cách ngắn nhất từ đỉnh ~C~ đến ~x~.
• Lưu ý:
  • Khoảng cách từ ~C~ đến chính nó bằng ~0~.
  • Các cặp số cần được in theo thứ tự tăng dần theo khoảng cách. Nếu ~2~ đỉnh có khoảng cách bằng nhau thì nhãn nào nhỏ hơn sẽ đứng trước.
  • Nếu không có đường đi từ ~C~ đến đỉnh ~i~ thì không cần in ra đỉnh ~i~.

Sample Test