Cho một dãy số ~A~ gồm ~N~ số nguyên ~A_1, A_2, \ldots, A_N~. Hãy tìm dãy con tăng dài nhất thuộc dãy ~A~.

Một dãy con tăng độ dài ~k~ thuộc dãy ~A~ có dạng là dãy ~A_{i_1}, A_{i_2}, A_{i_3}, \ldots, A_{i_{k - 1}}, A_{i_k}~ với

• ~1 \leq i_1 < i_2 < \ldots < i_k \leq N~;
• ~A_{i_1} < A_{i_2} < \ldots < A_{i_k}~.

Input

• Dòng thứ nhất gồm một số nguyên dương ~N~ - kích thước dãy ~A~ (~1 \leq N \leq 10^3~)
• Dòng thứ hai gồm ~N~ số nguyên ~A_1, A_2, \ldots, A_N~ (~|A_i| \leq 10^3~).

Output

• Dòng thứ nhất in ra độ dài của dãy con tăng dài nhất của dãy ~A~.
• Dòng thứ hai in ra các vị trí trong dãy ~A~ của các phần tử thuộc dãy con nói trên, các số tăng dần và cách nhau ít nhất ~1~ khoảng trắng. Nếu có nhiều dãy con thoả mãn, in ra các vị trí có thứ tự từ điển nhỏ nhất.

Sample Test 1

Input:

8
2 -1 1 4 1 -5 2 3

Output:

4
2 3 7 8

Sample Test 2

Input:

5
1 2 -10 0 3

Output

3
1 2 5

Một phòng họp do bạn quản lý được ~N~ cuộc họp đặt lịch. Cuộc họp thứ ~i~ có thời gian bắt đầu là ~A_i~ và kết thúc tại thời điểm ~B_i~ (~A_i < B_i~). Hai cuộc họp không thể cùng đồng thời diễn ra, nói cách khác cuộc họp thứ ~j~ chỉ có thể được bố trí sau cuộc họp thứ ~i~ nếu ~B_j \leq A_i~.

Là người quản lý phòng họp, bạn hãy sắp xếp lịch để bố trí nhiều cuộc họp diễn ra nhất có thể.

Input

• Dòng thứ nhất gồm một số nguyên dương ~N~ (~1 \leq N \leq 10^3~).
• Trong ~N~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên dương ~A_i~ và ~B_i~ (~A_i < B_i \leq 10^3~).

Output

• In ra số lượng cuộc họp nhiều nhất có thể bố trí.

Sample Test

Input:

5
1 2
3 7
2 5
4 6
6 8

Output:

3

Note:

• Chọn cuộc họp ~1, 3, 5~.

Một phòng họp do bạn quản lý được ~N~ cuộc họp đặt lịch. Cuộc họp thứ ~i~ có thời gian bắt đầu là ~A_i~, kết thúc tại thời điểm ~B_i~ và trả tiên thuê là ~C_i~ (~A_i < B_i~). Hai cuộc họp không thể cùng đồng thời diễn ra, nói cách khác cuộc họp thứ ~j~ chỉ có thể được bố trí sau cuộc họp thứ ~i~ nếu ~B_j \leq A_i~.

Là người quản lý phòng họp, bạn hãy sắp xếp lịch bố trí các cuộc họp để thu được lợi nhuận lớn nhất có thể.

Input

• Dòng thứ nhất gồm một số nguyên dương ~N~ (~1 \leq N \leq 10^3~).
• Trong ~N~ dòng tiếp theo, dòng thứ ~i~ chứa ba số nguyên dương ~A_i, B_i, C_i~ (~A_i < B_i; B_i, C_i \leq 10^3~).

Output

• In ra lợi nhuận lớn nhất có thể thu được.

Sample Test

Input:

5
1 2 1
3 7 4
5 7 2
3 5 1
7 8 2

Output:

7

Note:

• Chọn cuộc họp ~1, 2, 5~.

Cho một dãy số ~A~ gồm ~N~ số nguyên ~A_1, A_2, \ldots, A_N~. Hãy tìm dãy con đổi dấu dài nhất thuộc dãy ~A~.

Một dãy con đổi dấu độ dài ~k > 1~ thuộc dãy ~A~ có dạng là dãy ~A_{i_1}, A_{i_2}, A_{i_3}, \ldots, A_{i_{k - 1}}, A_{i_k}~ với các điều kiện sau:

• Các phần tử liên tiếp khi so sánh lần lượt "đổi dấu" liên tục: ~A_{i_1} < A_{i_2}, A_{i_2} > A_{i_3}, A_{i_3} < A_{i_4}, \ldots~ hoặc ~A_{i_1} > A_{i_2}, A_{i_2} < A_{i_3}, A_{i_3} > A_{i_4}, \ldots~;
• Các phần tử có chỉ số tăng dần và cách nhau ít nhất ~L~ đơn vị: ~i_2 - i_1 \geq L~, ~i_3 - i_2 \geq L, \ldots, i_k - i_{k - 1} \geq L~;
• Các phần tử liên tiếp có chênh lệch không quá ~U~: ~|A_{i_1} - A_{i_2}| \leq U, |A_{i_2} - A_{i_3}| \leq U, \ldots, |A_{i_{k - 1}} - A_{i_k}| \leq U~.

Dãy gồm một phần tử cũng được coi là một dãy đổi dấu.

Input

• Dòng thứ nhất gồm 3 số nguyên dương ~N, L, U~ (~L < N \leq 10^3~, ~U \leq 10^3~)
• Dòng thứ hai gồm ~N~ số nguyên ~A_1, A_2, \ldots, A_N~ (~|A_i| \leq 10^3~).

Output

• In ra độ dài của dãy con đan dấu dài nhất.

Sample Test 1

Input:

8 2 3
2 -1 1 4 1 -5 2 3

Output:

3

Note

• Chọn dãy con ~-1, 1, 3~ (vị trí ~2, 5, 8~).

Một đêm nọ, một tên trộm nọ quyết định đột nhập vào một siêu thị nọ. Siêu thị có ~N~ đồ vật, vật thứ ~i~ có trọng lượng ~A_i~, giá trị ~B_i~. Tên trộm mang theo một cái túi chứa được trọng lượng tối đa ~W~. Hỏi tổng giá trị tối đa tên trộm có thể lấy được là bao nhiêu?

Input

• Dòng thứ nhất gồm hai số nguyên dương ~N~ và ~W~ (~1 \leq N, W \leq 10^3~).
• Trong ~N~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên dương ~A_i~ và ~B_i~ (~A_i, B_i \leq 10^3~).

Output

• In ra tổng giá trị lớn nhất có thể được lấy đi.

Sample Test

Input:

5 15
12 4
2 2
1 1
1 2
4 10

Output:

15

Cho một dãy số ~A~ gồm ~N~ số nguyên dương ~A_1, A_2, \ldots, A_N~ và một số nguyên dương ~S~. Hãy tìm ~1~ dãy con có tổng ~S~ thuộc dãy ~A~.

Một dãy con tổng ~S~ thuộc dãy ~A~ có dạng là dãy ~A_{i_1}, A_{i_2}, A_{i_3}, \ldots, A_{i_{k - 1}}, A_{i_k}~ với

• ~1 \leq i_1 < i_2 < \ldots < i_k \leq N~;
• ~A_{i_1} + A_{i_2} + \ldots + A_{i_k} = S~.

Input

• Dòng thứ nhất gồm hai số nguyên dương ~N~ và ~S~ (~N, S \leq 10^3~)
• Dòng thứ hai gồm ~N~ số nguyên dương ~A_1, A_2, \ldots, A_N~ (~A_i \leq 10^3~).

Output

• Nếu dãy con tổng ~S~ tổn tại, in ra các chỉ số trong ~A~ của phần tử thuộc dãy con đó. Nếu có nhiều dãy con thoả mãn thì in ra các chỉ số có thứ tự từ điển nhỏ nhất. Ngược lại, nếu không có dãy con thoả mãn thì in ra Does not exist.

Sample Test 1

Input:

5 7
1 3 5 9 3

Output:

1 2 5

Sample Test 2

Input:

4 17
1 3 5 7

Output:

Does not exist

Có ~N~ gói kẹo, gói thứ ~i~ chứa ~A_i~ viên kẹo. Hãy chia các gói thành ~2~ phần sao cho chênh lệch số viên kẹo giữa 2 phần là ít nhất.

Input

• Dòng thứ nhất gồm một số nguyên dương ~N~ (~1 \leq N \leq 100~).
• Dòng tiếp theo chứa ~N~ số ~A_1, A_2, \ldots, A_N~ (~A_i \leq 50~).

Output

• In ra chênh lệch nhỏ nhất số viên kẹo giữa ~2~ nhóm kẹo.

Sample Test 1

Input:

5
2 4 9 3 5

Output:

1

Cho 1 xâu nguồn ~X~ và một xâu đích ~F~. Bạn có thể thực hiện ba thao tác sau trên xâu ~X~:

• Chèn ~1~ kí tự vào sau kí tự thứ ~i~.
  • Ví dụ: ~abcd \rightarrow abecd~.
• Thay thế kí tự ở vị trí thứ ~i~ bằng kí tự C.
  • Ví dụ: ~abcd \rightarrow abce~.
• Xoá kí tự ở vị trí thứ ~i~.
  • Ví dụ: ~abcd \rightarrow abd~.

Tính số lượng thao tác ít nhất để biến đổi xâu ~X~ thành xâu ~F~.

Input

• Dòng thứ nhất chứa xâu ~X~.
• Dòng thứ hai chứa xâu ~F~.
• Hai xâu chỉ gồm các chữ cái thường và độ dài hai xâu không vượt quá ~10^3~.

Output

• In ra số lượng thao tác ít nhất.

Sample Test

Input:

abcd
bde

Output:

3

Cho ~2~ xâu ~A~ và ~B~. Tìm dãy con chung dài nhất của ~2~ xâu này.

Một dãy con của một xâu là xâu thu được sau khi xoá một số kí tự (có thể xoá ~0~ kí tự hoặc xoá toàn bộ kí tự) và giữ nguyên thứ tự của các kí tự còn lại.

Input

• Dòng thứ nhất chứa xâu ~A~.
• Dòng thứ hai chứa xâu ~B~.
• Hai xâu chỉ gồm các chữ cái thường và độ dài hai xâu không vượt quá ~10^3~.

Output

• In ra số lượng thao tác ít nhất.

Sample Test 1

Input:

bbus
uii

Output:

1

Sample Test 2

Input:

uapjhvvjlrilrkuleah
faoipjzllkluegle

Output:

9

Cho một xâu ~S~, hãy tìm số kí tự ít nhất cần thêm vào ~S~ để ~S~ trở thành xâu đối xứng.

Một xâu gọi là xâu đối xứng (palindrome) nếu xâu đó đọc từ trái sang phải hay từ phải sang trái đều như nhau.

Input

• Gồm một xâu S duy nhất chứa các kí tự thường (~|S| \leq 1000~).

Output

• In ra số lượng kí tự ít nhất cần thêm.

Sample Test 1

Input:

bbubbs

Output:

1

Một đêm nọ, một tên trộm nọ quyết định đột nhập vào một siêu thị nọ. Siêu thị có ~N~ mặt hàng, mặt hàng thứ ~i~ có trọng lượng ~A_i~, giá trị ~B_i~ và có thể coi một mặt hàng có vô hạn số lượng hàng. Tên trộm mang theo một cái túi chứa được trọng lượng tối đa ~W~. Hỏi tổng giá trị tối đa tên trộm có thể lấy được là bao nhiêu?

Input

• Dòng thứ nhất gồm hai số nguyên dương ~N~ và ~W~ (~1 \leq N, W \leq 10^3~).
• Trong ~N~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên dương ~A_i~ và ~B_i~ (~A_i, B_i \leq 10^3~).

Output

• In ra tổng giá trị lớn nhất có thể được lấy đi.

Sample Test

Input:

2 100
1 1
50 49

Output:

100

Ở đất nước Omega người ta chỉ tiêu tiền xu. Có ~N~ loại tiền xu, loại thứ ~i~ có mệnh giá là ~A_i~ đồng. Một người khách du lịch đến Omega du lịch với số tiền ~M~ đồng. Ông ta muốn đổi số tiền đó ra tiền xu Omega để tiện tiêu dùng.

Bạn hãy giúp ông ta tìm ~1~ cách đổi tiền để số đồng tiền đổi được là ít nhất (cho túi tiền đỡ nặng khi đi đây đi đó).

Input

• Dòng thứ nhất gồm hai số nguyên dương ~N~ và ~M~ (~N \leq 100, M \leq 10^3~).
• Dòng thứ hai gồm ~N~ số nguyên dương ~A_1, A_2, \ldots, A_N~ khác nhau (~A_i \leq 10^3, A_1 = 1~).

Output

• In ra số lượng đồng tiền ít nhất để đổi ~M~ đồng thành xu Omega.

Sample Test

Input:

3 8
1 4 5

Output:

2

Một ma trận ~A~ kích thước ~m \times n~ có thể biểu diễn dưới dạng:

$$ \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \ldots\\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix} $$

Phép nhân giữa ma trận ~A~ kích thước ~m \times n~ và ma trận ~B~ kích thước ~n \times p~ là một ma trận ~C~ có kích thước ~m \times p~, với

$$ \begin{equation} C_{ij} = \sum^{n}_{k=1} A_{ik} \times B_{kj} \space (1 \leq i \leq m, 1 \leq j \leq p) \end{equation} $$

Như vậy, nhân ~A~ với ~B~ ta cần thực hiện tổng cộng ~m \times n \times p~ phép toán. Để dễ hiểu hơn ta có thể minh hoạ phép nhân ma trận như sau:

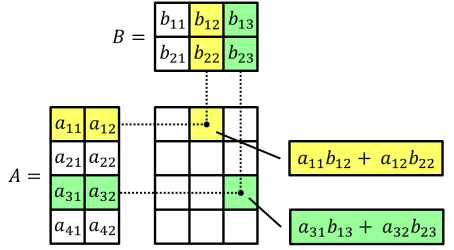
Ma trận không có tính giao hoán, tuy nhiên vẫn có tính kết hợp, tức là ~(A \times B) \times C~ = ~A \times (B \times C)~. Số lượng phép tính cần thực hiện cho ~2~ trình tự tính là khác nhau.

Cho ~N~ ma trận ~A_1, A_2, \ldots, A_N~, ma trận ~i~ có kích thước ~d_{i - 1} \times d_i~. Hãy xác định trình tự nhân ma trận ~A_1 \times A_2 \times \ldots \times A_N~ sao cho số phép nhân cần thực hiện là ít nhất.

Input

• Dòng thứ nhất gồm số nguyên dương ~N~ (~N \leq 100~).
• Dòng thứ hai gồm ~N + 1~ số nguyên dương ~d_0, d_1, d_2 \ldots, d_N~ (~d_i \leq 100~).

Output

• In ra số phép tính ít nhất cần để thực hiện biểu thức nhân ma trận.

Sample Test

Input:

4
40 20 30 10 30

Output:

26000

Note:

• Có 4 ma trận ~A_{40 \times 20}, B_{20 \times 30}, C_{30 \times 10}, D_{10 \times 30}~.
• Trinh tự nhân tối ưu: ~(A \times (B \times C)) \times D~.
• Số lượng phép tính: ~20 \times 30 \times 10 + 40 \times 20 \times 10 + 40 \times 10 \times 30 = 26000~.

Có ~n~ lọ hoa sắp thẳng hàng và ~k~ bó hoa được đánh số thứ tự từ nhỏ đến lớn. Cần cắm ~k~ bó hoa trên vào ~n~ lọ sao cho hoa có số thứ tự nhỏ phải đứng trước hoa có số thứ tự lớn. Giá trị thẩm mỹ tương ứng khi cắm bó hoa thứ ~i~ vào lọ thứ ~j~ là ~v_{i, j}~.

Hãy tìm ~1~ cách cắm sao cho tổng giá trị thẩm mỹ là lớn nhất. Chú ý rằng mỗi bó hoa chỉ được cắm vào ~1~ lọ và mỗi lọ cũng chỉ cắm được ~1~ bó hoa.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~k~ (~k \leq n~).
• ~k~ dòng tiếp theo, mỗi dòng gồm ~n~ số nguyên dương ~v_{k, 1}, v_{k, 2}, \ldots, v_{k, n}~ mô tả giá trị thẩm mỹ khi cắm bó hoa thứ ~k~ vào lần lượt lọ hoa thứ ~1, 2, \ldots, n~.
• Giá trị các số trong phần Input không vượt quá ~10^3~.

Output

• In ra tổng giá trị thẩm mỹ lớn nhất.

Sample Test

Input:

3 2
5 7 5
8 9 6

Output:

14

Có ~N~ phòng học chuyên đề và ~K~ nhóm học được đánh số thứ tự từ nhỏ đến lớn. Phòng thứ ~i~ có ~a_i~ ghế và nhóm thứ ~j~ có ~b_j~ học sinh. Thầy giáo cần xếp các nhóm trên vào các phòng học sao cho nhóm có số hiệu nhỏ được xếp vào phòng có số hiệu nhỏ, nhóm có số hiệu lớn phải được xếp vào phòng có số hiệu lớn. Với mỗi phòng được xếp, số học sinh phải bằng số ghế thừa, tức các ghế thừa phải được chuyển ra hết, nếu thiếu ghế thì lấy vào cho đủ ghế.

Hãy chọn ~1~ phương án bố trí sao cho tổng số lần chuyển ghế ra và vào là ít nhất.

Input

• Dòng thứ nhất chứa ~2~ số nguyên dương ~N~ và ~K~ (~K < N \leq 10^3~).
• Dòng thứ hai chứa ~N~ số nguyên dương ~a_1, a_2, \ldots, a_N~ (~a_i \leq 10^3~).
• Dòng thứ ba chứa ~K~ số nguyên dương ~b_1, b_2, \ldots, b_K~ (~b_i \leq 10^3~).

Output

• In ra tổng số lần chuyển ghế ít nhất.

Sample Test

Input:

10 2
4 7 9 6 1 10 1 4 3 6
3 1

Output:

1

Cho bảng ~A~ gồm ~M \times N~ ô được đánh số theo thứ tự từ trên xuống dưới, trái sang phải. Từ ô ~(i,j)~ có thể di chuyển sang ~3~ ô ~(i + 1, j), (i + 1,j – 1)~ và ~(i + 1,j + 1)~ (nếu ô đấy tồn tại). Hãy xác định một lộ trình đi, xuất phát từ ~1~ ô bất kì hàng ~1~ đến ~1~ ô bất kì hàng ~M~ sao cho tổng các ô đi qua là nhỏ nhất.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~M~ và ~N~.
• ~M~ dòng tiếp theo, mỗi dòng chứa ~N~ số nguyên dương mô tả bảng số.
• Giá trị các số trong phần Input đều không vuợt quá ~10^3~.

Output

• In ra tổng giá trị nhỏ nhất đạt được.

Sample Test

Input:

3 3
2 3 5
2 3 1
3 4 2

Output:

6

Note:

• Lộ trình đi: ~(1, 2) \rightarrow (2, 3) \rightarrow (3, 3)~.

Cho một bảng vuông ~n \times n~ ô, một số ô có thể có bẫy. Các ô được đánh thứ tự trên trên xuống dưới, từ trái sang phải.

Nhiệm vụ của bạn là tính số lượng cách đi từ ô trái trên (toạ độ ~(1, 1)~) đến ô phải dưới (toạ độ ~(n, n)~) mà không đi qua bẫy. Bạn chỉ có thể di chuyển sang phải hoặc xuống dưới.

Input

• Dòng đầu tiên chứa số nguyên dương ~n~ - kích thước bảng (~n \leq 1000~).
• ~n~ dòng tiếp theo, mỗi dòng chứa ~n~ kí tự mô tả bảng vuông:
  • . mô tả một ô trống (có thể đi qua);
  • * mô tả một ô có bẫy (không thể đi qua).

Output

• In ra số lượng đường đi, lấy phần dư khi chia cho ~10^9 + 7~.

Sample Test

Có ~n~ người xếp hàng mua vé một trận bóng theo thứ tự ~1~ đến ~n~. Mỗi người cần mua một vé, nhưng người bán vé lại có thể bán cho mỗi người tối đa hai vé. Do đó, một số người có thể rời hàng và nhờ người đứng trước mình mua hộ vé. Biết ~t_i~ là thời gian cần thiết để người thứ ~i~ mua vé cho mình. Nếu người thứ ~i+1~ rời hàng và nhờ người ~i~ mua hộ vé thì mất ~r_i~ thời gian để mua cho cả hai.

Hãy xác định thời gian mua vé nhỏ nhất.

Input

• Dòng đầu chứa số nguyên dương ~n~ ~(n \le 6*10^4)~
• Dòng thứ hai chứa ~n~ số nguyên dương miêu tả dãy ~t[1], t[2], ..., t[n]~.~(t[i] \le 30000)~
• Dòng thứ ba chứa ~n-1~ số nguyên dương miêu tả dãy ~r_[1], r_[2], ..., r_[n-1]~. ~(r[i] \le 30000)~

Output

• In ra thời gian ít nhất để mua vé cho ~n~ người.

Sample Test

Input

5
2 5 7 8 4
4 9 10 10

Output

18

Hôm nay Rùa cần di chuyển ~k~ km để tới điểm hẹn với Thỏ. Nhưng đợt này xe trong thành phố chuyển thành xe buýt điện, nên mỗi xe chỉ có thể đi được không quá ~n~ km. Xe buýt mà đi được ~i~ km thì cần mua vé tương ứng là ~a_i~ đồng. Hãy tính giúp bạn Rùa để bạn lên xuống xe thế nào mà số tiền phải trả để mua vé là nhỏ nhất.

INPUT

Dòng đầu tiên chứa hai số nguyên dương ~n, k~ (~n \le 100, k \le 2000~)

Dòng tiếp theo chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ (~a_i \le 10000~)

OUTPUT

Dòng duy nhất ghi tổng số tiền phải trả và số lần lên xe, cách nhau bởi một dấu cách.

Nếu có nhiều cách chọn thoả mãn tổng số tiền phải trả là nhỏ nhất, in ra cách có số lần lên xe ít nhất.

SAMPLE INPUT

4 5
3 1 2 4

SAMPLE OUTPUT

3 2

Giải thích:

• Lần ~1~: đi ~3~ km hết ~2~ đồng.
• Lần ~2~: đi ~2~ km hết ~1~ đồng.

Tỉnh A đang triển khai rất nhiều dự án xây dựng cơ sở hạ tầng cho Thành Phố. Tập đoàn xây dựng của hoangduong nhận được lời mời thầu ~n~ dự án (đánh số từ ~1~ đến ~n~). Sau khi tính toán thì tập đoàn này thấy để xây dựng dự án thứ ~i~ sẽ cần số vốn là ~c_i~ và sau khi hoàn thành sẽ thu hồi được vốn và thu được lợi nhuận là ~p_i~. Tập đoàn này có thể chọn thầu một số dự án bất kỳ trong danh sách trên và với những dự án được chọn, tập đoàn này phải bỏ toàn bộ vốn ra xây dựng và khi hoàn thành mới được thanh toán toàn bộ cả vốn lẫn lời.

Hiện tại, tập đoàn của hoangduong đang có số vốn là ~s~. Bạn hãy giúp cho tập đoàn này lựa chọn các dự án để nhận thầu sao cho có đủ vốn để xây dựng các dự án này và thu về lợi nhuận lớn nhất có thể nhé.

INPUT

Dòng đầu chứa hai số nguyên dương ~n~ và ~s~ (~1 \le n \le 30~; ~1 \le s \le 300000~)

Dòng thứ hai chứa ~n~ số nguyên dương ~c_1, c_2, ..., c_n~ (~1 \le c_i \le 10000~)

Dòng thứ ba chứa ~n~ số nguyên dương ~p_1, p_2, ..., p_n~ (~1 \le p_i \le 10000~)

OUTPUT

Một số nguyên duy nhất là lợi nhuận lớn nhất có thể được.

SAMPLE INPUT

3 10 
4 5 7 
3 4 8

SAMPLE OUTPUT

8

Phát minh mới nhất của của Nitori là một chiếc máy bay ném bom điều khiển từ xa. Ba nàng tiên ánh sáng đã đặt một chiếc cho kế hoạch khủng bố đền Hakurei.

Dĩ nhiên để máy bay có thể hoạt động thì cần có pin. Mỗi cục pin có 3 thông tin: ~e_i, w_i, c_i~ lần lượt và mức năng lượng, khối lượng và giá thành. Thời gian bay của máy bay được xác định bằng công thức: ~E\over{W}~ trong đó ~E~ là tổng mức năng lượng và ~W~ là tổng khối lượng của tất cả pin và khối lượng của máy bay.

Để đảm bảo kế hoạch thành công, máy bay cần hoạt động lâu nhất có thể. Ba nàng tiên có ngân sách ~b~ và khối lượng của máy bay là ~w~, hãy giúp họ chọn pin sao cho thời gian bay là lâu nhất!

Input:

• Dòng đầu chứa số ~n,b,w (1≤n×b≤10^5,1≤w≤1000)~.

• ~n~ dòng tiếp theo mỗi dòng chứa ba số ~e_i,w_i,c_i (0≤e_i,w_i≤1000,0≤c_i≤b)~ là mức năng lượng, khối lượng và giá thành của cục pin thứ ~i~.

Output:

• In ra tổng thời gian bay của máy bay, sai số không quá ~10^{-3}~.

Sample Test:

Input:

10 1000 20
40 40 40
1 1 1
70 30 60
100 20 700
80 50 200
30 1 200
100 100 1
20 1 500
30 20 100
70 50 100

Output:

3.1707

Giới hạn

• 25% số điểm ~n≤20~.
• 25% số điểm ~w_i=0~.
• 25% số điểm ~c_1=c_2=...=c_n~.
• 25% số điểm không có ràng buộc gì thêm.

Alice Margatroid cần dọn tuyết trên mái nhà. Cô sẽ dùng chọn ra ~m~ con búp bê của mình để thực hiện nhiệm vụ. Alice có ~n~ thùng đựng búp bê, thùng thứ ~i~ có ~a_i~ con, và cô muốn mỗi thùng chỉ được chọn ra tối đa 1 con búp bê. Hỏi có bao nhiêu cách để chọn ra ~m~ con búp bê.

Input

• Dòng đầu tiên gồm 2 số tự nhiên ~n, m~ ~(1 \le m \le n \le 1000)~
• Dòng tiếp theo gồm ~n~ số tự nhiên là số lượng búp bê của từng thùng. (~1 \le a[i] \le 10^9~)

Output

• Gồm 1 số tự nhiên duy nhất là số cách chọn búp bê modulo ~10^9 + 7~

Sample Test

Input:

3 2
1 2 1

Output:

5

Giải thích:

• Có 5 cách chọn là: ~\{1, 2.1\}, \{1, 2.2\}, \{1, 3\}, \{2.1, 3\}, \{2.2, 3\}~ với ~x.y~ là con búp bê thứ ~y~ của thùng thứ ~x~

Cho dãy gồm ~n~ số nguyên ~a_1, a_2, \dots, a_n~ chỉ gồm các số ~1~, ~2~ và ~3~. Đếm số cách xoá một vài phần tử của dãy (có thể không xoá) để nhận được một dãy thoả mãn hai yêu cầu sau:

1. Dãy còn ít nhất ~3~ phần tử
2. Phần tử đầu tiên của dãy có giá trị ~1~, tiếp theo là một số phần tử có giá trị ~2~ (ít nhất một số ~2~), kết thúc bằng đúng một phần tử có giá trị ~3~.

Ví dụ: các dãy ~\{1, 2, 2, 3\}~ và dãy ~\{1, 2, 3\}~ thoả mãn yêu cầu, các dãy ~\{1, 2, 3, 3\}~ và dãy ~\{1, 1, 2, 3\}~ không thoả mãn yêu cầu.

Vì số cách xoá có thể rất lớn, hãy in ra số cách xoá chia lấy dư cho ~10^9+7~.

Input

Dòng đầu chứa số nguyên ~n~ (~1 \le n \le 10^6~) là số lượng phần tử của dãy.

Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \dots, a_n~ (~1 \le a_i \le 3~) mô tả các phần tử của dãy.

Output

Gồm một dòng duy nhất chứa một số nguyên là số cách xoá thoả mãn yêu cầu đề bài, chia lấy dư cho ~10^9+7~.

Example

Input

8
1 2 1 2 3 1 2 3

Output

15

Đã là sản phẩm thì phải có mã vạch ở trên nên Nitori quyết định in mã vạch cho sản phẩm dưa chuột của mình. Cô muốn mã vạch có kích thước ~n \times m~, kí tự # thể hiện màu đen còn . thể hiện màu trắng. Các cột của mã vạch phải cùng màu, số lượng cột cùng màu nhau ở cạnh nhau ít nhất là ~x~ và nhiều nhất là ~y~.

Do máy in bị trục trặc nên mã vạch đã bị in sai hết cả. Nitori muốn tiết kiệm chi phí nên hãy đếm số lượng ít nhất kí tự phải sửa để được mã vạch thỏa mãn yêu cầu nhé!

Input

• Dòng đầu tiên gồm các số nguyên dương ~1 \le n, m, x, y \le 1000~.
• ~n~ dòng tiếp theo gồm ~m~ kí tự thuộc # hoặc ..

Output

• Số lượng kí tự ít nhất phải sửa.

Sample Test

Input:

6 5 1 2
##.#.
.###.
###..
#...#
.##.#
###..

Output:

11

Polygon là một game cho một người chơi, bắt đầu từ một đa giác có ~N~ đỉnh. Mỗi đỉnh chứa một số nguyên và mỗi cạnh chứa một dấu (+ hoặc *). Các cạnh được đánh số từ ~1~ đến ~N~.

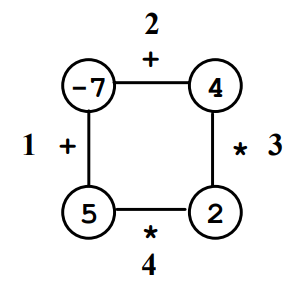
Ở bước đầu tiên, một trong các cạnh bị xoá đi.

Các bước tiếp theo bao gồm các thao tác sau:

• Chọn một cạnh ~E~ và hai đỉnh ~V_1~, ~V_2~ mà được nối với nhau bởi cạnh E;
• Thay thế chúng bằng một đỉnh mới, đỉnh này chứa kết quả của phép tính hai số trên ~V_1~ và ~V_2~ với dấu trên cạnh ~E~.

Trò chơi kết thúc khi không còn cạnh nào nữa, và điểm của trò chơi chính là giá trị trên đỉnh còn lại cuối cùng.

Mô phỏng trò chơi:

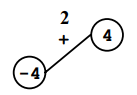
Sử dụng ví dụ là đa giác như trên. Người chơi bắt đầu bằng cách bỏ đi cạnh ~3~:

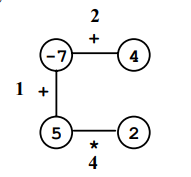
Tiếp theo, người chơi chọn cạnh ~1~, và thay thế cạnh đó với ~2~ đỉnh ~-7~ và ~5~ bằng kết quả phép tính ~-7 + 5~.

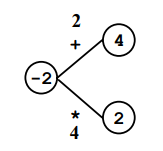
Rồi tiếp theo chọn cạnh ~4~ và cuối cùng là cạnh ~2~:

~\rightarrow~

Điểm cuối cùng của trò chơi là ~0~.

Nhiệm vụ của bạn là: Cho một đa giác, hãy tính số điểm cao nhất có thể đạt được, và đưa ra danh sách các cạnh mà, khi bỏ ở bước đầu tiên, có thể dẫn đến số điểm đó.

Input

• Dòng đầu tiên chứa số nguyên dương ~N~.
• Dòng thứ hai chứa các số nguyên và kí tự cách nhau ~1~ khoảng trắng: Các số nguyên là số trên các đỉnh ~1, 2, \ldots, N~, đan xen giữa các dấu trên các cạnh:
  • Dấu đầu tiên là dấu trên cạnh nối đỉnh ~1~ và đỉnh ~2~, dấu tiếp theo là dấu trên cạnh ~2~ nối đỉnh ~2~ và đỉnh ~3~, ~\ldots~, dấu cuối cùng là dấu trên cạnh nối đỉnh ~N~ và đỉnh ~1~.
  • Dấu trên cạnh được biểu diễn bằng kí tự t (dấu cộng) hoặc kí tự x (dấu nhân).

Output

• Dòng đầu tiên in ra số điểm lớn nhất có thể đạt được cho đa giác ở phần Input.
• Dòng thú hai in ra chỉ số các cạnh mà, nếu bỏ ở bước đầu tiên, có thể dẫn đến số điểm đó. Các chỉ số cần được viết theo thứ tự tăng dần, cách nhau một khoảng trắng.

Giới hạn

• ~3 \leq N \leq 50~.
• Trong mọi cách chơi bất kỳ, các số trên các đỉnh luôn đàm bảo nằm trong khoảng ~[-32768, 32767]~.

Sample Test

Input:

4
t -7 t 4 x 2 x 5

Output:

33
1 2

Note:

• Ví dụ trên biểu diễn đa giác mẫu ở đề bài.