Tie2 T9
Dãy Sắc Màu
Nộp bàiPoint: 100
Sau khi chơi với ngọc chán chê, Tí sắp ~n~ viên ngọc ra một đường thẳng và bắt đầu nhìn ngắm chúng. Tí nhận thấy rằng có không quá ~k~ màu ngọc khác nhau trên bàn và viên ngọc thứ ~i~ từ trái sang thì có màu ~a_i~. Tí muốn chia dãy ngọc thành các đoạn liên tiếp sao cho mỗi đoạn đều có đủ ~k~ màu. Hỏi Tí có bao nhiêu cách chia thỏa mãn như vậy?
Yêu cầu: In số cách chia thỏa mãn sau khi ~\mod 10^9+7~
Input
- Dòng đầu tiên chứa hai số nguyên dương ~n,k~.
- Dòng thứ hai chứa ~n~ số nguyên ~a_1,a_2,...,a_n~.
Output
- Ghi ra một số nguyên là kết quả bài toán.
Constraints
- ~1\leq k\leq n\leq 10^6~
- ~1\leq a_i\leq k~
Scoring
- Subtask ~1~ (~20\%~ số điểm): ~k = 1~.
- Subtask ~2~ (~20\%~ số điểm): ~n\leq 5000~.
- Subtask ~3~ (~20\%~ số điểm): ~n\leq 10^5, k\leq 100~.
- Subtask ~4~ (~40\%~ số điểm): Không có ràng buộc gì thêm.
Example
Sample Input ~1~
5 2
1 2 2 1 2
Sample Ouput ~1~
3
Explanation
Có ~3~ cách chia như sau: ~(1\ 2) | (2\ 1\ 2), (1\ 2\ 2) | (1\ 2)~, hoặc ~(1\ 2\ 2\ 1\ 2)~.
Palindrome trên bảng
Nộp bàiPoint: 100
Cho lưới ô vuông kích thước ~n~ x ~n~, các hàng đánh số ~1…n~ từ trên xuống dưới, các cột đánh số ~1…n~ từ trái sang phải. Mỗi ô trong lưới chứa một kí tự chữ cái latin in hoa. Xét các đường đi từ ô ~(1;1)~ đến ô ~(n;n)~ chỉ đi từ một ô sang ô kề cạnh bên phải hoặc bên dưới. Mỗi đường đi được đại diện bởi một xâu kí tự là dãy các kí tự trong các ô trên đường đi dọc theo hành trình. Đếm số đường đi có xâu đại diện là xâu đối xứng.
Input
- Dòng 1: số nguyên ~n~ ~(1 \leq n \leq 500)~.
- Dòng 2…~n+1~: dòng ~i+1~ chứa một xâu độ dài ~n~ mô tả hàng ~i~ của lưới.
Output
- Dòng 1: số nguyên là số lượng đường đi có xâu đại diện là xâu đối xứng, lấy phần dư khi chia cho ~(10^9+7)~.
Subtask
- Có ~30\%~ số test có ~n \le 100~
- ~70\%~ còn lại không giới hạn gì thêm
Sample Input 1
4
ABCD
BXZX
CDXB
WCBA
Sample Output 1
12
Explanation:
- Xâu ABCDCBA là đại diện của 1 đường
- Xâu ABCWCBA là đại diện của 1 đường
- Xâu ABXZXBA là đại diện của 6 đường
- Xâu ABXDXBA là đại diện của 4 đường
Đường Đi Tổng Xor
Nộp bàiPoint: 100
Cho trước một cây chỉ gồm một đỉnh ~1~ (và cũng chính là gốc của cây). Nhiệm vụ của bạn là viết chương trình hỗ trợ thực hiện ~Q~ truy vấn ở hai dạng sau:
Add x y- Thêm một đỉnh vào cây và cho nó làm một đỉnh con của đỉnh ~x~. Đỉnh mới này và đỉnh ~x~ được kết nối bởi một cạnh có trọng số là ~y~. Số hiệu của đỉnh mới bằng số lượng đỉnh của cây trước khi thêm cộng cho ~1~.Query a b- Tìm đường đi dài nhất bắt đầu từ đỉnh ~a~ và kết thúc tại một đỉnh thuộc cây con gốc ~b~ (bao gồm chính đỉnh ~b~). Độ dài của một đường đi được định nghĩa là tổng xor các trọng số của các cạnh nằm trên đường đi đó.
Input
Dòng đầu tiên chứa số nguyên dương ~Q~ ~(1\leq Q\leq 200,000)~ được nhắc đến ở đề bài.
Dòng thứ ~i~ trong ~Q~ dòng tiếp theo chứa thông tin về truy vấn thứ ~i~ ở định dạng đã được mô tả ở đề bài. Các giá trị ~x~, ~a~ và ~b~ thể hiện những đỉnh đang tồn tại ở trong cây tại thời điểm truy vấn và giá trị ~y~ không vượt quá ~2^{30}~.
Output
- Với mỗi truy vấn dạng
Query, in ra một số nguyên trên một dòng riêng biệt thể hiện câu trả lời cho truy vấn tương ứng.
Scoring
- ~25\%~ số test có ~Q\leq 200~.
- ~25\%~ số test khác có ~Q\leq 2000~.
- ~25\%~ số test khác thỏa ~b=1~ với mọi truy vấn
Query. - ~25\%~ số test còn lại không có ràng buộc gì thêm.
Sample Input 1
4
Add 1 5
Query 1 1
Add 1 7
Query 1 1
Sample Output 1
5
7
Sample Input 1
10
Add 1 4
Add 1 9
Add 1 10
Add 2 2
Add 3 3
Add 4 4
Query 4 2
Query 1 3
Add 6 7
Query 1 3
Sample Output 1
14
10
13
New Roads
Nộp bàiPoint: 100
Đất nước ~ABC~ gồm ~n~ thành phố. Chính quyền đang có kế hoạch xây dựng các con đường mới.
Bản kế hoạch gồm các con đường có sẽ xây dựng theo thứ tự và các yêu cầu tính toán giúp chính quyền quản lý đất nước tốt hơn. Thông tin được liệt kê gồm 1 trong 2 loại:
- ~1~ ~u~ ~v~ ~w~: Nếu ~u~ đã có thể đi tới ~v~ bằng những con đường mới, ta loại bỏ đề xuất này. Nếu không, xây dựng con đường mới kết nối từ ~u~ tới ~v~ với độ dài ~w~.
- ~2~ ~u~: Chính quyền muốn biết sau khi những con đường trên được xây, từ thành phố ~u~ có thể đi tới thành phố xa nhất cách đó bao nhiêu xa.
Yêu cầu: Hãy giúp chính quyền tính toán các thông tin trong bản kế hoạch đặt ra.
Input
- Dòng đầu chứa ba số nguyên ~n,m~.
- ~m~ dòng tiếp theo, mỗi dòng chứa ~1~ trong ~2~ loại thông tin trong bản kế hoạch của nhà vua. Dữ liệu đảm bảo sau khi thực hiện hết bản kế hoạch, tất cả các thành phố được kết nối với nhau bằng hệ thống đường mới.
Output
- Đưa ra khoảng cách xa nhất có thể đi được tương ứng với các thông tin loại ~2~. Mỗi kết quả được đưa theo thứ tự, mỗi số trên một dòng.
Subtask
Trong tất cả các test, ~1 \le w \le 10^9~
- Subtask ~1~: ~n,m \le 2 \times 10^3~ ~(30\%)~
- Subtask ~2~: ~n \le 10^5, m \le 3 \times 10^5~ và tất cả các truy vấn loại ~1~ xuất hiện trước các truy vấn loại ~2~. ~(30\%)~
- Subtask ~3~: ~n \le 10^5, n \le 3 \times 10^5~ ~(40\%)~.
Sample Input 1
4 8
1 1 2 4
1 1 3 5
1 2 3 12
1 2 4 3
2 1
2 2
2 3
2 4
Sample Output 1
7
9
12
12
EK Diameter 1
Nộp bàiPoint: 100
Cho một cây gồm ~n~ đỉnh và số nguyên dương ~k~.
Bạn cần xóa một vài cạnh ở trên cây. Sau đó, cây sẽ trở thành một "rừng" với nhiều cây con, tập cạnh bạn xóa được gọi là tốt nếu như tất cả các cây con đều có đường kính không lớn hơn ~k~.
Hãy đếm số tập cạnh thỏa mãn.
Input
- Dòng đầu gồm hai số nguyên dương ~n,k~.
- ~n-1~ dòng tiếp theo, mỗi dòng gồm hai số nguyên ~u~, ~v~ miêu tả cạnh của cây.
Output
- In ra số tập cạnh thỏa mãn theo module ~998244353~.
Constraints
- ~1 \le n,k \le 5 \times 10^3~.
Subtask
- ~30\%~ số điểm có ~n \le 20~.
- ~30\%~ số điểm có ~n \le 100~.
- ~40\%~ số điểm có ~n \le 5000~
Sample Input 1
6 2
1 3
2 4
3 2
1 5
4 6
Sample Output 1
24
XOR 🐦
Nộp bàiPoint: 100
Cho mảng ~a~ gồm ~n~ số nguyên không âm. Đặt ~f(l, r) = a_l \text{ OR } a_{l+1} \text{ OR } ... \text{ OR } a_r~. Yêu cầu: Tính tổng ~\text{ XOR }~ mọi ~f(l, r)~ với (~1 \le l \le r \le n~).
Input: Nhập từ file "BIGBIRD.INP"
- Dòng đầu tiên chứa một số nguyên dương ~n~.
- Dòng thứ hai chứa n số nguyên không âm ~a_1, a_2,..., a_n~.
Output: Xuất ra file "BIGBIRD.OUT"
- Một số nguyên là giá trị cần tính.
Ví dụ
Input:
3
1 4 3
Output
3
Giải thích ví dụ:
~f(1, 1) \text{ XOR } f(1, 2) \text{ XOR } f(1, 3) \text{ XOR } f(2, 2) \text{ XOR } f(2, 3) \text{ XOR } f(3, 3)~ = ~1 \text{ XOR } 5 \text{ XOR } 7 \text{ XOR } 4 \text{ XOR } 7 \text{ XOR } 3~ = ~3~
Giới hạn
~0 \le a_i \le 1e9~
- Subtask 1 (25%): ~n \le 100~
- Subtask 2 (25%): ~n \le 1000~
- Subtask 3 (25%): ~a_i \le 1~
- Subtask 4 (25%): ~n \le 1e5~
Tunnel
Nộp bàiPoint: 100
Software and cathedrals are much the same – first we build them, then we pray 😈
Dưới lòng đất của HNA là hệ thống đường ngầm dày đặc gồm ~n~ địa điểm đánh số từ ~1~ đến ~n~. Có ~m~ đoạn đường ngầm, đoạn đường ngầm thứ ~i~ kết nối địa điểm ~u_i~ và ~v_i~ có chi phí là ~c_i~, nghĩa là muốn kích hoạt sử dụng đoạn đường hầm này phải trả chi phí là ~c_i~.
LetterC67 và ~aúR là đôi bạn thân đang hoạt động dưới lòng đất này.
Buổi sáng, LetterC67 cần đi từ ~A~ đến ~B~, và tất nhiên cậu chọn tuyến đường sao cho cần trả ít chi phí nhất.
Buổi chiều, ~aúR cần đi từ ~C~ đến ~D~, nhưng may thay, những đoạn đường hầm mà buổi sáng LetterC67 đã trả chi phí để kích hoạt rồi thì ~aúR có thể sử dụng mà không cần trả chi phí nữa.
Hãy hãy tính xem ~aúR cần trả chi phí ít nhất là bao nhiêu?
Input: tunnel.inp
- Dòng đầu tiên gồm hai số nguyên ~n, m~.
- Dòng thứ hai là bốn số nguyên ~A, B, C, D~.
- ~m~ dòng tiếp theo, mỗi dòng gồm ba số nguyên ~u_i, v_i, c_i~.
- Dữ liệu đảm bảo từ một địa điểm có thể đi đến mọi địa điểm khác, không có hai đoạn đường hầm nối cùng một cặp địa điểm.
Output: tunnel.out
- In ra một số nguyên là kết quả của bài toán.
Note
- Trong mọi test: ~A \neq B, C \neq D~, ~1 \le u_i < v_i \le n~, ~1 \le c_i \le 10^9~.
- Subtask 1 (~15\%~ số điểm): ~A=C~;
- Subtask 2 (~15\%~ số điểm): Có duy nhất một tuyến đường từ ~A~ đến ~B~ có giá trị nhỏ nhất;
- Subtask 3 (~30\%~ số điểm): ~n \le 300~;
- Subtask 4 (~40\%~ số điểm): ~2 \le n \le 10^5, 1 \le m \le 2 \times 10^5~
Ví dụ
Input:
6 6
1 6 1 4
1 2 5
2 3 1
3 5 1
2 4 3
4 5 2
5 6 1
Output:
2
Giải thích:
- Chỉ có duy nhất một đường đi ngắn nhất từ ~1~ đến ~6~ là ~1-2-3-5-6~, nên
LetterC67sẽ sử dụng tuyến đường này. ~aúRsẽ chỉ phải trả chi phí thêm đoạn đường hầm ~4-5~ với giá trị ~2~ đến di chuyển từ ~1~ đến ~4~.
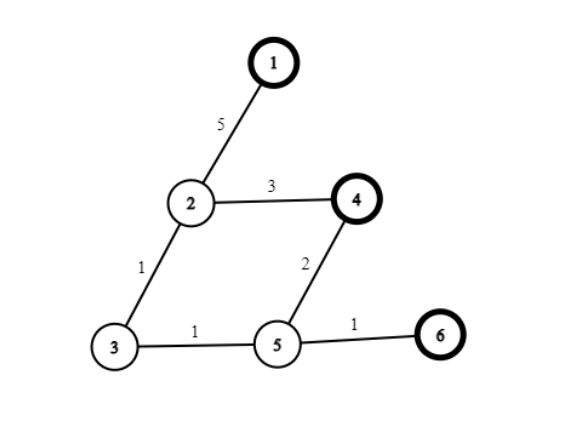
Con cáo và chùm nho
Nộp bàiPoint: 100
Tiếp tục là Châu và câu chuyện hành trình trở thành thợ code của anh ấy. MrTee sau khi thấy Châu đã quá thợ nên đã gửi anh ấy cho thầy Hưng Cao dạy. Thử thách đầu tiên thầy Hưng giao cho Châu là Con cáo và chùm nho (không phải bài nhạc mà các bạn biết). Thử thách có nội dung như sau:
Cho chùm nho có ~N~ quả và ~M~ cành cây, mỗi cành cây nối 2 quả nào đó với nhau. Giữa 2 quả bất kì có thể có nhiều cành cây nối chúng (cây bị down). Cũng có thể có những quả có cành cây nối với chính nó. Đơn giản thì chùm nho là mô hình đồ thị ~N~ đỉnh, ~M~ cạnh.
Các quả nho được đánh số từ ~1~ đến ~N~. Quả thứ ~i~ có độ cao là ~A_i~. Độ dốc giữa cành cây nối giữa 2 quả được tính bằng giá trị tuyệt đối chênh lệch chiều cao giữa 2 quả nho. Ví dụ cành cây nối giữa 2 quả ~x~ và ~y~ sẽ có độ dốc là ~|A_x - A_y|~.
Dù trong nhiều câu chuyện, cáo luôn là phản diện nhưng chúng là loài động vật thông minh. Ai cũng thích động vật thông minh và Châu và thầy Hưng cũng vậy. Để giúp con cáo lấy được chuỗi các quả nho xịn và nhiều nhất, Châu phải thiết kế 1 con đường leo cây siêu nhanh. Xuất phát từ 1 quả nho nào đó, đi đến các quả nho khác với điều kiện các quả nhỏ sau cao hơn quả nho trước, không những thế, độ dốc của cành cây sau cũng phải lớn hơn độ dốc của cành cây trước đó. Nghĩa là, nếu như Châu quyết định chọn một hành trình đi qua các quả nho theo thứ tự ~P_1, P_2, ..., P_k~ thì hành trình đó sẽ phải thỏa mãn tính chất:
~0 < A_{P_2}-A_{P_1} < A_{P_3}-A_{P_2} < ... < A_{P_k}-A_{P_{k-1}}~
Như đã nói, để giúp con cáo, hành trình này cũng phải thỏa mãn việc nó có đi qua nhiều quả nho nhất. Ngoài ra thầy Hưng cũng muốn biết thêm có bao nhiêu cách đi như vậy để còn giật dây hành trình của con cáo.
Vì là thợ đặc cấp nên Châu dễ dàng vượt qua thử thách này và được dạy cho nhiều câu punchline như một phần thưởng.
Liệu bạn có thợ như Châu?
Yêu cầu:
- Tìm đường đi qua nhiều quả nho nhất và thỏa mãn yêu cầu đề bài. Đồng thời tìm xem có bao nhiêu đường đi khác nhau đi qua nhiều quả nho nhất.
Input: dincpath.inp
- Dòng đầu tiên chứa 2 số nguyên ~N~ và ~M~ ~(1 \le N \le 3 * 10 ^ 5, 1 \le M \le 5 * 10^5)~.
- Dòng thứ hai chứa độ cao của ~N~ quả nho là ~N~ số nguyên dương ~A_1, A_2, ..., A_n~ ~(1 \le A_i \le 10^9)~.
- Dòng thứ ~i~ trong số ~M~ dòng tiếp theo chứa cặp số nguyên dương ~(U_i, V_i)~ là chỉ số hai quả nho và là hai đầu của cành cây thứ ~i~ ~(1 \le U_i, V_i \le N)~.
Output: dincpath.out
- Dòng đầu tiên ghi ra một số nguyên là số lượng quả nho của hành trình tìm được.
- Dòng thứ hai ghi ra một số nguyên là phần dư trong phép chia số lượng hành trình khác nhau tìm được cho ~10^9 + 7~.
Subtasks
- Có ~20\%~ số test ứng với ~N \le 20~.
- Có ~20\%~ số test khác ứng với ~N \le 500~.
- Có ~20\%~ số test khác ứng với đồ thị tương ứng là một mạch thẳng (đồ thị dạng cây nhưng mỗi đỉnh chỉ có tối đa 2 cạnh).
- Có ~20\%~ số test khác ứng với ~M = N - 1~, và các đỉnh trong đồ thị liên thông với nhau.
- ~20\%~ còn lại không có giới hạn gì thêm.
Sample Input 1
5 4
1 2 4 4 5
1 2
2 3
3 1
4 5
Sample Output 1
3
1
Watermelon
Nộp bàiPoint: 100
It's not a bug — it's an undocumented feature 😈
Cho một dãy số nguyên ~A~ gồm ~n~ phần tử, được đánh số ~A_1,A_2,...,A_n~.
Ta có một số định nghĩa như sau:
- Trọng số của đoạn con (ở đây là một đoạn con liên tiếp) là tổng các giá trị ~A_i~ trong đoạn.
- Độ cân bằng của dãy ~A~ là trọng số của đoạn con có trọng số lớn nhất trong dãy số.
Bài toán sẽ thật dễ dàng nếu chỉ yêu cầu tính độ cân bằng của dãy ~A~ được cho, vậy nên ~Watermelon~ - người thầy của muôn quả - đã quyết định tăng độ khó bằng cách sau:
- Đầu tiên, thầy đưa ra một dãy số nguyên gồm ~n~ phần tử ~B_1,B_2,...,B_n~.
- Có tối đa ~k~ lượt chỉnh sửa, mỗi lượt bạn được chọn một đoạn con các phần tử từ vị trí thứ ~l~ đến vị trí thứ ~r~ ~(1 \le l \le r \le n)~ và thực hiện phép gán ~A_i = A_i*B_i~ với ~\forall i \in [l,r]~.
Yêu cầu: Đưa ra được độ cân bằng lớn nhất với tối đa ~k~ lượt chỉnh sửa.
Hoa Quả Sơn đã phải bó cành trước bài toán mới này, bạn hãy giúp họ tìm kiếm câu trả lời.
Input: watermelon.inp
- Dòng đầu tiên gồm hai số nguyên ~n~ và ~k~ ~(1 \le n \le 10^5, 0 \le k \le 10)~.
- Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy số nguyên ~A_1, A_2, ..., A_n~ ~(|A_i| \le 1000)~.
- Dòng thứ ba gồm ~n~ số nguyên dương miêu tả dãy số nguyên ~B_1, B_2, ..., B_n~ ~(|B_i| \le 10)~.
Output: watermelon.out
- In ra một số nguyên duy nhất là độ cân bằng lớn nhất tìm được của dãy ~A~ sau khi sử dụng tối đa ~k~ lượt chỉnh sửa.
Scoring:
- Subtask ~1~ ~(15\%)~: ~k = 0~.
- Subtask ~2~ ~(15\%)~: ~k = 1~ và ~n \le 5000~.
- Subtask ~3~ ~(20\%)~: ~k = 1~.
- Subtask ~4~ ~(25\%)~: ~k = 2~.
- Subtask ~5~ ~(25\%)~: Không ràng buộc gì thêm.
Sample Input 1
5 1
-3 4 -5 2 -2
1 -2 -1 2 1
Sample Output 1
13
Sample Input 2
3 0
-4 -10 -8
2 2 -1
Sample Output 2
-4
Explanation:
- Trong ví dụ thứ nhất, cách tối ưu nhất là chọn đoạn ~[3, 4]~ để tác động. Như vậy dãy ~A~ mới là ~[-3, 4, 5, 4, -2]~. Vậy độ cân bằng của dãy này là ~13~.
- Trong ví dụ thứ ~2~, khi ~k = 0~, bạn không thực hiện lượt chỉnh sửa nào và đưa ra độ cân bằng của dãy ~A~ ban đầu là ~-4~.