Bạn được cho một xâu ~S~ có độ dài ~n~ gồm các chữ cái từ a đến z. Nhiệm vụ của bạn là đếm số xâu con liên tiếp mà mỗi cặp kí tự đặc biệt trong xâu con đó có khoảng cách không nhỏ hơn ~k~ (~k \le n~).

Input

• Dòng đầu tiên gồm ba số nguyên dương ~n~, ~m~ và ~k~ ~(1 \le k \le n \le 10^5; 1 \le m \le 10)~ lần lượt là độ dài của xâu ~S~, số lượng kí tự đặc biệt và khoảng cách yêu cầu giữa hai kí tự đặc biệt bất kì.
• Dòng thứ hai chứa xâu ~S~ gồm các chữ cái từ a đến z.
• Dòng cuối cùng gồm ~m~ kí tự là các kí tự đặc biệt, dữ liệu đảm bảo ~k~ kí tự này phân biệt

Output

• Gồm một dòng duy nhất là số lượng xâu con liên tiếp thỏa mãn đề bài

Substask

• ~30\%~ số test: ~1 \le k \le n \le 10^3~.
• ~20\%~ số test: ~1 \le k \le n \le 10^5~, trong xâu chỉ có đúng ~2~ vị trí có kí tự đặc biệt.
• ~50\%~ số test: ~1 \le k \le n \le 10^5~.

Sample Input 1

6 2 2
acbabc
a b

Sample Output 1

10

Explanation 1

Các xâu con thỏa mãn là: a, c, b, a, b, c, ac, acb, cb, bc.

Mít có các que tính có nhiều độ dài và màu sắc. Hôm nay học về hình tam giác nhọn, Mít đã nghĩ ra một bài toán rất độc đáo có liên quan tới tam giác nhọn và các que tính của mình. Mít chia các que tính thành ~N~ bộ, các que tính trong cùng một bộ thì có độ dài bằng nhau nhưng có màu khác nhau. Độ dài của các que tính trong hai bộ bất kì là khác nhau. Mít đố các bạn đếm xem có bao nhiêu tam giác nhọn khác nhau có thể được tạo ra từ ~N~ bộ que tính đó. Chú ý: mỗi cạnh của tam giác được chọn từ một bộ que tính khác nhau tức là sẽ không có tam giác cân và hai tam giác nhọn được gọi là giống nhau khi các cặp cạnh tương ứng bằng nhau và cùng màu, ngược lại là khác nhau.

Yêu cầu: Cho độ dài và số lượng các que tính của ~N~ bộ que tính, hãy lập trình đếm số lượng tam giác nhọn khác nhau có thể tạo ra.

Dữ liệu vào từ tệp văn bản TRIACU.INP:

• Dòng đầu tiên gồm một số nguyên dương ~N~ ~(N ≤ 2000)~ là số bộ que tính;
• ~N~ dòng sau, dòng thứ ~i~ chứa hai số nguyên dương ~L, C~ mô tả độ dài và số lượng que tính của bộ thứ ~i~ ~(1 ≤ i ≤ N~; ~\ L ≤ 10^6~; ~\ C ≤ 10^3)~.

Kết quả ghi ra tệp văn bản TRIACU.OUT:

Một số nguyên duy nhất là số lượng tam giác nhọn khác nhau.

Ràng buộc

• Có ~50\%~ số test ứng với ~N ≤ 200~;
• ~50\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input

4
3 3
4 1
5 2
6 2

Output

4

Giải thích

Có ~4~ tam giác nhọn có thể tạo ra từ bộ que tính thứ ~2, 3, 4~.

Cho dãy số gồm ~n~ số nguyên ~a_1, a_2, …, a_n~ và ~2~ số nguyên không âm ~L, R (L ≤ R)~.

Yêu cầu: Đếm số cặp ~(i, j)~ thỏa mãn điều kiện: ~i ≤ j~ và ~L ≤ |a_i+…+a_j| ≤ R~.

Input

• Dòng đầu tiên chứa ~3~ số nguyên ~n, L, R~ ~(n ≤ 3*10^5 ; 0 ≤ L ≤ R ≤ 10^9)~
• Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2,…, a_n (|a_i|≤ 10^9)~

Output

• Một số nguyên duy nhất là số lượng cặp ~(i, j)~ đếm được.

Subtask

• Subtask 1 (~30\%~ số điểm): ~n \le 10^3~.
• Subtask 2 (~50\%~ số điểm): ~n \le 10^5~ và ~a_i \ge 0~.
• Subtask 3 (~20\%~ số điểm): Không có giới hạn gì thêm.

Sample Test

Input

3 0 1
1 -1 2

Output

4

Sau khi chơi với ngọc chán chê, Tí sắp ~n~ viên ngọc ra một đường thẳng và bắt đầu nhìn ngắm chúng. Tí nhận thấy rằng có không quá ~k~ màu ngọc khác nhau trên bàn và viên ngọc thứ ~i~ từ trái sang thì có màu ~a_i~. Tí muốn chia dãy ngọc thành các đoạn liên tiếp sao cho mỗi đoạn đều có đủ ~k~ màu. Hỏi Tí có bao nhiêu cách chia thỏa mãn như vậy?

Yêu cầu: In số cách chia thỏa mãn sau khi ~\mod 10^9+7~

Input

• Dòng đầu tiên chứa hai số nguyên dương ~n,k~.
• Dòng thứ hai chứa ~n~ số nguyên ~a_1,a_2,...,a_n~.

Output

• Ghi ra một số nguyên là kết quả bài toán.

Constraints

• ~1\leq k\leq n\leq 10^6~
• ~1\leq a_i\leq k~

Scoring

• Subtask ~1~ (~20\%~ số điểm): ~k = 1~.
• Subtask ~2~ (~20\%~ số điểm): ~n\leq 5000~.
• Subtask ~3~ (~20\%~ số điểm): ~n\leq 10^5, k\leq 100~.
• Subtask ~4~ (~40\%~ số điểm): Không có ràng buộc gì thêm.

Example

Sample Input ~1~

5 2
1 2 2 1 2 

Sample Ouput ~1~

3

Explanation

Có ~3~ cách chia như sau: ~(1\ 2) | (2\ 1\ 2), (1\ 2\ 2) | (1\ 2)~, hoặc ~(1\ 2\ 2\ 1\ 2)~.

Hè đã tới, ~mrtee~ muốn cho các học sinh của mình vận động một chút. Thầy đã lập ra một cuộc thi nhảy xa, tuy nhiên điều luật của nó thì rất lạ.

Nếu chiếu trên trục ~OX~, đường nhảy sẽ bắt đầu từ điểm ~1~ và kết thúc tại điểm ~n~. Bạn sẽ xuất phát từ điểm ~0~ và được nhảy bao nhiêu lượt tùy thích, miễn là không ra khỏi phạm vi ~[1,n]~. Tuy nhiên, mỗi lượt bạn phải nhảy một quãng đường nguyên dương và ở lần nhảy thứ ~i~, bạn phải nhảy một quãng đường có độ chia hết cho ~k+i-1~. Tất nhiên, bạn sẽ được cung cấp trước ~2~ giá trị ~n~ và ~k~.

Là một ~coder~ yêu thích toán học, bạn không quan tâm tới việc thắng thua trong cuộc thi này lắm, mà chỉ hứng thú với việc đếm xem với mỗi vị trí ~i~ thuộc đoạn ~[1,n]~, có bao nhiêu cách nhảy khác nhau từ điểm xuất phát tới đó.

Hãy thử lập trình và giải đáp câu hỏi ấy!

Input

• Gồm một dòng chứa hai số nguyên dương ~n, k~.
  
  

Output

• In ra ~n~ số nguyên, số thứ ~i~ là số cách để nhảy từ điểm ~0~ tới điểm ~i~, vì kết quả có thể rất lớn nên hãy lấy phần dư với modulo ~10^9+7~.
  
  

Constraints

• ~1 \le k \le n \le 2*10^5~
  
  

Subtasks

• ~35\%~ số điểm: ~n \le 300~.
• ~40\%~ số điểm: ~n \le 4000~.
• ~25\%~ số điểm: ~n \le 2*10^5~.
  
  

Sample Test 1

Input:

12 1

Output:

1 1 2 2 3 4 5 6 8 10 12 15

Sample Test 2

Input:

15 3

Output:

0 0 1 0 0 1 1 0 1 1 1 2 1 1 3

Giải thích

• Ở ví dụ ~1~, các cách để đến điểm ~6~ là ~[0,6],[0,4,6],[0,2,6],[0,1,3,6]~.
• Ở ví dụ ~2~, các cách để đến điểm ~15~ là ~[0,15],[0,3,12],[0,6,10,15]~

Alice vừa mới lạc vào một vùng đất rất kì lạ tên là "Bruhderland". Đây là một vùng đất lai giữa "Wonderland" và "Borderland", nơi có phép màu và cả những trò chơi sinh tử.

Bruhderland được biểu diễn bằng một ma trận ~n \times m~, với ô ~(i,j)~ là một trong các kí tự sau:

• .: có nghĩa là ô đất trống, có thể đi vào.
• *: có nghĩa là ô có một tảng đá, không thể đi vào.
• A: có nghĩa là có một trò chơi với độ khó ~A~ ở ô này, Alice rất giỏi nên sẽ có thể vượt qua trò chơi, nhưng sẽ mất ~1~ sức lực.
• B: có nghĩa là có một trò chơi với độ khó ~B~ ở ô này, Alice vẫn sẽ có thể vượt qua trò chơi, nhưng sẽ mất ~2~ sức lực.

Giả sử, Alice đang ở ô ~(i,j)~, cô có thể đi sang ~4~ ô kề cạnh nếu như ô đó không vượt qua ngoài bảng và không chứa tảng đá nào. Như đã nói, Bruhderland có cả yếu tố phép màu, vậy nên khi vào đây, cô đã học được cách đọc thần chú để phá hủy một tảng đá bất kì mà không mất sức lực nào (nghĩa là có thể đi vào ô chứa tảng đá vừa bị phá hủy), tuy nhiên do năng lực giới hạn, Alice chỉ có thể đọc thần chú ~k~ lần mà thôi.

Alice đang ở ô ~(1,1)~, để thoát ra khỏi Bruhderland, cô sẽ cần đến ô ~(n,m)~. Tuy nhiên, do khá lười tham gia vào các trò chơi, Alice muốn thoát ra khỏi Bruhderland sao cho tốn ít sức lực nhất.

Quan trọng: Dữ liệu đảm bảo kết quả không quá ~2500~.

Input: BRUHDERLAND.INP

• Dòng đầu tiên ghi ~3~ số nguyên dương ~n,m,k~ ~(1 \le n,m \le 1000, 0 \le k \le 5)~.
• ~n~ dòng sau, dòng thứ ~i~ gồm một xâu kí tự độ dài ~m~ miêu tả hàng thứ ~i~ của ma trận.
• Dữ liệu đảm bảo ô ~(1,1)~ là kí tự . và luôn tồn tại cách đi từ ~(1,1)~ tới ~(n,m)~ nếu sử dụng thần chú một cách hợp lý.

Output: BRUHDERLAND.OUT

• In ra một số nguyên dương là số sức lực ít nhất cần tiêu tốn để đến được ô ~(n,m)~.

Scoring:

• Subtask ~1~ ~(10\%)~: ~ n\times m \le 10^5~, ~k = 0~ và các ô khác ô ~(1,1)~ chỉ gồm kí tự A
• Subtask ~2~ ~(15\%)~: ~ n\times m \le 10^5~, ~k = 0~ và các ô khác ô ~(1,1)~ không có kí tự B và ..
• Subtask ~3~ ~(10\%)~: ~k = 0~ và các ô khác ô ~(1,1)~ không có kí tự B.
• Subtask ~4~ ~(10\%)~: Các ô khác ô ~(1,1)~ không có kí tự B.
• Subtask ~5~ ~(15\%)~: ~n \times m \le 10^5~ và ~k = 0~.
• Subtask ~6~ ~(20\%)~: ~n \times m \le 10^5~.
• Subtask ~7~ ~(20\%)~: Không có giới hạn gì thêm.

Sample Input 1

4 4 0
.AAA
AAAA
AAAA
AAAA

Sample Output 1

6

Sample Input 2

5 4 0
.AAA
***A
AAAA
A***
AAAA

Sample Output 2

13

Sample Input 3

5 4 0
.AAA
***B
AAAA
A**B
BAAA

Sample Output 3

9

Sample Input 4

5 4 2
.BAA
****
AABA
A***
BABA

Sample Output 4

6

Một xí nghiệp có một robot dùng để xếp các sản phẩm vào các thùng. Mọi thùng đều có dung tích như nhau. Có đúng hai thùng đang mở sẵn để robot xếp các sản phẩm vào. Mỗi thùng bất kỳ đều chứa được số sản phẩm mà tổng dung tích của chúng không vượt quá dung tích của thùng. Robot có thể thực hiện các thao tác sau:

• Đưa một sản phẩm hiện tại trên dãy băng vào thùng ~1~,
• Đưa một sản phẩm hiện tại trên dãy băng vào thùng ~2~,
• Đóng thùng ~1~ và mở một thùng mới thay thế cho thùng ~1~,
• Đóng thùng ~2~ và mở một thùng mới thay thế cho thùng ~2~.

Các thao tác 1, 2 chỉ có thể thực hiện nếu tổng dung tích của sản phẩm cho vào và các sản phẩm đã có trong thùng không vượt quá dung tích của thùng.

Yêu cầu: Cho biết dung tích mỗi thùng là ~𝑊~, dung tích của ~𝑛 sản~ phẩm trên dãy băng theo thứ tự xuất hiện là ~𝑎_1, 𝑎_2, . . . , 𝑎_𝑛~ , hãy tìm số thùng ít nhất để có thể cho ~𝑛~ sản phẩm vào thùng.

Input

• Dòng thứ nhất là hai số nguyên ~𝑊~ và ~𝑛~;
• Dòng tiếp theo chứa các số mô tả các số ~𝑎_1, 𝑎_2, … , 𝑎_𝑛~.

Output

• Gồm một số duy nhất là số thùng ít nhất cần dùng.

Input

8 6
4 2 5 3 5 4

Output

3

Giải thích

• Đưa ~1~ vào thùng ~1~
• Đưa ~2~ ~3~ ~4~ ~5~ vào thùng ~2~ (cần mở thêm một thùng)
• Đưa ~6~ vào thùng ~1~ (vẫn còn đủ chỗ, không cần mở thêm)

Ràng buộc

• Subtask 1 [10 tests] ~𝑊 ≤ 10^9 ; 𝑛 ≤ 20~
• Subtask 2 [10 tests] ~1 ≤ 𝑎_𝑖 ≤ 2; 𝑊 = 100; 𝑛 ≤ 10^6~
• Subtask 3 [10 tests] ~𝑊 ≤ 30; 𝑛 ≤ 10000~
• Subtask 4 [10 tests] ~𝑊 ≤ 5000; 𝑛 ≤ 100~
• Subtask 5 [10 tests] ~𝑊 ≤ 5000 ; 𝑛 ≤ 10000~

Vì Gojo Satoru quá yếu, nên một ngày đẹp trời Sukuna đã rủ Chau solo bành trướng lãnh địa.

Cả ~2~ solo trên mảnh đất là một bảng hình chữ nhật ~A~, có diện tích ~N \times M~ với ~N~ hàng và ~M~ cột. Kí hiệu ~(i, j)~ là ô nằm trên hàng thứ ~i~, cột thứ ~j~ với các hàng được đánh số từ trên xuống dưới theo thự từ ~1~ đến ~N~, các cột được đánh số từ trái sang phải theo thự từ ~1~ đến ~M~.

Sukuna và Chau đã bành trướng lên lãnh địa này và vẽ ra ~2~ vùng lãnh địa của mình. Trên bảng ~A~, ta kí hiệu ~A (i , j) = 1~ nếu ô đó chứa biên của phần lãnh địa Chau, ~A (i, j) = 2~ nếu ô đó chứa biên của phần lãnh địa của Sukuna, ~A (i, j) = 3~ nếu nó chứa biên của phần lãnh địa của cả hai người, còn ~A (i, j) = 0~ nếu nó là đất trống. Đảm bảo biên của mỗi lãnh địa tạo thành một vòng khép kín. (Biên tức là vòng ngoài của lãnh địa).

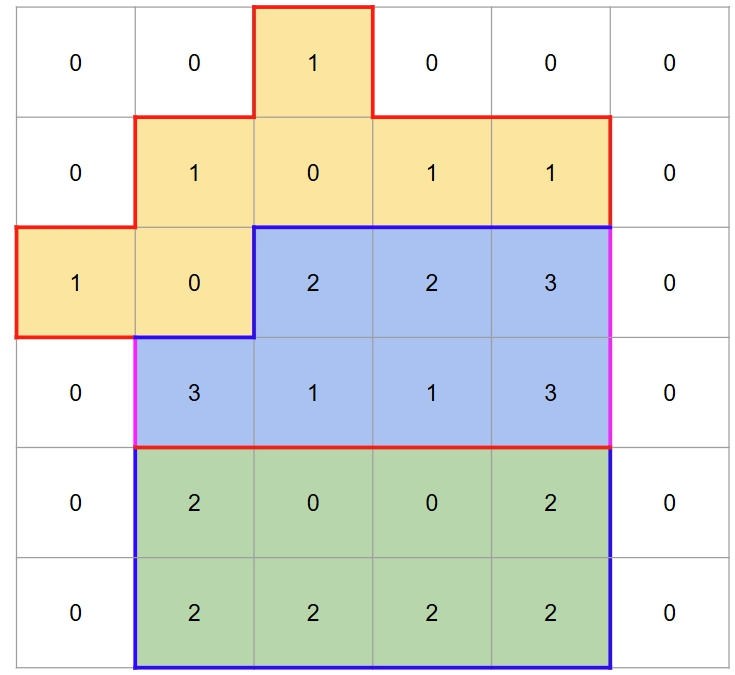
Hình trên là minh họa cho test ví dụ 1.

• Viền màu đỏ là biên của lãnh địa của Chau. Viền màu xanh là biên lãnh địa của Sukuna. Viền màu tím là biên lãnh địa của cả 2.
• Các ô màu cam là các ô thuộc chỉ thuộc lãnh địa của Chau. Các ô màu xanh lá là các ô chỉ thuộc lãnh địa của Sukuna. Các ô màu xanh dương là các ô thuộc lãnh địa của cả hai.

Vì mải dùng Thuật Thức nên Chau không thể dùng Thuật Toán, Chau muốn các bạn tính hộ xem có bao nhiêu ô thuộc cả ~2~ lãnh địa

Yêu cầu: In ra số ô thuộc cả ~2~ lãnh địa.

Input

• Dòng đầu tiên là 2 số tự nhiên ~N, M~ ~(N, M\leq 1000)~ là số hàng và cột của bảng ~A~.
• ~N~ dòng tiếp theo, môi dòng là một hàng của bảng ~A~ và có ~M~ số nguyên không âm nhỏ hơn hoặc bằng 3. Ý nghĩa giá trị của mỗi số nguyên không âm đã nếu ở đề bài ở trên.

Output

• In ra một số nguyên không âm là kết quả của bài toán.

Subtask

• Subtask ~1~ (~25\%~ số điểm): ~N = 1~ .
• Subtask ~2~ (~25\%~ số điểm): ~N, M\leq 100~ và các ô biên của 2 lãnh địa trùng nhau.
• Subtask ~3~ (~25\%~ số điểm): ~N, M\leq 100~.
• Subtask ~4~ (~25\%~ số điểm): Không có ràng buộc gì thêm.

Sample Input 1

6 6
0 0 1 0 0 0
0 1 0 1 1 0
1 0 2 2 3 0
0 3 1 1 3 0
0 2 0 0 2 0
0 2 2 2 2 0

Sample Output 1

7

Cho đồ thị đầy đủ vô hướng có trọng số (nghĩa là đồ thị gồm ~\frac{n*(n-1)}{2}~ cạnh phân biệt), trong đó có ~m~ cạnh có trọng số là ~1~, các cạnh còn lại có trọng số là ~0~.

Hãy tìm cây khung nhỏ nhất của đồ thị này.

Input:

• Dòng đầu tiên ghi số nguyên ~n~ và ~m~ ~(1 \le n \le 2*10^5, 1 \le m \le min(4*10^5,\frac{n*(n-1)}{2}))~
• ~m~ dòng tiếp theo, mỗi dòng gồm ~2~ số nguyên ~u_i,v_i~ ~(1 \le u_i, v_i \le n, u_i \neq v_i)~ - miêu tả cạnh ~(u_i,v_i)~ có trọng số là ~1~.

Output:

• Trọng số của cây khung nhỏ nhất của đồ thị.

Constraints:

• Có ~50\%~ số test ứng với ~n \le 2*10^3~
• ~50\%~ số test còn lại không có điều kiện gì thêm.

Ví dụ

Input 1

6 11
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6

Output 1

2

Input 2

3 0

Output 2

0

Vùng đất Midland đang có chiến tranh tàn khốc. Bạn đang ở vùng giao tranh, và giờ phải gửi tài liệu mật từ đơn vì tới cho sở chỉ huy. Vùng này được biểu diễn dưới dạng một ma trận ~n \times m~, ô ở hàng ~i~ cột ~j~ được gọi là ô ~(i,j)~.

Công việc này chưa bao giờ là dễ dàng. Một vài ô đã bị địch cài bom và không biết khi nào sẽ phát nổ. Bạn chỉ biết rằng loại bom này có sức công phá là ~r~, có nghĩa là nếu bom ở ô ~(i,j)~, khi nó phát nổ thì các ô ~(u,v)~ thỏa mãn ~|i-u| + |j-v| \le r~ sẽ bị tàn phá (ô ~(i,j)~ và ~(u,v)~ đều nằm trong bảng). Những ô ~(u,v)~ như vậy gọi là những ô bị ảnh hưởng bởi bom.

Đây là tài liệu mật, tất nhiên chỉ huy của bạn không muốn nhận một sự rủi ro nào, vậy nên bạn được lệnh phải tìm một đường đi ngắn nhất từ đơn vị tới sở chỉ huy sao cho không được đi qua ô nào bị ảnh hưởng bởi bom. Biết rằng bạn có thể đi sang ~4~ ô kề cạnh với ô đang đứng và mỗi ô ~(i,j)~ sẽ được miêu tả bằng một kí tự như sau:

• ~c(i,j) =~ ., nếu đây là một ô bình thường có thể đi.
• ~c(i,j) =~ *, đây là vùng nguy hiểm tuyệt đối không được đi vào.
• ~c(i,j) =~ +, đây là ô có bom, như đã nói, các ô nằm cách ô này khoảng cách không quá ~r~ (kể cả chính nó) sẽ không thể đi vào.
• ~c(i,j) =~ S, đây là đơn vị của bạn, sẽ chỉ có duy nhất một ô thế này xuất hiện.
• ~c(i,j) =~ T, đây là sở chỉ huy, sẽ chỉ có duy nhất một ô thế này xuất hiện.
  
  

Input

• Dòng đầu tiên gồm ~3~ số nguyên ~n,m,r~, miêu tả kích thước bảng và vùng ảnh hưởng của bom.
• ~n~ dòng sau, mỗi dòng gồm ~m~ kí tự miêu tả vùng đất.
• Dữ liệu luôn đảm bảo ô chứa kí tự ~S~ và ~T~ không bị ảnh hưởng bởi ô chứa bom nào.
  
  

Output

• In ra một dòng là đường đi ngắn nhất từ đơn vị tới sở chỉ huy sao cho không được đi qua ô nào bị ảnh hưởng bởi bom. Nếu không có một đường đi nào như vậy, in ra ~-1~.
  
  

Constraints

• ~1 \le n,m \le 1000~
• ~0 \le r \le 1000~
  
  

Subtasks

• ~20\%~ số điểm: Không có ô nào có ~c(i,j) = *~ hoặc ~c(i,j) = +~.
• ~20\%~ số điểm: ~r = 0~.
• ~30\%~ số điểm: ~n,m \le 100~.
• ~30\%~ số điểm: Không có ràng buộc gì thêm.
  
  

Sample Test 1

Input:

3 4 1
S...
....
...T

Output:

5

Sample Test 2

Input:

3 4 0
S.+T
*.*.
*...

Output:

7

Sample Test 3

Input:

4 4 1
S..*
*...
+.*.
.T..

Output:

8

Cho một đồ thị vô hướng gồm ~n~ đỉnh ~m~ cạnh. Cạnh ~i~ nối giữa đỉnh ~u_i~ và ~v_i~ và có kí tự ~c_i~ được viết lên trên nó.

Hãy tìm một đường đi từ ~1~ đến ~n~ ngắn nhất mà sau khi viết các kí tự có được khi đi qua các cạnh là một xâu palindrome. Nếu không tồn tại bất kì đường đi nào thỏa mãn là palindrome, in ra ~-1~.

Lưu ý: Đồ thị có thể tồn tại khuyên và cạnh lặp, các đỉnh và cạnh có thể đi qua lại nhiều lần.

Input

• Dòng đầu tiên gồm hai số nguyên dương ~n, m~ ~(1 \le n, m \le 1000)~.
• ~m~ dòng tiếp theo, mỗi dòng gồm ~u_i, v_i, c_i~ mô tả cạnh thứ ~i~ của đồ thị.

Output

• Nếu tồn tại một đường đi tạo ra xâu palindrome, in ra độ dài ngắn nhất có thể. Nếu không, in ra ~-1~.

Sample Input 1

4 5
1 1 a
1 2 a
2 3 a
3 4 b
4 4 a

Sample Output 1

5

Explanation 1

Đi qua các cạnh ~2, 3, 4, 5, 5~, ta nhận được xâu aabaa.

Sample Input 2

3 4
1 1 a
1 2 a
2 3 b
3 3 b

Sample Output 2

-1