Em hãy tưởng tượng các chữ số từ trái sang phải của số nguyên ~N~ được xếp trên một vòng tròn lần lượt theo chiều kim đồng hồ. Ví dụ, số ~197~ được bố trí vòng tròn như hình:

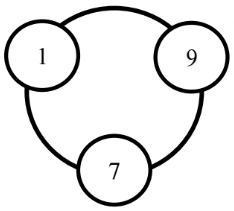
Khi đọc các chữ số xuôi theo chiều kim dồng hồ ta được các số ~197~, ~971~ và ~719~. Điều thú vị ở ví dụ này đó là các số đọc theo chiều kim đồng hồ đều là những số nguyên tố. Chính vì vậy, số ~197~ được gọi là số nguyên tố vòng quanh (hay vòng tròn).

Có tất cả ~13~ số nguyên tố vòng tròn như vậy dưới ~100~: ~2~, ~3~, ~5~, ~7~, ~11~, ~13~, ~17~, ~31~, ~37~, ~71~, ~73~, ~79~, ~97~.

Hỏi có bao nhiêu số nguyên tố vòng tròn nhỏ hơn ~N~ cho trước?

Input

• Gồm một dòng duy nhất chứa số nguyên dương ~N~ (~1 \leq N \leq 10^6~).

Output

• In ra một số duy nhất là số lượng các số nguyên tố vòng tròn nhỏ hơn ~N~.

Sample Test

Input:

100

Output:

13

Người ta có câu: "Nhỏ không học, lớn lên làm nhà báo" dùng để châm chọc những người làm báo gian dối, đưa những tin tức sai sự thật để gây hoang mang cho độc giả. Điều này đã gây ra rất nhiều áp lực cho những nhà báo chân chính. Cũng chính vì vậy mà toà soạn báo Liems có quy trình tuyển chọn nhà báo hết sức gắt gao.

Có ~n~ nhà báo muốn ứng tuyển vào toà soạn Liems. Nhà báo thứ ~i~ có điểm uy tín ~a_i~ và đã viết tổng cộng ~b_i~ bài báo trong sự nghiệp. Khi đó, điểm uy tín trung bình của nhà báo này là ~\displaystyle\frac{a_i}{b_i}~ ~(1\le i\le n)~.

Liems chỉ tuyển nhà báo theo ngày, nghĩa là một nhà báo chỉ được làm trong một ngày. Ngoài ra, để đảm bảo rằng những bài báo trở nên đáng tin cậy hơn theo thời gian, mỗi ngày điểm uy tín trung bình của nhà báo trong ngày đó phải cao hơn điểm uy tín trung bình của tất cả các nhà báo những ngày trước đó.

Tuy nhiên, đôi lúc toà soạn muốn tăng KPI, khi đó toà soạn có thể chọn một nhà báo ~k~ tuỳ ý và "hack" điểm uy tín trung bình của nhà báo đó thành ~\displaystyle\frac{b_k}{a_k}~ ~(1\le k\le n)~.

Khi xét từng nhà báo từ ~1~ đến ~n~, toà soạn chỉ có một trong hai lựa chọn: loại nhà báo đó hoặc cho nhà báo đó làm vào ngày tiếp theo so với những nhà báo được chọn trước đó. Nói cách khác, giả sử ~i~ và ~j~ là hai nhà báo được chọn với ~1\le i\lt j\le n~ thì nhà báo ~i~ phải làm trước nhà báo ~j~.

Hãy tìm số ngày tối đa mà toà soạn Liems có thể hoạt động.

Input

• Dòng đầu tiên chứa hai số nguyên ~n, w~ ~(1\le n\le 10^3; \ 0\le w\le 1)~. Nếu ~w=1~ thì có nghĩa toà soạn đó sẽ "hack" điểm uy tín trung bình của một nhà báo tuỳ ý;
• Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa hai số nguyên dương ~a_i, b_i~ ~(1\le a_i, b_i\le 10^9; \ 1\le i\le n)~.

Output

Một số nguyên là số ngày tối đa toà soạn có thể hoạt động.

Ví dụ

Input

4 0
5 1
1 3
3 2
1 2

Output

2

Giải thích

Có nhiều cách chọn các nhà báo thoả mãn, ví dụ như hai nhà báo ~(2, 4)~. Có thể thấy, chỉ có thể chọn tối đa hai nhà báo nên toà soạn chỉ có thể hoạt động trong nhiều nhất ~2~ ngày.

Input

4 1
5 1
1 3
3 2
1 2

Output

3

Giải thích

Toà soạn có thể "hack" điểm uy tín của nhà báo thứ ~4~. Khi đó, có thể chọn tối đa ~3~ nhà báo là ~(2, 3, 4)~, tương ứng với tối đa ~3~ ngày mà toà soạn có thể hoạt động.

Scoring

• Subtask ~1 \ (25\%)~: ~n\le 10; \ w=0~;
• Subtask ~2 \ (25\%)~: ~n\le 10; \ w=1~;
• Subtask ~3 \ (25\%)~: ~w=0~;
• Subtask ~4 \ (25\%)~: Không có ràng buộc gì thêm.