Trong một đất nước có ~𝑁~ thành phố được đánh số từ ~1~ đến ~𝑁~, các thành phố được nối với nhau bởi ~𝑁 - 1~ con đường hai chiều, đảm bảo hai thành phố bất kì có thể đi được đến nhau. Có ~𝑀~ thành phố đang có dịch bệnh. Người ta muốn chọn thành phố để xây dựng bệnh viện dã chiến sao cho: chỉ số an toàn từ thành phố đó đến thành phố đang có dịch bệnh bất kì đều không lớn hơn ~𝐾~ ~(𝐾~ là một số cho trước và chỉ số an toàn giữa hai thành phố ~X~ và ~𝑌~ được tính bằng tổng số con đường trên đường đi từ ~𝑋~ đến ~𝑌)~.

Yêu cầu: Em hãy lập trình để tính xem có thể xây dựng bệnh viện dã chiến ở bao nhiêu thành phố?

Dữ liệu nhập vào từ file văn bản BV.INP:

• Dòng đầu tiên gồm ba số nguyên dương ~𝑁, 𝑀, 𝐾~ ~(1 ≤ 𝐾 ≤ 𝑀 ≤ 𝑁 ≤ 10^5)~ mô tả số lượng thành phố, số lượng thành phố đang có dịch bệnh và số ~K;~
• ~𝑁 - 1~ dòng sau gồm hai số nguyên ~𝑢~ và ~𝑣~ mô tả có con đường nối hai thành phố thứ ~𝑢~ và thứ ~𝑣~ ~(1 ≤ 𝑢, 𝑣 ≤ 𝑁);~
• Dòng tiếp theo gồm ~𝑀~ số nguyên ~𝑥~ mô tả những thành phố đang có dịch bệnh ~(1 ≤ 𝑥 ≤ 𝑁)~.

Kết quả ghi ra file văn bản BV.OUT:

Gồm một số nguyên duy nhất là số thành phố có thể thoả mãn để xây dựng bệnh viện dã chiến (thành phố đang có dịch bệnh cũng có thể xây dựng bệnh viện dã chiến).

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 500;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10^4;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: mỗi thành phố chỉ có đường đi trực tiếp đến tối đa hai thành phố khác~;~
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

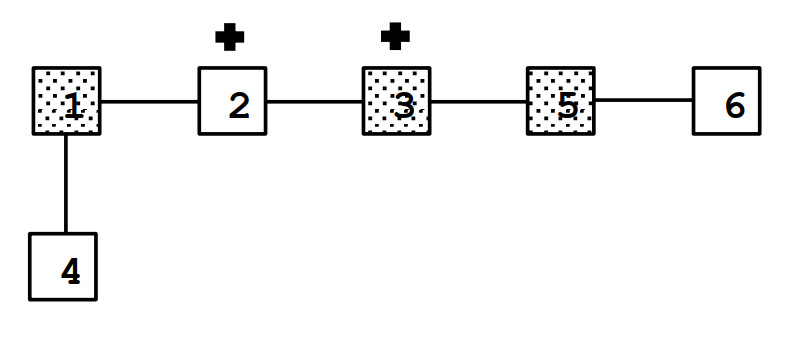
6 2 2
1 2
3 2
3 5
4 2
5 6
1 3

Output

4

Giải thích: Có ~4~ thành phố có thể xây dựng bệnh viện dã chiến: ~1, 2, 3, 4~.

Input

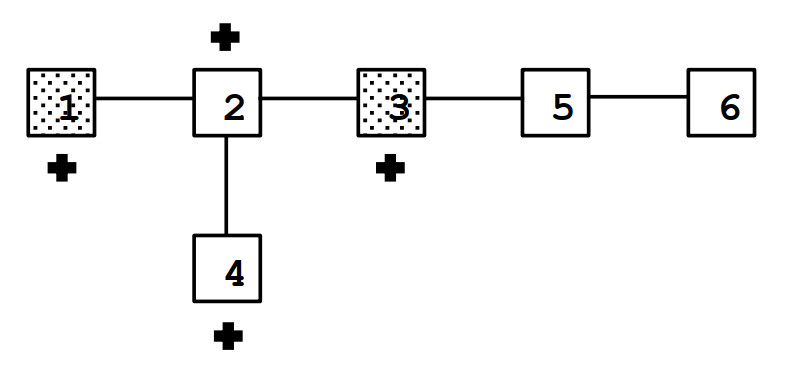
6 3 2
1 2
3 2
3 5
4 1
5 6
1 3 5

Output

2

Giải thích: Có ~2~ thành phố có thể xây dựng bệnh viện dã chiến: ~2, 3~. Thành phố ~4~ không xây dựng được bệnh viện dã chiến vì chỉ số an toàn từ thành phố ~4~ đến thành phố đang dịch bệnh ~5~ là ~4~.