Cho bàn cờ kích thước ~N \times N~ gồm ~N~ hàng ngang được đánh số từ ~1~ đến ~N~ từ dưới lên trên và ~N~ cột dọc được đánh số từ ~1~ đến ~N~ từ trái qua phải (Hình ~1~). Ô nằm trên giao của hàng ~i~ và cột ~j~ của bàn cờ ký hiệu là ô ~(i, j)~. Quân Mã có khả năng khống chế tất cả các ô ở đỉnh đối diện trên đường chéo của hình chữ nhật kích thước ~2 \times 3~ (Hình ~2~). Trên ~K~ ô của bàn cờ có ghi các giá trị thưởng, các ô này ta sẽ gọi là ô thưởng. Ô thưởng thứ ~i~ ghi số nguyên dương ~C_i~ (~i = 1, 2, ... , K~).

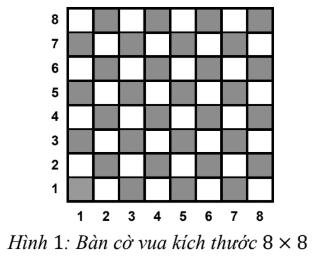
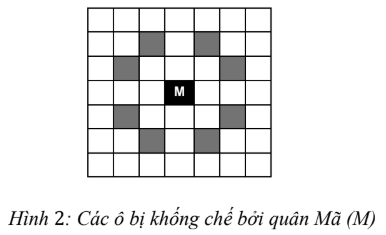
Yêu cầu: Tìm một vị trí ô không có thưởng trên bàn cờ để đặt quân Mã sao cho tổng các giá trị các ô thưởng bị quân Mã này khống chế là lớn nhất.

Dữ liệu: Vào từ thiết bị vào chuẩn có cấu trúc như sau:

• Dòng đầu tiên chứa hai số nguyên dương ~N~ và ~K~ (~N \le 10^9,K < min(N^2, 10^6)~);
• Dòng thứ ~i~ (~i = 1, 2, ... , K~) trong số ~K~ dòng tiếp theo ghi ba số nguyên dương ~u_i, v_i, C_i~ cho biết ô ~(u_i, v_i)~ là ô có thưởng với giá trị là ~C_i~ (~C_i \le 10^9~).

Kết quả: Ghi ra thiết bị ra chuẩn gồm một dòng chứa một số nguyên là tổng các giá trị các ô thưởng bị quân Mã khống chế là lớn nhất.

Ví dụ:

Dữ liệu	Kết quả	Giải thích
5 4 5 1 3 4 4 5 2 5 1 1 4 6	8	Đặt quân Mã ở vị trí ~(3, 2)~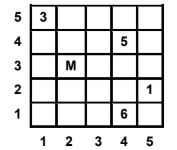

Ràng buộc:

• Có ~60\%~ số test tương ứng với ~60\%~ số điểm có ~N \le 10^3~;
• ~40\%~ số test còn lại tương ứng với ~40\%~ số điểm không có ràng buộc gì thêm.