Trò chơi diễn ra trên bảng ô vuông kích thước ~m \times n~, các hàng của bảng được đánh số từ ~1~ đến ~m~ (từ trên xuống dưới), các cột của bảng được đánh số từ ~1~ đến ~n~ (từ trái sang phải). Ô giao giữa hàng ~i~ và cột ~j~ được gọi là ô ~(i, j)~. Trên bảng có ~k~ ô có chứa quà. Người chơi xuất phát tại ô ~(1, 1)~ và di chuyển đến ô ~(m, n)~. Mỗi bước đi, người chơi chỉ có thể đi sang ô kề cạnh ở cột bên phải hoặc đi xuống ô kề cạnh ở dòng dưới. Khi đi vào ô chứa quà, người chơi sẽ được nhận quà tại ô đó. Nhiệm vụ của người chơi là tìm cách đi để nhận được nhiều quà nhất.

Một ô chứa quà được gọi là vị trí quan trọng, nếu bỏ quà tại ô đó thì số lượng quà nhiều nhất mà người chơi thu được bị giảm đi ~1~.

Yêu cầu: Cho ~m, n~ là kích thước của bảng và vị trí ~k~ ô đặt quà. Hãy đếm số lượng ô được gọi là quan trọng.

Dữ liệu: Vào từ thiết bị vào chuẩn gồm hai dòng:

• Dòng đầu chứa ba số nguyên ~m, n, k~ (~m, n \le 10^9; k \le 10^5~);
• ~k~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~x, y~ (~1 \le x \le m; 1 \le y \le n~) mô tả vị trí các ô chứa quà, các ô phân biệt (không có nhiều hơn một quà ở cùng một ô).

Kết quả: Ghi ra thiết bị ra chuẩn một số nguyên duy nhất là số lượng ô được gọi là vị trí quan trọng.

Ví dụ:

Dữ liệu	Kết quả	Giải thích
4 5 3 2 1 1 5 4 4	2	Có hai vị trí quan trọng là ô (2, 1) và ô (4, 4) .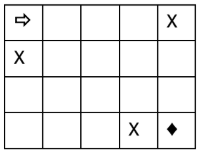

Ràng buộc:

• Có ~40\%~ số test tương ứng với ~40\%~ số điểm có ~m, n \le 100; k \le 100~;
• ~30\%~ số test khác tương ứng với ~30\%~ số điểm có ~m, n \le 10^6; k \le 1000~;
• ~30\%~ số test còn lại tương ứng với ~30\%~ số điểm không có ràng buộc gì thêm.