Đan Phượng 25 - 1
Kiểm tra Số nguyên tố
Nộp bàiPoint: 1
Trong ngày thực tập đầu tiên, thầy Hải có một câu đố nho nhỏ cho các học sinh của mình. Cho một số nguyên ~n~, hãy kiểm tra ~n~ có phải là số nguyên tố hay không?
Số nguyên tố là số tự nhiên lớn hơn 1 chỉ có hai ước số dương phân biệt là 1 và chính nó.
Input:
- Gồm một dòng duy nhất là số nguyên ~n~ (~|n| \le 10^{12})~
Output:
- In ra
YESnếu ~n~ là số nguyên tố. Ngược lại in raNO.
Sample Tests
Input
9
Output
NO
Input
7
Output
YES
Sàng nguyên tố
Nộp bàiPoint: 1
Bạn có một số nguyên dương ~N~. Nhiệm vụ của bạn là xuất ra tất cả các số nguyên tố từ ~1~ tới ~N~.
Input
- Gồm một dòng duy nhất chứa số nguyên ~N~ (~N \leq 10^6)~.
Output
- Xuất ra tất cả các số nguyên tố từ ~1~ tới ~N~ trên cùng một dòng và cách nhau một dấu cách.
Sample Tests
Input
10
Output
2 3 5 7
Prime Factor 1
Nộp bàiPoint: 1
Cho số nguyên dương ~n~, hãy phân tích ~n~ dưới dạng thừa số nguyên tố.
https://www.facebook.com/nguyen.uc.huy.97646/
Input
- Gồm số nguyên dương ~n~.
Output
- In ra theo ví dụ.
Constraints
- ~1 \le n \le 10^{12}~.
Sample Input 1
12
Sample Output 1
2 2
3 1
Giải thích
~12 = 2^2 \times 3^1~
Rút gọn
Nộp bàiPoint: 1
Cho một phân số ~\frac a b~. Hãy rút gọn phân số này.
Input
- Gồm một dòng chứa ~2~ số nguyên là tử số ~a~ và mẫu số ~b~. (~0 \leq a \leq 10^9, 1 \leq b \leq 10^9~).
Output
- In ra phân số sau khi đã rút gọn sử dụng dấu
/.
Sample Tests
| Input | Output |
|---|---|
| 6 9 | 2/3 |
| 1 5 | 1/5 |
Prime Factor 2
Nộp bàiPoint: 1
Cho ~q~ truy vấn, mỗi truy vấn gồm một số nguyên dương ~n~.
Với mỗi truy vấn, hãy phân tích ~n~ dưới dạng thừa số nguyên tố.
Input
- Dòng đầu gồm số nguyên dương ~q~ miêu tả số truy vấn.
- ~q~ dòng sau, mỗi dòng gồm số nguyên dương ~n~.
Output
- In ra theo ví dụ.
Constraints
- ~1 \leq q \leq 2 \times 10^5~.
- ~1 \le n \leq 10^6~.
Sample Input 1
3
12
24
9
Sample Output 1
2 2
3 1
2 3
3 1
3 2
Giải thích
~12 = 2^2 \times 3^1~
~24 = 2^3 \times 3^1~
~9 = 3^2 ~
Số nguyên tố vòng
Nộp bàiPoint: 1
Em hãy tưởng tượng các chữ số từ trái sang phải của số nguyên ~N~ được xếp trên một vòng tròn lần lượt theo chiều kim đồng hồ. Ví dụ, số ~197~ được bố trí vòng tròn như hình:
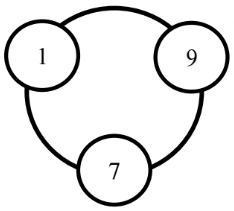
Khi đọc các chữ số xuôi theo chiều kim dồng hồ ta được các số ~197~, ~971~ và ~719~. Điều thú vị ở ví dụ này đó là các số đọc theo chiều kim đồng hồ đều là những số nguyên tố. Chính vì vậy, số ~197~ được gọi là số nguyên tố vòng quanh (hay vòng tròn).
Có tất cả ~13~ số nguyên tố vòng tròn như vậy dưới ~100~: ~2~, ~3~, ~5~, ~7~, ~11~, ~13~, ~17~, ~31~, ~37~, ~71~, ~73~, ~79~, ~97~.
Hỏi có bao nhiêu số nguyên tố vòng tròn nhỏ hơn ~N~ cho trước?
Input
- Gồm một dòng duy nhất chứa số nguyên dương ~N~ (~1 \leq N \leq 10^6~).
Output
- In ra một số duy nhất là số lượng các số nguyên tố vòng tròn nhỏ hơn ~N~.
Sample Test
Input:
100
Output:
13
Khoảng cách
Nộp bàiPoint: 1
Với hai số nguyên dương ~a, b~, ta định nghĩa khoảng cách giữa ~a~ và ~b~ là số phép nhân với một số nguyên tố hoặc chia hết cho một số nguyên tố để số ~a~ chuyển thành số ~b~.
Ví dụ, khoảng cách giữa ~100~ và ~360~ bằng ~4~ vì:
~100 \div 5 \times 2 \times 3 \times 3 = 360~
Yêu cầu: Tính khoảng cách giữa hai số ~a, b~ cho trước.
Input
- Gồm không quá ~10^5~ dòng, mỗi dòng chứa hai số nguyên dương ~a, b~ (~a, b \leq 10^6~), cách nhau bởi dấu cách, ứng với một bộ dữ liệu.
Output
- Với mỗi bộ dữ liệu, in ra trên một dòng một số nguyên duy nhất là khoảng cách giữa hai số ~a, b~ trong bộ dữ liệu đó.
Sample Test
Input
100 360
12 1
88 999
123456 123456
Output
4
3
8
0
Scoring
- Subtask 1 (~80\%~ số điểm): Số dòng không vượt quá ~10~
- Subtask 2 (~20\%~ số điểm): Không có ràng buộc gì thêm
Đếm số nguyên tố
Nộp bàiPoint: 1
Cho ~q~ truy vấn. Mỗi truy vấn gồm ~2~ số nguyên dương ~l~ và ~r~. Hãy đếm số lượng số nguyên tố từ ~l~ đến ~r~.
Input
- Dòng đầu tiên chứa số nguyên ~q~ (~q \leq 10^5~) - số lượng truy vấn.
- ~q~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~l~ và ~r~ (~1 \leq l \leq r \leq 10^6~).
Output
- In ra ~q~ dòng, dòng thứ ~i~ chứa kết quả của truy vấn ~i~.
Sample Test
Input:
5
4 20
2 10
1 18
1 100
1 1000
Output:
6
4
7
25
168
Cập nhật 1
Nộp bàiPoint: 1
Cho dãy ~a~ gồm ~n~ phần tử ~a_1, a_2, ..., a_n~. Thực hiện ~m~ thao tác, mỗi thao tác gồm ba số ~(l, r, x)~ có ý nghĩa: tăng các phần tử có chỉ số từ ~l~ đến ~r~ thêm ~x~ đơn vị.
Hãy in ra dãy ~a~ sau khi thực hiện ~m~ thao tác trên.
Input
- Dòng đầu tiên chứa hai số nguyên ~n, m \ (1 \le n, m\le 10^5)~.
- Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, ..., a_n \ (|a_i| \le 10^5, 1\le i\le n)~.
- ~m~ dòng sau, mỗi dòng chứa ba số nguyên ~l_i, r_i, x_i \ (1\le l_i \le r_i \le n, |x_i| \le 10^5, 1\le i\le m)~.
Output
Dãy ~a~ sau khi thực hiện hết ~m~ thao tác.
Ví dụ
Input
5 3
1 -2 3 -4 5
1 2 1
2 4 -2
1 5 3
Output
5 0 4 -3 8
Ma trận k
Nộp bàiPoint: 1
Cho ma trận kích thước ~n \times m~. Hãy tìm ma trận con vuông ~k \times k~ có tổng lớn nhất.
Input
- Dòng đầu chứa ~3~ số nguyên ~n, m~ và ~k~ (~2 \leq k \leq n,m \leq 1000~) - kích thước ma trận và ma trận con.
- ~n~ dòng tiếp theo, mỗi dòng chứa ~m~ số nguyên ~a_{i,j}~ phân cách bởi dấu cách (~0 \leq a_{i,j} \leq 1000~).
Output
- In ra tổng của ma trận con ~k \times k~ có tổng lớn nhất.
Sample Test
Input:
3 4 2
1 1 1 1
3 2 1 1
5 1 1 1
Output:
11
Đếm k
Nộp bàiPoint: 1
Cho ma trận kích thước ~n \times m~ và một số nguyên ~k~.
Cho ~q~ truy vấn, mỗi truy vấn gồm ~4~ số ~(x, y, u, v)~. Với mỗi truy vấn, hãy đếm số phần tử bằng ~k~ nằm trong bảng con có góc bên trái phía trên là ô ~(x, y)~ và góc bên phải phía dưới là ô ~(u, v)~.
Input
- Dòng đầu chứa ~3~ số nguyên ~n, m~ và ~k~ (~2 \leq n, m \leq 1000, 1 \leq k \leq 10^9~).
- ~n~ dòng tiếp theo, mỗi dòng chứa ~m~ số nguyên ~a_{i,j}~ phân cách bởi dấu cách (~0 \leq a_{i,j} \leq 1000~).
- Dòng thứ ~n+1~ chứa số nguyên ~q~ (~1 \leq q \leq 10^5~) - số lượng truy vấn.
- ~q~ dòng sau, mỗi dòng chứa bốn số nguyên ~x_i, y_i, u_i, v_i \ (1\le x_i \le u_i \le n, 1\le y_i \le v_i \le m, 1\le i\le q)~.
Output
- Kết quả gồm ~q~ dòng, dòng thứ ~i~ in ra kết quả của truy vấn ~i~.
Sample Test
Input:
3 4 2
1 5 3 2
3 2 1 5
1 4 3 3
2
1 1 2 2
2 3 3 4
Output:
1
0
Dãy ngoặc đúng 1
Nộp bàiPoint: 1
Điều kiện thoả mãn dãy ngoặc đúng được định nghĩa như sau:
- Dãy rỗng "" là một dãy ngoặc đúng.
- Nếu dãy ~A~ là một dãy ngoặc đúng thì ~(A)~ là một dãy ngoặc đúng.
- Nếu dãy ~A~ và dãy ~B~ là hai dãy ngoặc đúng thì ~A + B~ là một dãy ngoặc đúng.
Cho xâu ~s~ là một dãy ngoặc chỉ gồm 2 kí tự là ~(~ và ~)~, hãy kiểm tra xem xâu ~s~ có phải một dãy ngoặc đúng hay không.
Input
- Gồm một dòng chứa xâu ngoặc ~s~ ~(1 \le |s| \le 10^3)~.
Output
- In ra
Yesnếu xâu ~s~ là dãy ngoặc đúng, ngược lại in raNo.
Ví dụ
Input 1:
(()())
Output 1:
Yes
Input 2:
(()))
Output 2:
No
Đoạn số nguyên
Nộp bàiPoint: 1
Cho ~N~ đoạn số nguyên ~[a_i, b_i]~, hãy tìm số mà số đó thuộc nhiều đoạn số nguyên nhất?
Input
- Dòng đầu tiên chứa số nguyên ~N~ ~(N \leq 10^4)~ - số lượng đoạn.
- ~N~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~a_{i}, b_{i}~ có giá trị tuyệt đối không vượt quá ~10^{5}~.
Output
Ghi ra một hoặc nhiều số thuộc nhiều đoạn nhất theo thứ tự tăng dằn, trên một dòng, cách nhau bởi dấu cách.
Sample test
| Input | Output |
|---|---|
| 3 1 2 2 3 2 5 |
2 |
Tìm tổng lớn nhất
Nộp bàiPoint: 1
Thầy Tùng rất thích các bài toán về truy vấn mảng.
Một ngày nọ, thầy Tùng gặp phải một bài toán khá nổi tiếng: thầy được cho một mảng gồm ~n~ phần tử (các phần tử trong mảng được đánh chỉ số từ ~1~ đến ~n~), ngoài ra có ~q~ truy vấn, mỗi truy vấn có dạng ~(l, r)~: tính tổng các phần tử của mảng với chỉ số từ ~l~ đến ~r~.
Là một người thích sự mới mẻ, thầy quyết định sắp xếp lại các phần tử trong mảng trước khi trả lời các truy vấn sao cho tổng các kết quả truy vấn là lớn nhất có thể. Nhiệm vụ của bạn là tìm giá trị của tổng lớn nhất này.
Input
- Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ cách nhau bởi một khoảng trắng (~1 \leq n, q \leq 2 \times 10^5~) - số phần tử của mảng và số lượng truy vấn tương ứng.
- Dòng tiếp theo chứa ~n~ số nguyên ~a_1, a_2, \dots, a_n~ (~1 \leq a_i \leq 2 \times 10^5~) - các phần tử của mảng.
- Mỗi một trong ~q~ dòng tiếp theo chứa hai số nguyên ~l_i~ và ~r_i~ (~1 \leq l_i \leq r_i \leq n~) - truy vấn thứ ~i~.
Output
- In một số nguyên duy nhất trên một dòng - tổng lớn nhất của các câu trả lời truy vấn sau khi sắp xếp mảng.
Sample Test
Input:
3 3
5 3 2
1 2
2 3
1 3
Output:
25
Input:
5 3
5 2 4 1 3
1 5
2 3
2 3
Output:
33
Tính tổng 1
Nộp bàiPoint: 1
Cho dãy ~a~ gồm ~n~ phần tử ~a_1, a_2, ..., a_n~ và ~q~ truy vấn, mỗi truy vấn gồm hai số ~l, r~.
Với mỗi truy vấn, hãy tính tổng các phần tử có vị trí từ ~l~ đến ~r~.
Input
- Dòng đầu tiên chứa hai số nguyên ~n, q \ (1\le n, q\le 10^5)~.
- Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, ..., a_n \ (|a_i| \le 10^5, 1\le i\le n)~.
- ~q~ dòng sau, mỗi dòng chứa hai số nguyên ~l_i, r_i \ (1\le l_i \le r_i \le n, 1\le i\le q)~.
Output
Kết quả gồm ~q~ dòng, dòng thứ ~i~ là kết quả của truy vấn thứ ~i~ ~(1\le i\le q)~.
Ví dụ
Input
5 3
1 -2 3 -4 5
1 2
2 4
1 5
Output
-1
-3
3
Thay đổi dãy
Nộp bàiPoint: 1
Cho một dãy ~a~ gồm ~n~ số nguyên ~a_1, a_2, a_3, \ldots, a_n~. Bạn cần thực hiện ~Q~ truy vấn thuộc một trong ~2~ loại sau:
- Truy vấn loại ~1~: Tính tổng các số nguyên từ ~l~ đến ~r~ trong dãy ~a~ ban đầu.
- Truy vấn loại ~2~: Tính tổng các số nguyên từ ~l~ đến ~r~ trong dãy ~a~ đã sắp xếp không giảm.
Input
- Dòng đầu tiên chứa số nguyên dương ~n~ (~1 \leq n \leq 2 \times 10^5~).
- Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, a_3, \ldots, a_n~ (~|a_i| \leq 10^9~).
- Dòng thứ ba chứa số nguyên dương ~Q~ (~1 \leq Q \leq 10^5~) - số lượng truy vấn.
- ~Q~ dòng tiếp theo, mỗi dòng chứa ba số nguyên ~t, l, r~ biểu diễn truy vấn loại ~t~.
Output
- In ra ~Q~ dòng, mỗi dòng lần lượt chứa đáp án của mỗi truy vấn.
Sample Tests
| Input | Output |
|---|---|
| 6 6 4 2 7 2 7 3 2 3 6 1 3 4 1 1 6 |
24 9 28 |
|
4 5 5 2 3 10 1 2 4 2 1 4 1 1 1 2 1 4 2 1 2 1 1 1 1 3 3 1 1 3 1 4 4 1 2 2 |
10 15 5 15 5 5 2 12 3 5 |
BS6 - X xuất hiện bao nhiêu lần?
Nộp bàiPoint: 1
Cho ~1~ dãy số có ~N~ phần tử nguyên ~a_1, a_2, \dots, a_n~ đă được sắp xếp theo thứ tự không giảm.
Hãy trả lời ~T~ truy vấn:
- In ra số lần xuất hiện trong dãy của số ~X~ được nhập vào.
Input
- Dòng đầu tiên chứa số nguyên dương ~N~. (~N \leq 10^6~)
- Dòng thứ hai chứa ~N~ phần tử nguyên ~a_1, a_2, \dots, a_n~. (~|a_i| \leq 10^9~)
- Dòng thứ ba chứa số nguyên dương ~T~. (~T \leq 10^5~)
- Dòng thú tư chứa ~T~ số nguyên ~X~ tương ứng với ~T~ truy vấn. (~|X| \leq 10^9~)
Output
- In ra câu trả lời của các truy vấn trên một dòng, cách nhau bởi dấu cách.
Subtasks
- Subtask ~1~ (~50\%~ số điểm): ~N \leq 10^3~.
- Subtask ~2~ (~50\%~ số điểm): Không có thay đổi gì thêm.
Sample Test
Input:
8
1 1 1 3 3 3 5 5
5
1 3 5 0 6
Output:
3 3 2 0 0
Tập xe
Nộp bàiPoint: 1
Cô giáo trường tiểu học ~X~ đang dạy ~n~ học sinh tập xe đạp, được đánh số từ ~1~ tới ~n~, học sinh thứ ~i~ có trọng lượng là ~a_i~. Có một xe đạp duy nhất với tải trọng là ~m~, hai học sinh chỉ có thể cùng lên xe nếu tổng trọng lượng của hai học sinh không vượt quá ~m~.
Cô giáo tự hỏi có bao nhiêu cách chọn hai học sinh khác nhau cho cùng lên xe, sau nhiều giờ tính toán không có kết quả, cô quyết định hỏi bạn cách giải bài toán.
Yêu cầu: Đếm số cặp chỉ số ~i, j~ trong đó ~i < j~ và ~a_i + a_j \leq m~.
Input
- Dòng thứ nhất chứa hai số nguyên dương ~n, m~ (~m \leq 10^6~)
- Dòng tiếp theo chứa ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~ (~\forall{i}: a_i \leq 10^6~)
Output
- Ghi một số nguyên duy nhất là đáp số.
Subtasks
- Subtask 1 (~60\%~ số điểm): ~n \leq 10^4~.
- Subtask 2 (~20\%~ số điểm): ~n \leq 10^5~.
- Subtask 3 (~20\%~ số điểm): ~n \leq 10^6~.
Sample Test
Input:
5 6
1 2 3 4 5
Output:
6
Points in Segments
Nộp bàiPoint: 1
Cho ~n~ điểm (một chiều) và ~q~ đoạn, bạn cần tìm số lượng điểm nằm trong mỗi đoạn. Một điểm ~p_i~ sẽ nằm trong đoạn [~A, B~] nếu ~A \leq p_i \leq B~.
Ví dụ, nếu các điểm là ~1, 4, 6, 8, 10~ và đoạn là từ ~0~ đến ~5~, thì có ~2~ điểm nằm trong đoạn này.
Input
Gồm ~T~ bộ test (~T \leq 5~), mỗi bộ có cấu trúc như sau:
- Dòng đầu gồm hai số ~N~ và ~Q~ là số lượng điểm và số lượng truy vấn (~1 \leq N \leq 10^5; 1 \leq Q \leq 50000~).
- Dòng tiếp theo chứa ~N~ số nguyên dương phân biệt đã được sắp xếp theo thứ tự tăng dần có giá trị không quá ~10^8~.
- ~Q~ dòng sau, mỗi dòng chứa hai số nguyên dương ~l~, ~r~ (~0 \leq l \leq r \leq 10^8~) biểu diễn một đoạn thẳng.
Output
- Với mỗi truy vấn thứ ~i~, in ra ~Q~ dòng là số lượng điểm nằm trong mỗi đoạn tương ứng.
Sample Test
Input:
1
5 3
1 3 5 7 8
3 7
2 9
0 9
Output:
3
4
5
Bán cà phê dạo
Nộp bàiPoint: 1
Một buổi tối nọ, TDZ tổ chức một bữa tiệc ở quán cà phê của mình.
Có ~n~ người xuất hiện, người thứ ~i~ có chiều cao ~h_i~. Những bữa tiệc thì không thể thiếu đi những hoạt động vui vẻ nên TDZ quyết định ghép các cặp hai người cho một trò chơi team-building của mình. Vì không muốn để cho các cặp đôi trông quá chênh lệch về chiều cao, TDZ đã đưa ra yêu cầu:
Người thứ ~i~ và người thứ ~j~ (~i \neq j~) có thể ghép cặp được với nhau nếu ~90\% * h_j \leq h_i \leq h_j~. Hai các ghép cặp ~(i, j)~ và cặp ~(j, i)~ được coi là một.
Với số lượng người tham dự nhỏ TDZ có thể dễ dàng tính ra được số cách ghép các cặp khác nhau, nhưng do đã lỡ tay mời quá nhiều người nên việc tính toán của TDZ trở nên khó khăn hơn. Hãy giúp TDZ làm công việc này nhé.
Input
- Dòng đầu tiên chứa số nguyên dương ~n~ - Số người ở bữa tiệc (~1 \leq n \leq 10^5~).
- Dòng tiếp theo chứa ~n~ số nguyên dương ~h_1, h_2, h_3, \ldots, h_n~ tương ứng với chiều cao từng người (~h_i \leq 10^9~).
Output
In ra số cách chọn các cặp khác nhau.
Subtasks
- Subtask 1 (~50\%~): ~n \leq 10^3~.
- Subtask 2 (~50\%~): Không có điều kiện gì thêm.
Sample Test
Input:
6
100 89 90 101 91 99
Output:
11
Mua quà
Nộp bàiPoint: 1
Sau thành công từ quán cà phê nổi tiếng của mình, TDZ quyết định tự thưởng cho bản thân.
Ở cửa hàng có trưng bày ~n~ món hàng, món thứ ~i~ có giá ~v_i~. Với tổng số tiền ~x~ trong tay, TDZ muốn mua 2 món quà khác nhau có tổng giá trị lớn nhất và tất nhiên không vượt quá khả năng chi trả của mình. TDZ đang loay hoay không biết phải chọn món nào, bạn hãy giúp TDZ nhé.
Input
- Dòng đầu tiên chứa số nguyên dương ~n~ và ~x~ lần lượt là số món hàng và số tiền TDZ sở hữu (~2 \leq n \leq 10^5, x \leq 10^9~).
- Dòng tiếp theo chứa ~n~ số nguyên dương ~v_1, v_2, v_3, \ldots, v_n~ tương ứng với giá tiền từng món hàng (~v_i \leq 10^9~).
Output
In ra số tiền cần trả, hoặc 0 nếu TDZ không thể chọn được ~2~ món thoả mãn.
Subtasks
- Subtask 1 (~50\%~): ~n \leq 10^3~.
- Subtask 2 (~50\%~): Không có điều kiện gì thêm.
Sample Test
Input:
6 18
5 3 10 2 4 9
Output:
15
Note: Ở ví dụ trên TDZ sẽ chọn món thứ nhất và thứ ba. Tổng số tiền cần chi sẽ là ~5 + 10 = 15~.
Đoạn con
Nộp bàiPoint: 1
Cho dãy ~A~ gồm ~N~ phần tử số nguyên dương và một số nguyên dương ~K~.
Tìm mảng con liên tục có kích thước lớn nhất sao cho tất cả các mảng con liên tục có kích thước bé hơn hoặc bằng nó, đều có tổng các phần tử nhỏ hơn ~K~.
Input
- Dòng đầu là chứa số nguyên ~N~ (~N \leq 10^6~) và số nguyên ~K~ (~K \leq 10^{12}~)
- Dòng tiếp theo ghi ~N~ số nguyên thuộc dãy, các số cách nhau bởi dấu cách.
Output
- Ghi kích thước mảng con lớn nhất cần tìm, nếu không tìm được mảng con nào thì in ra
-1.
Sample Test
Input:
4 8
1 2 3 4
Output:
2
Input:
4 8
1 2 10 4
Output:
-1
Note
Trong ví dụ 1, tổng dãy con có:
- Độ dài ~1~: 1,2,3,4
- Độ dài ~2~: 3,5,7
- Độ dài ~3~: 6,9
- Độ dài ~4~: 10
Tổng đoạn con không âm
Nộp bàiPoint: 1
Cho một dãy gồm ~n~ số nguyên ~a_1, a_2, a_3, \ldots, a_n~. Tìm đoạn con liên tiếp dài nhất có tổng không âm.
Input
- Dòng đầu tiên chứa số nguyên dương ~n~ (~n \leq 10^5~).
- Dòng tiếp theo chứa ~n~ số nguyên ~a_1, a_2, a_3, \ldots, a_n~ (~|a_i| \leq 10^9)~.
Output
In ra độ dài đoạn con thoả mãn. Nếu không tồn tại đoạn con thoả mãn in ra -1.
Subtasks
- Subtask ~1~ (~50\%~): ~n \leq 10^3~.
- Subtask ~2~ (~50\%~): Không có điều kiện gì thêm.
Sample Test
Input:
5
-1 -1 2 -2 -3
Output:
3
Dino ăn chuối
Nộp bàiPoint: 1
Dino rất thích ăn chuối. Có ~N~ nải chuối trước mặt Dino, nải thứ ~i~ chứa ~A_i~ quả.
Mẹ của Dino muốn bạn ấy ăn chuối lành mạnh. Bà ấy sẽ tới văn phòng và sẽ quay trở lại trong ~H~ giờ. Dino muốn đảm bảo rằng có thể ăn hết đống chuối vào lúc đó. Giả sử Dino đang ăn với tốc độ ~K~ quả chuối mỗi giờ. Ở mỗi giờ, bạn ấy sẽ chọn một số nải không rỗng và ăn ~K~ quả chuối từ đó (nếu nó có ít nhất ~K~ quả, nếu không Dino sẽ ăn tất cả đống ấy và kết thúc tiếng đó).
Dino thích ăn từ từ, nhưng vẫn muốn ăn hết đống chuối ấy. Tức là Dino thích tối thiểu ~K~ sao cho bạn ấy có thể ăn hết chuối trong ~H~ giờ. Giúp Dino tìm giá trị của ~K~.
Input
- Dòng đầu tiên chứa ~T~ (~1 \leq T \leq 10~) – biểu thị số test.
- Dòng đầu tiên của mỗi test chứa hai số nguyên ~N~ và ~H~ (~1 \leq N \leq 10^5, N \leq H \leq 10^9~) - số nải chuối và số giờ mẹ đi vắng.
- Dòng tiếp theo chứa ~N~ số nguyên, số thứ ~i~ thể hiện ~A_i~ (~A_i \leq 10^9~).
Output
Ở mỗi test, in ra một số thể hiện số thao tác ít nhất cần thực hiện.
Sample Test
Input:
3
3 3
1 2 3
3 4
1 2 3
4 5
4 3 2 7
Output:
3
2
4
Books
Nộp bàiPoint: 1
Khi Tôm có thời gian rảnh, cậu ta thường đến thư viện để đọc sách. Hôm nay, Tôm có ~t~ (phút) rảnh rỗi để đọc sách. Vì vậy, cậu ta đã mượn ~n~ cuốn sách từ thư viện và ước lượng thời gian cần để đọc mỗi cuốn sách. Gọi các cuốn sách được đánh số từ ~1~ đến ~n~, Tôm cần ~a_i~ phút để đọc cuốn sách thứ ~i~.
Tôm quyết định chọn một cuốn sách bất kỳ có số thứ tự ~i~ và bắt đầu đọc sách lần lượt từ cuốn này. Nói cách khác, anh sẽ đọc cuốn sách thứ ~i~, sau đó là cuốn thứ ~i+1~, rồi cuốn thứ ~i+2~, và tiếp tục như vậy. Quá trình này sẽ dừng lại khi Tôm hoặc hết thời gian rảnh hoặc đọc xong cuốn sách thứ ~n~. Tôm đọc từng cuốn sách đến hết, nghĩa là anh sẽ không bắt đầu đọc một cuốn sách nếu không đủ thời gian để đọc xong cuốn đó.
Hãy in ra số lượng sách tối đa mà Tôm có thể đọc.
Input
- Dòng đầu tiên chứa hai số nguyên ~n~ và ~t~ (~1 \leq n \leq 10^5; 1 \leq t \leq 10^9~) - số lượng sách và số phút rảnh rỗi của Tôm.
- Dòng thứ hai chứa dãy ~n~ số nguyên ~a_1, a_2, \dots, a_n~ (~1 \leq a_i \leq 10^4~) - trong đó ~a_i~ là số phút cần để đọc cuốn sách thứ ~i~.
Output
- In ra một số nguyên duy nhất - số lượng sách tối đa mà Tôm có thể đọc.
Sample Test
| Input | Output |
|---|---|
| 4 5 3 1 2 1 |
3 |
| 3 3 2 2 3 |
1 |
BINPOW
Nộp bàiPoint: 1
Hãy tính toán các giá trị ~a^b \mod 10^9~ ~+ 7~ một cách hiệu quả.
Lưu ý: Trong bài này, ta giả định rằng ~0^0 = 1~.
Input
- Dòng đầu tiên chứa một số nguyên ~n:~ số lượng câu hỏi.
- Sau đó là ~n~ dòng, mỗi dòng chứa hai số ~a,b~.
Output
- In ra các giá trị ~a^b \mod 10^9~ ~+~ ~7~.
Constraints
- ~1 \leq n \leq 2 \cdot 10^5~
- ~0 \leq a, b \leq 10^9~
Example
Sample input
3
3 4
2 8
123 123
Sample output
81
256
921450052
TPrime
Nộp bàiPoint: 1
Chúng ta đã quá rõ việc một số nguyên tố (prime) là số nguyên dương lớn hơn ~1~ có duy nhất hai ước là ~1~ và chính nó. Để làm mới bài toán, hôm nay, ta sẽ định nghĩa một số TPrime là một số nguyên dương lớn hơn ~1~ gồm đúng ~3~ ước.
Cho ~n~ truy vấn, mỗi truy vấn là một số ~a~, hãy kiểm tra xem số này có phải là số TPrime hay không.
Input
- Dòng ~1~ ghi số nguyên dương ~n~ ~(1 \le n \le 3*10^5)~
- ~n~ dòng sau, mỗi dòng gồm một số nguyên dương ~a~ ~(1 \le a \le 10^{12})~ miêu tả truy vấn.
Output
- In ra ~n~ dòng, với mỗi truy vấn, nếu ~a~ là số TPrime thì in ra "YES", ngược lại in ra "NO".
Subtask
- Có ~20\%~ số test ứng với ~1 \le n \le 100, 1 \le a \le 10^4~
- Có ~30\%~ số test ứng với ~1 \le n,a \le 10^5~
- Có ~50\%~ số test còn lại không có giới hạn gì thêm.
Sample Input 1
3
4
6
7
Sample Output 1
YES
NO
NO
Xoá số
Nộp bàiPoint: 1
Cho số nguyên dương ~N~. Hãy đếm số cách xoá đi một đoạn chữ số liên tiếp của ~N~ (không được xoá hết) để nhận được số mới chia hết cho ~3~, biết rằng số mới nhận được có thể có thừa chữ số ~0~ ở đầu.
Hai cách xoá được coi là khác nhau nếu có một vị trí được xoá trong cách này nhưng không được xoá trong cách kia.
Input
- Gồm một dòng duy nhất chứa một số nguyên ~N~ (~1 \le N \le 10^{100000}~).
Output
- In ra một số nguyên là số cách xoá tìm được.
Subtasks
- Subtask 1 (~50\%~ số điểm): ~N \le 10^{300}~.
- Subtask 2 (~25\%~ số điểm): ~N \le 10^{10000}~.
- Subtask 3 (~25\%~ số điểm): Không có ràng buộc gì thêm.
Sample Test 1
Input
1005
Output
4
Sample Test 2
Input
2009
Output
3
qsum
Nộp bàiPoint: 1
Cho dãy ~a~ nguyên dương gồm ~n~ phần tử. Ta định nghĩa hàm ~f(l,r)~ như sau: ~f(l,r) = 1\times a[l] + 2\times a[l+1] + 3\times a[l+2] + ... (r-l+1)\times a[r]~.
Có ~q~ truy vấn, mỗi truy vấn gồm hai số ~l~, ~r~ với ~1 \le l \le r \le n~. Với mỗi truy vấn, hãy in ra ~f(l,r)~.
Input
- Dòng đầu gồm 2 số nguyên dương ~n~ và ~q~. ~(1 \le n, q \le 10^5)~
- Dòng thứ hai gồm ~n~ số nguyên dương miêu tả dãy ~a~. ~(1 \le a[i] \le 10^5)~.
- ~q~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên dương ~l~, ~r~ miêu tả các truy vấn.
Ouput
- In ra ~q~ dòng, mỗi dòng là kết quả của một truy vấn tương ứng.
Subtask
- Subtask ~1~: ~n,q \le 2 \times 10^3~ ~(30\%)~
- Subtask ~2~: Trong tất cả các truy vấn, ~l=1~.
- Subtask ~3~: Không giới hạn gì thêm ~(40\%)~.
Sample Test
Input
4 3
1
2
3
4
1 2
2 3
1 4
Output
5
8
30
Chẵn lẻ
Nộp bàiPoint: 1
Cho một mảng gồm ~n~ số nguyên dương ~a_1, a_2, ..., a_n~. Gọi trọng số của mảng là tổng của các cặp phần tử có tổng là lẻ. Nói cách khác, tìm tổng của các cặp số ~(i, j)~ thỏa mãn ~a_i + a_j~ lẻ ~(1 \le i \le j \le n)~. Hãy tìm trọng số của mảng ~a~.
Input
- Dòng đầu tiên gồm số nguyên dương ~n~.
- Dòng thứ hai gồm ~n~ số nguyên dương ~a_1, a_2, ..., a_n~.
Constraints
- ~1 \le n \le 10^5~.
- ~1 \le a_i \le 10^5~.
Subtask
- Subtask ~1~ ~(40\%)~: ~1 \le n \le 10^3~.
- Subtask ~2~ ~(60\%)~: Không có điều kiện gì thêm.
Output
- Gồm một số duy nhất là đáp án bài toán.
Sample Input 1:
5
3 7 2 1 9
Sample Output 1:
28
Explanation 1:
Các cặp thỏa mãn là ~(1, 3)~, ~(2, 3)~, ~(3, 4)~, ~(3, 5)~. Tổng sẽ là ~a_1 + a_3 + a_2 + a_3 + a_3 + a_4 + a_3 + a_5~ = ~3 + 2 + 7 + 2 + 2 + 1 + 2 + 9 = 28~.
PNumber
Nộp bàiPoint: 1
Bé Tommy rất thích tìm hiểu về các số đặc biệt, hôm trước trong giờ học lập trình thầy giáo dạy cho bé về số hoàn hảo (số hoàn hảo là số có tổng các ước (không kể nó) bằng chính nó, ví dụ số ~6~ là số hoàn hảo vì ~6=1+2+3~), bé cảm thấy hứng thú với con số này. Về nhà bé nghĩ ra khá nhiều bài toán xử lí số hoàn hảo. Nhưng hôm nay, thầy cho bé một bài tập rất hóc búa, nghĩ mãi không ra cách làm tốt nhất để được tối đa điểm của bài, nên bé nhờ các bạn học sinh giỏi làm giúp. Bài toán như sau:
Cho dãy ~a_1,a_2,…,a_n~ , ban đầu tất cả các phần tử có giá trị bằng ~0~. Có ~m~ phép biến đổi dạng ~(u,v,k)~: tăng giá trị các phần tử từ vị trí ~u~ đến vị trí ~v~ lên ~k~ đơn vị. Dữ liệu đảm bảo sau ~m~ phép biến đổi ~0<a_i \le 10^6~ ~(\forall i=1..n)~ và có ít nhất một số hoàn hảo trong dãy. </p>
Yêu cầu:
- Với dãy ~a_1,a_2,…,a_n~ sau ~m~ phép biến đổi, thầy yêu cầu đưa ra vị trí các số hoàn hảo theo thứ tự tăng dần.
Input
- Dòng đầu là hai số nguyên dương ~n,m~ tương ứng là số phần tử của dãy và số lượng phép biến đổi;
- ~m~ dòng sau mỗi dòng là ba số nguyên dương ~u,v,k~ ~(0 < u \le v \le n)~.
Output
- In ra các dòng, mỗi dòng chứa một số nguyên dương là vị trí của số hoàn hảo tìm được trong dãy theo thứ tự tăng dần.
Subtask
- Subtask ~1~ (~35\%~ số điểm): ~ 1 \le n,m \le 10^2~
- Subtask ~2~ (~35\%~ số điểm): ~n \le 10^5, m \le 10^3~
- Subtask ~3~ (~30\%~ số điểm): ~n \le 10^5, m \le 10^5~
Sample Input 1
6 3
1 6 6
2 3 4
3 5 22
Sample Output
1
4
5
6
Explanation 1
- Dãy thu được sau ~3~ phép biến đổi là:
6 10 32 28 28 6
Turtle Graph
Nộp bàiPoint: 1
Mrtee đang lặn lội trên con đường tìm ma pháp sư Marisa thì có một con Rùa và một con Thỏ cãi nhau xem ai nhanh hơn. Chúng quyết định giải quyết việc tranh luận bằng một cuộc thi chạy đua. Chúng đồng ý lộ trình và bắt đầu cuộc đua.
Thỏ xuất phát nhanh như tên bắn và chạy thục mạng rất nhanh, khi thấy rằng mình đã khá xa Rùa, Thỏ nghĩ nên nghỉ cho đỡ mệt dưới một bóng cây xum xê lá bên vệ đường và nghỉ thư giãn trước khi tiếp tục cuộc đua.
Vì quá tự tin vào khả năng của mình, Thỏ ngồi dưới bóng cây và nhanh chóng ngủ thiếp đi trên đường đua. Rùa từ từ vượt qua Thỏ và sớm kết thúc đường đua.
Khi Thỏ thức dậy thì rùa đã đến đích và trở thành người chiến thắng. Thỏ giật mình tỉnh giấc và nhận ra rằng nó đã bị thua.
Không thể chấp nhận sự thật, Thỏ quyết định tái đấu. Lần này, thay vì dùng một trò thiên về sức lực, Thỏ quyết định thách đấu bằng cách đố Rùa một câu hỏi đầy hóc búa.
Cho đồ thị vô hướng gồm ~n~ đỉnh và ~m~ cạnh, không có khuyên và cạnh lặp.
Để tạo ra được một đồ thị có độ đẹp, ta cần điền các số nguyên dương ~c~ trên mỗi đỉnh (~c~ chỉ có thể là ~1~, ~2~, hoặc ~3~), sao cho với mỗi cạnh, tổng của hai số được điền trên ~2~ đỉnh được kết nối bởi cạnh đó là một số lẻ.
Thỏ đố Rùa có thể đếm số cách để điền các số ~1,2,3~ lên mỗi đỉnh sao cho tạo ra được một đồ thị đẹp. Do con số này có thể rất lớn, hãy in nó ra theo ~modulo~ ~998244353~.
Lưu ý: Rùa phải điền đúng một số trên mỗi đỉnh.
Để cho câu đố thêm phần học búa, Thỏ sẽ hỏi ~q~ câu có dạng như vậy.
Rùa dù là một sinh vật cute nhưng không giỏi đồ thị cho lắm, hãy giúp Rùa hoàn thành bài toán này nhé!
Input
- Dòng đầu tiên gồm số nguyên dương ~q~ miêu tả số câu hỏi.
- Đối với mỗi câu hỏi:
- Dòng đầu tiên ~2~ số nguyên dương ~n,m~ miêu tả số đỉnh và cạnh của đồ thị.
- ~m~ dòng tiếp theo, mỗi dòng gồm ~2~ số nguyên dương ~u_i,v_i~ ~(1 \le u_i,v_i \le n, u_i \neq v_i)~ miêu tả cạnh thứ ~i~.
Output
- Với mỗi câu hỏi, in ra một dòng là số nguyên duy nhất là số cách điền thỏa mãn sau khi lấy phần dư cho ~998244353~.
Điều kiện
- ~1 \le q \le 3 \times 10^5~.
- ~1 \le n,m \le 3 \times 10^5~.
- Dữ liệu đảo bảo rằng tổng ~n~ trong tất cả các câu hỏi không vượt quá ~3 \times 10^5~, tương tự với tổng ~m~.
Subtask
- ~50\%~ số điểm: ~n \le 10, q \le 10~.
- ~30\%~ số điểm: Trong mọi câu hỏi, đồ thị có dạng cây.
- ~20\%~ số điểm: Không có ràng buộc gì thêm.
Ví dụ
Input:
2
7 7
1 2
2 3
3 4
4 5
5 6
6 7
7 1
2 1
2 1
Output:
0
4
Giải thích:
Ở câu hỏi đầu tiên, không có cách điền nào thỏa mãn.
Ở câu hỏi thứ hai, có ~4~ cách điền như sau:
- Điền số ~1~ vào đỉnh ~1~, số ~2~ vào đỉnh ~2~.
- Điền số ~3~ vào đỉnh ~1~, số ~2~ vào đỉnh ~2~.
- Điền số ~2~ vào đỉnh ~1~, số ~1~ vào đỉnh ~2~.
- Điền số ~2~ vào đỉnh ~1~, số ~3~ vào đỉnh ~2~.
Nhà máy điện
Nộp bàiPoint: 1
Ở một vương quốc nọ có ~n~ thành phố, được đánh số từ ~1~ đến ~n~. Mạng lưới giao thông của vương quốc gồm ~m~ con đường, con đường thứ ~i~ nối hai thành phố ~u_i~ và ~v_i~ với độ dài đúng bằng ~1~ ki-lô-mét.
Có ~k~ dự án nhà máy điện đang được triển khai, dự án thứ ~j~ sẽ xây một nhà máy điện đặt tại thành phố ~p_j~, cung cấp điện cho tất cả các thành phố nằm trong bán kính ~r_j~ ki-lô-mét (giả sử rằng quãng đường di chuyển trong nội thành là bằng ~0~). Nhà vua đang băn khoăn, những thành phố nào đã được cấp điện, và những thành phố nào chưa được cấp điện? Hãy giúp nhà vua giải quyết bài toán này nhé.
Input
Dòng đầu chứa ba số nguyên ~n~, ~m~, ~k~ (~2 \le n, m \le 2 \times 10^5~; ~0 \le k \le 5 \times 10^5~).
~m~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~u_i~, ~v_i~ (~1 \le u_i, v_i \le n~; ~u_i \ne v_i~) mô tả con đường thứ ~i~.
~k~ dòng tiếp theo, dòng thứ ~j~ chứa hai số nguyên ~p_j~, ~r_j~ (~1 \le p_j \le n~; ~0 \le r_j \le 10^9~) mô tả dự án thứ ~j~.
Output
Gồm một dòng duy nhất chứa một xâu nhị phân gồm ~n~ kí tự, kí tự thứ ~i~ bằng "1" nếu thành phố thứ ~i~ đã được cấp điện, ngược lại kí tự thứ ~i~ bằng "0" nếu thành phố thứ ~i~ chưa được cấp điện.
Scoring
- Subtask ~1~ (~40\%~ số điểm): ~n, m \le 1000~.
- Subtask ~2~ (~30\%~ số điểm): ~r_1 = r_2 = \dots = r_{k - 1} = r_k~.
- Subtask ~3~ (~30\%~ số điểm): Không có ràng buộc gì thêm.
Example
Input 1
4 3 1
1 2
1 3
2 4
2 1
Output 1
1101
Input 2
6 8 2
1 3
1 5
1 6
2 5
2 6
3 4
3 5
5 6
6 0
3 1
Output 2
101111
IncLad
Nộp bàiPoint: 1
Cho một dãy ~a~ gồm ~n~ phần tử nguyên không âm.
Có ~q~ truy vấn, mỗi truy vấn có dạng ~l,r,d~, có nghĩa là tăng phần tử thứ ~l~ lên ~d~ đơn vị, phần tử thứ ~l+1~ lên ~2*d~ đơn vị, ..., phần tử thứ ~r~ lên ~(r-l+1)*d~ đơn vị. Nói cách khác, phần tử thứ ~i \in [l,r]~ sẽ được tăng thêm ~(i-l+1)*d~ đơn vị.
Hãy in ra dãy ~a~ sau khi thực hiện đủ ~q~ truy vấn.
Input
- Dòng đầu tiên chứa số nguyên dương ~n~
- Dòng thứ hai gồm ~n~ số nguyên không âm miêu tả dãy ~a~.
- ~q~ dòng sau, mỗi dòng gồm ~3~ số nguyên ~(l,r,d)~ miêu tả truy vấn.
Output
- Gồm một dòng in ra ~n~ số, số thứ ~i~ là giá trị của phần tử ~a_i~ sau khi thực hiện ~q~ truy vấn.
Điều kiện
- ~1 \le n,q \le 10^6~.
- ~0 \le a_i,d_i \le 10^5~.
Subtask
- ~50\%~ số điểm: ~n \le 1000~.
- ~50\%~ số điểm: ~n \le 10^5~.
Ví dụ
Input 1:
1
10
3
1 1 40
1 1 0
1 1 -15
Output 1:
35
Input 2:
5
1 2 3 4 -5
3
5 5 10
1 5 4
2 3 -1
Output 2:
5 9 13 20 25
Light
Nộp bàiPoint: 1
Đường Hà Nội có ~n~ cái cột đèn được đánh số từ ~1~ đến ~n~. Tuy nhiên, trận bão tàn khốc vừa qua đã khiến ~t~ ~(t \leq n)~ cây đèn này bị đổ.
Sắp tới thầy Tùng cần tổ chức một lễ hội ẩm thực tại đây, và yêu cầu cần tổ chức tại nơi có ít nhất ~k~ cái đèn còn nguyên vẹn liên tiếp. Vì thời gian gấp rút, bạn được thầy yêu cầu tìm xem cần phải sửa chữa ít nhất bao nhiêu cây đèn để có thể tổ chức lễ hội.
Input
- Dòng đầu tiên gồm ba số nguyên dương ~n, k, t~ ~(1 \le t, k \le n \le 10^5)~.
- ~t~ dòng tiếp theo, mỗi dòng gồm một số nguyên dương là vị trí có cây đèn bị đổ.
Output
- In ra một số nguyên duy nhất là số cây đèn cần được sửa chữa.
Sample Test
Input:
10 6 5
2
10
1
5
9
Output:
1
Note:
Sửa cây đèn tại vị trí ~5~ và chọn các cây ~3, 4, 5, 6, 7, 8~ để tổ chức lễ hội.
MaxMod
Nộp bàiPoint: 1
Cho dãy số gồm ~n~ số nguyên ~c_1, c_2, …, c_n~ và số nguyên dương ~m~. Nhiệm vụ của bạn là tìm một đoạn ~b_1,b_2,...,b_k~ ~(1 \le b_1 < b_2 < ... < b_k \le n)~ sao cho ~(\sum c_{b_i}) \% m~ là lớn nhất có thể. Đoạn con tìm được có thể rỗng.
Yêu cầu: Hãy in ra giá trị lớn nhất tìm được.
Input
- Dòng đầu tiên chứa ~2~ số nguyên duyên ~n,m~
- Dòng thứ hai chứa dãy ~c~ gồm ~n~ phần tử.
Output
- Một số nguyên duy nhất là giá trị lớn nhất tìm được.
Constraints
- ~1 \le n \le 40~
- ~1 \le m \le 10^9~
- ~1 \le c_i \le 10^9~
Subtask
- Có ~50\%~ số test ứng với ~n \le 20~.
- Có ~50\%~ số test ứng với ~n \le 40~.
Sample Input 1
4 4
5 2 4 1
Sample Output 1
3
Sample Input 2
3 20
199 41 299
Sample Output 2
19