Một dãy số gồm ~M~ phần tử ~a_1, a_2, ..., a_M~ được gọi là dãy số hai phía nếu thoả mãn điều kiện sau:

• ~M~ chẵn, khi đó chia dãy thành hai phần ~\{a_1, a_2, ..., a_{\frac{M}{2}}\}~ và ~\{a_{\frac{M}{2}+1}, ..., a_M\}~;
• Các phần tử ở mỗi phần có giá trị bằng nhau. Tức là ~a_1=a_2=...=a_{\frac{M}{2}}~ và ~a_{\frac{M}{2}+1}=...=a_M~;
• Giá trị của hai phần phải khác nhau. Tức là ~a_1 \neq a_M~.

Ví dụ:

• Dãy số hai phía: ~\{0, 0, 0, 1, 1, 1\}, \{1, 1, 2, 2\}, \dots~
• Không phải dãy hai phía: ~\{1, 1, 0\}, \{0, 0, 2, 1\}, \{2, 2\}, \dots~

Cho dãy số gồm ~N~ phần tử, mỗi phần tử nhận một trong ba giá trị ~0, 1, 2~ và số nguyên dương ~K~.

Hãy thay đổi không quá ~K~ phần tử của dãy để được dãy con dài nhất là dãy số hai phía.

Dữ liệu vào từ tệp văn bản DSHP.INP:

• Dòng đầu tiên chứa hai số nguyên ~N, K~ ~(1\le K\le N\le 10^5)~;
• Dòng tiếp theo chứa ~N~ số ~0~ hoặc ~1~ hoặc ~2~ mô tả dãy số ban đầu.

Kết quả ghi ra tệp văn bản DSHP.OUT:

Một số nguyên duy nhất là độ dài lớn nhất của dãy số hai phía tìm được, sau khi thay đổi không quá ~K~ số của dãy số đã cho.

Ví dụ

Input

7 3
2 1 2 0 0 2 1

Output

6

Giải thích

Có thể thay đổi thành dãy số: ~\color{red}{2, \underline{2}, 2, 0, 0, \underline{0}}~~, 1~

Hoặc cũng có thể thay đổi thành dãy số: ~\color{red}{\underline{1}, 1, \underline{1}, 0, 0, \underline{0}}~~, 1~

---

Input

4 2
1 1 0 0

Output

4

Giải thích

Không cần thay đổi phần tử nào trong dãy số.

Ràng buộc

• Có ~50\%~ số test ứng với ~50\%~ số điểm thoả mãn: ~1\le K\le N\le 10^2~;
• ~30\%~ số test khác ứng với ~30\%~ số điểm thoả mãn: ~1\le K\le N\le 10^3~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho xâu ~S~ gồm các chữ cái tiếng Anh in thường. Gọi ~f(S)~ là số lượng kí tự phân biệt của xâu ~S~. Ví dụ ~S =~ abccaaa, vậy ~f(S)=3~.

Với mỗi ~K~ có giá trị từ ~1~ đến ~f(S)~, hãy đếm số lượng xâu con ~X~ của ~S~ có ~f(X) = K~.

Dữ liệu vào từ tệp văn bản KTPB.INP:

Gồm một xâu ~S~ (có số lượng kí tự - kí hiệu là ~|S|~ không vượt quá ~10^6~).

Kết quả ghi ra tệp văn bản KTPB.OUT:

Gồm ~f(S)~ dòng, mỗi dòng là kết quả tương ứng khi ~K~ có giá trị từ ~1~ đến ~f(S)~.

Ví dụ

Input

abba

Output

5
5

Giải thích

Các xâu con có ~1~ kí tự phân biệt là (xâu được gạch chân): ~\underline{a} \textit{bba}, \textit{a}\underline{b}\textit{ba}, \textit{ab}\underline{b}\textit{a}, \textit{abb}\underline{a}, \textit{a}\underline{bb}\textit{a}~

Các xâu con có ~2~ kí tự phân biệt là (xâu được gạch chân): ~\underline{ab}\textit{ba}, \underline{abb}\textit{a}, \underline{abba}, \textit{a}\underline{bba}, \textit{ab}\underline{ba}~

Ràng buộc

• Có ~40\%~ số test ứng với ~40\%~ số điểm thoả mãn: ~|S|\le 10^2~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~|S|\le 2\times 10^3~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~|S|\le 10^5~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho dãy số gồm ~N~ số nguyên dương ~a_1, a_2, \dots, a_N~. Thao tác gộp dãy số lại như sau: chọn hai phần tử liên tiếp ~a_i~ và ~a_{i+1}~ có cùng giá trị là ~x~, rồi xoá ~a_{i+1}~ khỏi dãy và tăng ~a_i~ lên ~1~ thành ~x+1~, sau đó các phần tử còn lại của dãy được gộp lại.

Hãy tìm cách thực hiện liên tục các thao tác như trên để được dãy có ít phần tử nhất.

Dữ liệu vào từ tệp văn bản GDS.INP:

• Dòng đầu tiên chứa số nguyên dương ~N \ (1\le N\le 10^6)~;
• Dòng thứ hai chứa ~N~ số nguyên ~a_i~ ~(1\le a_i\le 10^9; \ 1\le i\le N)~.

Kết quả ghi ra tệp văn bản GDS.OUT:

Ghi ra số lượng phần tử ít nhất có thể của dãy sau khi thực hiện liên tục các thao tác như trên để được dãy có ít phần tử nhất.

Ví dụ

Input

4
3 2 2 2

Output

2

Giải thích

Các bước gộp dãy số như sau:

• Dãy ban đầu: ~3 \ \underline{2} \ \underline{2} \ 2~
• Gộp hai số ở vị trí ~2~ và ~3~ thì dãy số là: ~\underline{3} \ \underline{3} \ 2~
• Gộp hai số ở vị trí ~1~ và ~2~ thì dãy số là: ~4 \ 2~

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm thoả mãn: ~N\le 10; \ a_i\le 30~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N\le 200; \ a_i\le 30~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N\le 2000; \ a_i\le 30~;
• ~10\%~ số test khác ứng với ~10\%~ số điểm thoả mãn: ~N\le 2000~;
• ~10\%~ số test khác ứng với ~10\%~ số điểm thoả mãn: ~a_i\le 30~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho một cây gồm ~N~ đỉnh được đánh số từ ~1~ đến ~N~, trong đó đỉnh ~1~ là gốc của cây. Tất cả đỉnh trên đường đi từ đỉnh ~1~ đến đỉnh ~u~ được gọi là tổ tiên của đỉnh ~u~. Mỗi đỉnh đều có hai loại trọng số, đỉnh thứ ~i~ có trọng số đỉnh là ~a_i~ và trọng số tổ tiên là ~b_i~.

Tổ tiên chung gần nhất của một tập đỉnh là đỉnh chung đầu tiên của các đỉnh khi đi về đỉnh gốc ~1~ (nếu tập hợp gồm ~1~ đỉnh thì tổ tiên chung gần nhất là chính đỉnh đó). Ví dụ, như hình dưới, tổ tiên chung gần nhất của tập hợp đỉnh ~\{3, 7\}~ là đỉnh ~2~; tổ tiên chung gần nhất của tập hợp đỉnh ~\{4, 7, 1\}~ là đỉnh ~1~.

Xét một tập hợp gồm ~k \ (0 \lt k \le N)~ đỉnh phân biệt bất kì ~\{u_1, u_2, \dots, u_k\}~. Gọi ~p~ là tổ tiên chung gần nhất của ~k~ đỉnh. Khi đó giá trị của tập đỉnh này được tính bằng công thức: ~a_{u_1} \times a_{u_2} \times \dots \times a_{u_k} \times b_p~. Vậy một cây ~N~ đỉnh sẽ có ~2^N - 1~ tập đỉnh phân biệt.

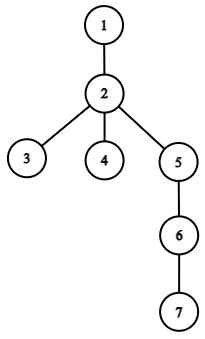
Hãy tính tổng giá trị của tất cả các tập đỉnh có thể tạo ra.

Dữ liệu vào từ tệp văn bản TSTD.INP:

• Dòng đầu tiên chứa số nguyên dương ~N \ (N \le 10^6)~ là số đỉnh của cây;
• Dòng thứ hai chứa ~N~ số nguyên dương ~a_1, a_2, \dots, a_N \ (a_i \le 10^9; \ 1\le i\le N)~ mô tả trọng số đỉnh của các đỉnh tương ứng từ đỉnh ~1~ đến đỉnh ~N~;
• Dòng thứ ba chứa ~N~ số nguyên dương ~b_1, b_2, \dots, b_N \ (b_i \le 10^9; \ 1\le i\le N)~ mô tả trọng số khi nó là tổ tiên của các đỉnh tương ứng từ đỉnh ~1~ đến đỉnh ~N~;
• ~N - 1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương ~u, v \ (u, v\le N)~ mô tả cạnh của cây.

Kết quả ghi ra tệp văn bản TSTD.OUT:

Gồm một số nguyên duy nhất là kết quả của bài toán, vì kết quả có thể rất lớn nên in ra phần dư của kết quả khi chia cho ~10^9+7~.

Ví dụ

Input

3
1 1 2
2 1 2
1 2
1 3

Output

21

Giải thích

• Tập đỉnh ~\{1\}~ có giá trị: ~2~
• Tập đỉnh ~\{2\}~ có giá trị: ~1~
• Tập đỉnh ~\{3\}~ có giá trị: ~4~
• Tập đỉnh ~\{1, 2\}~ có giá trị: ~2~
• Tập đỉnh ~\{1, 3\}~ có giá trị: ~4~
• Tập đỉnh ~\{2, 3\}~ có giá trị: ~4~
• Tập đỉnh ~\{1, 2, 3\}~ có giá trị: ~4~

~\Rightarrow~ Tổng là: ~21~

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm có ~N \le 15~ và cây có dạng đường thẳng: đỉnh ~1~ nối với đỉnh ~2~, đỉnh ~2~ nối với đỉnh ~3~, ..., đỉnh ~N-1~ nối với đỉnh ~N~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm có ~N\le 15~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm có cây có dạng đường thẳng: đỉnh ~1~ nối với đỉnh ~2~, đỉnh ~2~ nối với đỉnh ~3~, ..., đỉnh ~N-1~ nối với đỉnh ~N~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm có mọi trọng số đỉnh của các đỉnh đều là ~1~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho dãy số gồm ~N~ số nguyên dương ~a_1, a_2, \dots, a_N~. Có ~Q~ truy vấn, mỗi truy vấn cho hai số nguyên ~l~ và ~r~ có ý nghĩa: đếm số cặp chỉ số ~(i, j)~ sao cho ~l\le i, j\le r~ và ~a_i~ chia hết cho ~a_j~ (hai cặp chỉ số ~(i, j)~ và ~(j, i)~ là khác nhau).

Dữ liệu vào từ tệp văn bản CSCH.INP:

• Dòng đầu tiên gồm hai số nguyên dương ~N~ và ~Q~ ~(N, Q \le 10^5)~ là số lượng phần tử và số lượng truy vấn;
• Dòng thứ hai gồm ~N~ số nguyên dương ~a_i \ (a_i\le 10^5; \ 1\le i\le N)~ mô tả dãy số;
• ~Q~ dòng sau, mỗi dòng gồm hai số nguyên dương ~l~ và ~r~ ~(1\le l\le r\le N)~ mô tả truy vấn.

Kết quả ghi ra tệp văn bản CSCH.OUT:

~Q~ dòng, mỗi dòng gồm một số nguyên là kết quả của truy vấn tương ứng.

Ví dụ

Input

5 2
3 1 3 3 4
2 4
1 5

Output

7
15

Giải thích

Ở truy vấn đầu tiên có các cặp chỉ số thoả mãn là: ~(2, 2), (3, 3), (4, 4), (3, 2), (4, 2), (3, 4), (4, 3)~

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm thoả mãn: ~N, Q \le 10^2~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~N \le 10^4; \ Q\le 10^2~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N \le 10^5; \ Q\le 10^2~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: dãy số ~a_1, a_2, \dots, a_N~ là hoán vị từ ~1~ đến ~N~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~l = 1~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm không có ràng buộc gì thêm.

Cho dãy số gồm ~N~ phần tử ~a_1, a_2, \dots, a_N~ là một hoán vị của các số nguyên từ ~1~ đến ~N~. Dãy con của một dãy số là dãy số nhận được khi không xoá phần tử nào hoặc xoá nhiều phần tử khỏi dãy số đó. Một dãy số ~b_1, b_2, \dots, b_M~ được gọi là dãy số lượn sóng khi thoả mãn điều kiện sau: Với mọi ~i \ (1\le i\le M-1)~, nếu ~b_i \lt b_{i+1}~ thì ~b_{i+1} \gt b_{i+2}~; hoặc nếu ~b_i \gt b_{i+1}~ thì ~b_{i+1} \lt b_{i+2}~. Dãy số gồm không quá ~2~ phần tử cũng là dãy số lượn sóng.

Ta gọi ~f(x, l, r)~ là số lượng phần tử của dãy con lượn sóng dài nhất của dãy số ~a_l, a_{l+1}, \dots, a_r~ sao cho tất cả các phần tử có giá trị không lớn hơn ~x~.

Đặt ~h(x) = \sum^N_{l=1} \sum^N_{r=l} f(x, l, r)~. Hãy tính các giá trị của ~h(1), h(2), \dots, h(N)~.

Dữ liệu vào từ tệp văn bản DSLS.INP:

• Dòng đầu tiên chứa số nguyên ~N \ (2\le N\le 2\times 10^5)~;
• Dòng thứ hai chứa ~N~ số nguyên ~a_i \ (1\le i\le n)~ là hoán vị từ ~1~ đến ~N~.

Kết quả ghi ra tệp văn bản DSLS.OUT:

Ghi trên ~N~ dòng, dòng thứ ~i \ (1\le i\le N)~ ghi một số nguyên là giá trị của ~h(i)~.

Ví dụ

Input

4
1 3 4 2

Output

4
8
14
18

Giải thích

~h(1) = 1 + 1 + 1 + 1 + 0 + 0 + 0 + 0 + 0 + 0 = 4~

~h(2) = 1 + 1 + 1 + 2 + 0 + 0 + 1 + 0 + 1 + 1 = 8~

~h(3) = 1 + 2 + 2 + 3 + 1 + 1 + 2 + 0 + 1 + 1 = 14~

~h(4) = 1 + 2 + 2 + 3 + 1 + 2 + 3 + 1 + 2 + 1 = 18~

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm thoả mãn: ~N\le 15~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N \le 100~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N \le 500~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~N\le 5000~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm không có ràng buộc gì thêm.

Cho một đơn đồ thị liên thông, vô hướng, có trọng số gồm:

• ~N~ đỉnh - được đánh số từ ~1~ đến ~N~;
• ~M~ cạnh - cạnh ~(u, v, c)~ mô tả đường đi hai chiều trực tiếp giữa hai đỉnh ~u~ và đỉnh ~v~, có chi phí là ~c~;
• ~K~ đỉnh đặc biệt, phân biệt có tính chất như sau: trên đường đi, khi ở một đỉnh đặc biệt có thể di chuyển đến một đỉnh đặc biết bất kỳ trước đó đã đi qua mà không mất chi phí.

Tìm đường đi có tổng chi phí nhỏ nhất đi qua toàn bộ các đỉnh đặc biệt (đường đi có thể xuất phát từ một đỉnh bất kì).

Dữ liệu vào từ tệp văn bản DDDB.INP:

• Dòng đầu tiên gồm ba số nguyên dương ~N, M~ và ~K \ (2\le K\le N; \ N, M\le 10^5)~ mô tả số lượng đỉnh, số lượng cạnh và số lượng đỉnh đặc biệt;
• Dòng thứ hai gồm ~K~ số nguyên dương ~S \ (S \le N)~ mô tả các đỉnh đặc biệt;
• ~M~ dòng sau, mỗi dòng gồm ba số nguyên dương ~u, v, c \ (u, v\le N; \ c\le 10^9)~ mô tả các cạnh của đồ thị.

Kết quả ghi ra tệp văn bản DDDB.OUT:

Một số nguyên duy nhất là tổng chi phí nhỏ nhất của đường đi thoả mãn yêu cầu.

Ví dụ

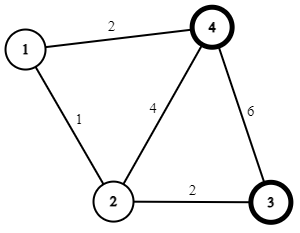
Input

4 5 2
4 3
1 2 1
2 3 2
4 1 2
4 2 4
3 4 6

Output

5

Giải thích

Có thể đi theo đường đi: ~4 \rightarrow 1 \rightarrow 2 \rightarrow 3~

---

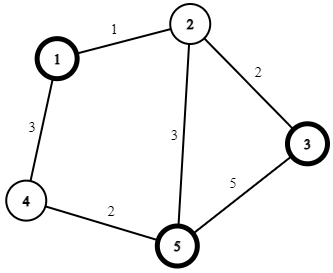
Input

5 6 3
5 1 3
1 2 1
2 3 2
4 1 3
4 5 2
5 2 3
3 5 5

Output

7

Giải thích

Có thể đi theo đường đi: ~1 \rightarrow 2 \rightarrow 3 \rightarrow 1\rightarrow 2\rightarrow 5~

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm thoả mãn: ~K=2; \ N\le 10^4~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~K=5; \ N\le 10^4~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~K=N~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm thoả mãn: ~N, M\le 10^3~;
• ~20\%~ số test khác ứng với ~20\%~ số điểm thoả mãn: ~M=N-1~;
• ~15\%~ số test khác ứng với ~15\%~ số điểm không có ràng buộc gì thêm.