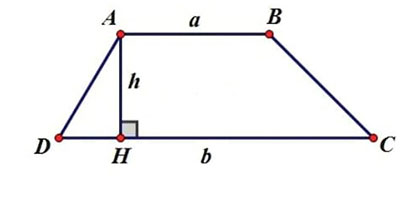
Cho ~a, b~ là độ dài 2 cạnh đáy và ~h~ là chiều cao của một hình thang. Tính diện tích hình thang đó.

Input

• Gồm một dòng chứa ~3~ số thực ~a, b, h~ (~a, b, h \leq 1000~).

Output

• In ra diện tích hình thang. Kết quả được tính đến chữ số thập phân thứ 3.

Sample Test

Input

5 3 2 

Output

8

Cho bốn số nguyên dương ~a, b, c, d~. Hãy so sánh ~\frac {a} {b}~ với ~\frac {c} {d}~.

Input

• Gồm một dòng chứa bốn số nguyên dương ~a, b, c, d~ (~a, b, c, d \leq 10^9~).

Output

• In ra > nếu ~\frac {a} {b} > \frac {c} {d}~.
• In ra < nếu ~\frac {a} {b} < \frac {c} {d}~.
• In ra = nếu ~\frac {a} {b} = \frac {c} {d}~.

Sample Test

Input

1 2 3 4

Output

<

Note

• ~\frac {1} {2} < \frac {3} {4}~.

Cho số nguyên dương ~N~. Đếm xem trong các chữ số của ~N~ có bao nhiêu số nguyên tố.

Input

• Gồm một số nguyên dương ~N~ duy nhất.
  
  

Output

• In ra số lượng chữ số là số nguyên tố trong ~N~.
  
  

Subtasks

• Subtask 1 (~50\%~ số điểm): ~N \leq 10^4~.
• Subtask 2 (~20\%~ số điểm): ~N \leq 10^8~.
• Subtask 3 (~30\%~ số điểm): ~N \leq 10^{100}~.
  
  

Sample Test

Input

23452345

Output

6

Note

• Có ~6~ chữ số nguyên tố trong ~N~ là ~2, 3, 5, 2, 3, 5~.

Cho một số tự nhiên ~N~. Hãy cho biết số ~N~ có là tổng của hai số tự nhiên liên tiếp hay không.

Input

Gồm một số tự nhiên ~N~ duy nhất. (~1 \leq N \le 10^9~)

Output

In ra YES nếu ~N~ là tổng của hai số tự nhiên liên tiếp, ngược lại in ra NO.

Sample Test 1

Input:

5

Output:

YES

Note: Do ~5 = 2 + 3~ nên ~5~ là tổng của hai số tự nhiên liên tiếp.

Sample Test 2

Input:

6

Output:

NO

Cho số nguyên dương ~n~, đếm số cách để chia ~n~ chiếc kẹo thành các phần bằng nhau (mà không phá vỡ hay làm hỏng chiếc kẹo nào).

Input

Gồm một số nguyên dương ~n~ duy nhất. (~n \leq 1000~)

Output

In ra số cách chia ~n~ chiếc kẹo thành các phần bằng nhau.

Sample Test

Input:

10

Output:

4

Giải thích: Các cách chia thoả mãn là:

• Chia thành ~1~ phần, mỗi phần ~10~ chiếc kẹo.
• Chia thành ~2~ phần, mỗi phần ~5~ chiếc kẹo.
• Chia thành ~5~ phần, mỗi phần ~2~ chiếc kẹo.
• Chia thành ~10~ phần, mỗi phần ~1~ chiếc kẹo.

Cho một số nguyên dương ~n~. Tính số ngày của năm ~n~, biết rằng năm ~n~ có thể là năm nhuận.

Input

Gồm một số nguyên dương ~n~ duy nhất. (~n \leq 3000~)

Output

In ra số ngày của năm ~n~.

Sample Test

Input:

2020

Output:

366

Nhập vào từ bàn phím một số thực là điểm trung bình của một học sinh lên. Biết rằng:

• Điểm trung bình từ ~8.0~ trở lên đạt loại Giỏi.
• Điểm trung bình từ ~6.5~ đến ~7.9~ đạt loại Khá.
• Điểm trung bình từ ~5.0~ đến ~6.4~ đạt loại Trung Bình.
• Điểm trung bình dưới ~5.0~ đạt loại Yếu.

Xác định học lực của bạn đó.

Input

Gồm một số thực có một chữ số ở phần thập phân trong khoảng ~[0, 10.0]~

Output

• In ra GIOI nếu học lực của bạn đó là Giỏi.
• In ra KHA nếu học lực của bạn đó là Khá.
• In ra TRUNGBINH nếu học lực của bạn đó là Trung Bình.
• In ra YEU nếu học lực của bạn đó là Yếu.

Sample Test

Input:

8.0

Output:

GIOI

Cho ~N~ số nguyên dương ~a_1, a_2, a_3, ..., a_N~. Tính trung bình cộng của ~N~ số đó.

Input

• Dòng đầu chứa số nguyên dương ~N~ (~N \leq 10^3~).
• Dòng thứ hai chứa ~N~ số nguyên dương ~a_1, a_2, a_3, ..., a_N~ (~a_i \leq 10^3~).

Output

• In ra trung bình cộng của ~N~ số đó. Kết quả được xét đến chữ số thập phân thứ 3.

Sample Test

5
1 2 4 3 5

Output

3

Dữ liệu đảm bảo để bài luôn có kết quả!

Cho dãy số có quy luật như sau: ~1,2,2,3,3,3,4,4,4,4,5,5,…~ Cho một số tự nhiên ~N~, hãy tìm số thứ ~N~ của dãy số trên (các số được đánh thứ tự từ ~1~).

Input

• Gồm một số nguyên dương ~N~ ~(N ≤ 10^{15})~.

Output

• In ra kết quả của bài toán.

Subtasks

• Subtask 1 (~60\%~ số điểm): ~N ≤ 10^{6}~;
• Subtask 2 (~20\%~ số điểm): ~N ≤ 10^{10}~;
• Subtask 3 (~20\%~ số điểm): Không có ràng buộc gì thêm.

Sample Test

Input

5

Output

3

Một số nguyên dương ~A~ được gọi là hoàn hảo nếu ~2 \times A \leq K~ (trong đó ~K~ là tổng các ước dương của ~A~).

Ví dụ: số ~12~ được coi là số hoàn hảo vì ~2 \times 12 \leq K~ với ~K = 1 + 2 + 3 + 4 + 6 + 12 = 28~

Cho ~N~ số nguyên dương ~A_1, A_2, \ldots, A_n~, hãy đếm số lượng số hoàn hảo trong dãy đã cho.

Input

• Dòng đầu tiên chứa số nguyên dương ~N~. (~N \leq 10^4~)
• ~N~ dòng tiếp theo, dòng thứ ~i~ chứa số nguyên dương ~A_i~. (~A_i \leq 10^6~)

Output

In ra số lượng số hoàn hảo trong dãy đã cho.

Sample Test

Input:

5
8
16
12
6
7

Output:

2

Cho ~N~ số nguyên ~A_1, A_2, \ldots, A_n~, hãy đếm số lượng số đơn lẻ trong dãy đã cho.

Số đơn lẻ trong dãy là số chỉ xuất hiện đúng một lần.

Input

• Dòng đầu tiên chứa số nguyên dương ~N~. (~N \leq 10^6~)
• ~N~ dòng tiếp theo, dòng thứ ~i~ chứa số nguyên ~A_i~. (~0 \leq A_i \leq 10^6~)

Output

• In ra số lượng số đơn lẻ trong dãy đã cho.

Sample Test

Input:

8
9
9
7
7
6
11
9
5

Output:

3

Cho một số tự nhiên ~N~. Hãy cho biết số ~N~ có là tổng của ~4~ số tự nhiên liên tiếp hay không, nếu có hãy đưa ra số nhỏ nhất trong ~4~ số đó.

Input

Gồm một số tự nhiên ~N~ duy nhất. (~N \le 10^9~)

Output

In ra số nhỏ nhất trong ~4~ số nếu ~N~ là tổng của ~4~ số tự nhiên liên tiếp, ngược lại in ra NO.

Sample Test 1

Input:

10

Output:

1

Note: Do ~10 = 1 + 2 + 3 + 4~ nên ~10~ là tổng của bốn số tự nhiên liên tiếp.

Sample Test 2

Input:

12

Output:

NO

Trong phòng thí nghiệm, các nhà khoa học đang nghiên cứu về gen của một chuỗi ARN đặc biệt được mã hóa bằng một xâu ~S~ gồm các kí tự ~'A', \ 'U', \ 'G', \ 'X'~. Họ muốn cắt từ chuỗi ARN đó một mạch (được mã hóa bằng xâu ~X~ cho trước).

Yêu cầu: Từ chuỗi ARN ~S~ có thể cắt được ra tối đa bao nhiêu đoạn mạch ~X~.

Dữ liệu:

• Dòng đầu tiên gồm một xâu kí tự ~S~ mô tả chuỗi ARN~;~
• Dòng thứ hai gồm một xâu kí tự ~X~ mô tả đoạn mạch cần cắt ra.

Các xâu chỉ gồm các kí tự ~'A', \ 'U', \ 'G', \ 'X'~ và độ dài các xâu không quá ~10^3~ kí tự.

Kết quả:

Một số nguyên duy nhất là kết quả của bài toán.

Ví dụ

Input

AUAUGXXAUGXGX
AUGX

Output

2

Giải thích: AUAUGXXAUGXGX

Input

AAAAA
AAA

Output

1

Giải thích: AAAAA

Input

AGAX
U

Output

0

Dino chọn tất cả các số tự nhiên từ ~a~ đến ~b~. Daisy chọn tất cả các số tự nhiên từ ~c~ đến ~d~. Hỏi hai bạn có chọn số nào giống nhau không?

Input

Gồm bốn dòng, mỗi dòng chứa lần lượt các số nguyên ~a~, ~b~, ~c~, ~d~. (~0 \leq a \leq b \leq 1000~, ~0 \leq c \leq d \leq 1000~)

Output

In ra YES nếu hai bạn chọn có số chung, ngược lại in ra NO.

Sample Test 1

Input:

5 
10 
15 
20

Output:

NO

Note:

• Dino chọn các số từ ~5~ đến ~10~: ~5, 6, 7, 8, 9, 10~
• Daisy chọn các số từ ~15~ đến ~20~: ~15, 16, 17, 18, 19, 20~
• Do các số hai bạn chọn không giống nhau nên kết quả là NO.

Sample Test 2

Input:

1 
4
2
6

Output:

YES

Note:

• Dino chọn các số từ ~1~ đến ~4~: ~1, 2, 3, 4~
• Daisy chọn các số từ ~2~ đến ~6~: ~2, 3, 4, 5, 6~
• Do các số hai bạn cùng chọn số ~2, 3, 4~ nên kết quả là YES.

Cho một robot được lập trình di chuyển trên một hàng ngang gồm các ô vuông. Mỗi ô được đặt tên bằng các kí tự theo thứ tự từ ~'𝐴'~ đến ~'𝑍'~ và được lặp lại vô hạn. Ban đầu robot xuất phát ở ô thứ ~1~ có tên là ~'𝐴'~ và nhảy đến các ô tiếp theo quy luật: lần ~1~ nhảy ~1~ ô, lần ~2~ nhảy ~2~ ô, lần ~3~ nhảy ~3~ ô, ~…~, lần ~𝑁~ nhảy ~𝑁~ ô. Vậy sau ~𝑁~ lần nhảy thì robot đang ở ô nào?

Dữ liệu:

Gồm một số nguyên dương ~N~ là số lần nhảy của robot ~(N \le 10^9)~.

Kết quả:

Một kí tự duy nhất là tên của ô sau ~N~ lần robot nhảy.

Ràng buộc

• Có ~60\%~ số test ứng với ~60\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10^3;~
• ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thoả mãn: ~𝑁 ≤ 10^6;~
• ~20\%~ số test còn lại ứng với 20% số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

1

Output

B

Giải thích: Sau ~1~ lần nhảy, robot ở ô thứ ~2~, có tên là kí tự ~B~.

Input

4

Output

K

Giải thích: Sau ~4~ lần nhảy, robot ở ô thứ ~11~, có tên là kí tự ~K~.

Input

7

Output

C

Giải thích: Sau ~7~ lần nhảy, robot ở ô thứ ~29~, có tên là kí tự ~C~.

Cho một dãy số nguyên ~A~ gồm ~N~ phần tử ~A_1,A_2,…,A_N~. In ra độ dài của dãy con liên tiếp đan dấu dài nhất. (Đan dấu là không có hai phần tử nào cạnh nhau mà có cùng dấu)

Input:

• Dòng đầu tiên gồm một số nguyên dương ~N~ ~(N≤10^5)~ là số lượng phần tử của dãy ~A~.
• Dòng thứ hai gồm ~N~ số nguyên ~A_1,A_2,…,A_N~ mô tả dãy ~A~ ~(0<|A_i|≤10^9)~.

Output:

Ghi ra một số nguyên duy nhất là độ dài của dãy con liên tiếp đan dấu dài nhất.

Ràng buộc

• Có ~60\%~ số test ứng với ~60\%~ số điểm có ~N≤10^3~;
• ~40\%~ số test còn lại ứng với ~40\%~ số điểm không có ràng buộc gì thêm.

Sample Test 1

Input:

9
1 3 -1 3 -2 4 -5 -6 7

Output

6

Giải thích

Dãy đan dấu: 3 -1 3 -2 4 -5

Sample Test 2

Input:

9
1 3 -1 3 -2 4 -5 6 7

Output

7

Giải thích

Dãy đan dấu 3 -1 3 -2 4 -5 6

Dino và Daisy đang chơi một trò chơi, ban đầu Dino có ~A~ điểm và Daisy có ~B~ điểm. Mỗi phút, mỗi bạn được tăng lên ~1~ điểm. Hỏi sau bao nhiêu phút thì số điểm của Dino gấp ~3~ lần số điểm của Daisy? Nếu điểm của Dino không thể gấp ~3~ lần điểm của Daisy thì in ra NO.

Input

• Dòng ~1~ chứa một số tự nhiên ~A~ là số điểm ban đầu của Dino;
• Dòng ~2~ chứa một số tự nhiên ~B~ là số điểm ban đầu của Daisy.

Output

• Ghi ra kết quả của bài toán.

Example

Sample input 1

9
1

Sample output 1

3

Giải thích

Sau 3 phút thì số điểm của Dino là ~9+3=12~, điểm của Daisy là ~1+3=4~. Khi đó điểm của Dino gấp ~3~ lần điểm của Daisy.

Sample input 1

4
2 

Sample output 1

NO

Giới hạn

• Nếu chương trình chạy đúng những trường hợp ~A, B \leq 1000~, thí sinh sẽ được ~60~ điểm;
• Nếu chương trình chạy đúng những trường hợp ~A, B \leq 10^9~, thí sinh sẽ được ~100~ điểm;

Cho một dãy gồm ~N~ số nguyên ~a_1, a_2, a_3, ..., a_N~. Hãy tìm đoạn con liên tiếp và dài nhất mà các phần tử liên tiếp cách đều nhau.

Input

• Dòng thứ nhất chứa số nguyên dương ~N~.
• Dòng thứ hai chứa ~N~ số nguyên ~a_1, a_2, a_3, ... a_N~. (~|a_i| \leq 10^9~)

Output

• In ra độ dài của đoạn con dài nhất thoả mãn đề bài.

Subtasks

• Subtask 1 (~20\%~ số điểm): ~N = 3~.
• Subtask 2 (~30\%~ số điểm): ~N \leq 10^3~.
• Subtask 3 (~50\%~ số điểm): ~N \leq 10^6~.

Sample Test 1

Input

3
1 2 1

Output

3

• Dãy đã cho có các số liên tiếp cách nhau ~1~ đơn vị nên đây là dãy con dài nhất thoả mãn.

Sample Test 2

Input

6
1 2 3 5 7 9

Output

4

Note

• Dãy con liên tiếp dài nhất và cách đều nhau là ~3, 5, 7, 9~. (khoảng cách giữa các số liên tiếp đều là ~2~)

Sample Test 3

Input

6
1 4 7 4 7 1

Output

5

Note

• Dãy con liên tiếp dài nhất và cách đều nhau là ~1, 4, 7, 4, 7~. (khoảng cách giữa các số liên tiếp đều là ~3~)

Tên tệp của một file Python bắt buộc gồm hai phần, ngăn cách bởi một dấu chấm .:

• Phần tên: Là một xâu không rỗng, gồm các kí tự từ a đến z, A đến Z, 0 đến 9, dấu gạch dưới (_) hoặc dấu gạch ngang (-).
• Phần mở rộng: Là xâu py, không phân biệt chữ hoa chữ thường.

Ví dụ:

• Tên file Python hợp lệ: a.py, Hello-world.py, tXz_69420.Py.
• Tên file Python không hợp lệ: among us.py (chứa dấu cách), 6/9/2022.py (chứa dấu /), pa064.cpp (sai phần mở rộng).

Bạn được cho một xâu, hãy kiểm tra xem xâu đó liệu có thể là tên hợp lệ cho một file Python không nhé.

Input

Gồm một xâu S khác rỗng có độ dài không quá 100 ký tự thuộc bảng mã ACSII.

Output

In ra YES nếu S là tên file Python hợp lệ, ngược lại in ra NO.

Sample Test 1:

Input:

helloWorld.py

Output:

YES

Sample Test 2:

Input:

pythonIntro.docx

Output:

NO

Sample Test 3:

Input:

test_ko_sai_nhe_hehe.py

Output:

YES

TDZ rất thích con số ~42~, vì nó là số trước số ~43~ và số sau số ~41~. Với ước mơ tương lai trở thành một giáo sư đại tài, cậu quyết định đi nghiên cứu sâu hơn số ~42~ này.

Cậu lấy số ~42~ này nhân đôi lên, lấy 2 chữ số cuối của kết quả tìm được tiếp tục nhân đôi tiếp. Quá trình này diễn ra vô tận. Sau ~N~ lần lặp lại như thế, cậu đã tìm ra một phát hiện mới mẻ. Đố các bạn, sau ~N~ lần TDZ đã thu được số nào?

Input

Gồm một số tự nhiên ~N~ duy nhất.

Output

In ra số TDZ thu được sau khi lặp lại quá trình nhân đôi ~N~ lần.

Subtasks

Subtask ~1~ (~50\%~ số điểm): ~N \leq 10^3~.

Subtask ~2~ (~50\%~ số điểm): ~N \leq 10^9~.

Sample Test

Input:

3

Output

36

Note:

• Nhân đôi lần ~1~ được ~42 \times 2 = 84~.
• Nhân đôi lần ~2~ được ~84 \times 2 = 168~, lấy hai chữ số cuối được ~68~.
• Nhân đôi lần ~3~ được ~68 \times 2 = 136~, láy hai chữ số cuối được ~36~.

Xét hai số nguyên dương ~u, v~, ta gọi thao tác ghép hai số ~u, v~ là thao tác viết số ~v~ sau số ~u~.

Ví dụ: Với ~u = 123, v = 456~, sau khi ta ghép hai số ~u, v~ với nhau, ta được số ~123456~.

Cho ~n~ số nguyên dương ~a_1, a_2, ..., a_n~.

Hãy cho biết: Có bao nhiêu cặp chỉ số ~(i, j) \ (1 \le i \lt j \le n)~ sao cho khi ta thực hiện thao tác ghép hai số ~a_i, a_j~, ta được một số mới chia hết cho ~3~?

Input

• Dòng đầu tiên chứa số nguyên dương ~n \ (n \ge 2);~
• Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n.~

Output

In ra kết quả là số cặp chỉ số ~(i, j)~ thoả mãn đề bài.

Scoring

• Subtask 1 [20%]: ~n \le 1000; \ a_i \le 10^9;~
• Subtask 2 [40%]: ~n \le 10^5; \ a_i \le 10^{18};~
• Subtask 3 [40%]: ~n \le 10^5; \ a_i \le 10^{100}.~

Examples

Input

7
123 4 5 7 10 3 2

Output

7

Giải thích: Các cặp chỉ số thoả mãn yêu cầu đề bài là: ~(1, 6), (2, 3), (2, 7), (3, 4), (3, 5), (4, 7), (5, 7).~

TDZ đang tham gia một contest trên trang web HNOJ. Contest này gồm ~N~ bài, mỗi bài có điểm tối thiểu là ~2~ và điểm tối đa là ~5~.

Tuy nhiên, TDZ lại gặp vài vấn đề:

• Nếu điểm của TDZ vượt quá ~k~, cậu sẽ bị chọn đi thi HSG, tuy nhiên cậu lại rất lười và thích ở nhà chơi game hơn là thi cử.
• Nếu điểm của TDZ thấp hơn ~k~, mẹ của cậu sẽ cảm thấy rất buồn.

Vì vậy, TDZ quyết định sẽ đạt được chính xác ~k~ điểm trong contest.

Thực ra cậu là một thiên tài xuất chúng ẩn dật nên có thể tự quyết định mình được bao nhiêu điểm mỗi bài. Nhưng cậu lại rất ghét việc đạt điểm thấp mỗi bài, nên cậu sẽ cố gắng hạn chế việc bị ~2~ điểm nếu có thể.

Hãy giúp TDZ tính xem cậu cần phải đạt tối thiểu bao nhiêu điểm ~2~ trong contest để điểm cả contest đạt được chính xác ~k~ điểm.

Input

Gồm một dòng chứa hai số nguyên ~N~ và ~k~. (~1 \le N \leq 50~; ~2 \times N \le k \le 5 \times N~)

Output

Số bài tối thiểu trong contest phải đạt ~2~ điểm để TDZ có thể đạt được chính xác ~k~ điểm.

Sample Test 1

Input:

4 8

Output:

4

Note: TDZ bắt buộc phải đạt ~2~ điểm cả ~4~ bài để cả contest được ~8~ điểm.

Sample Test 2

Input:

4 10

Output:

2

Note: TDZ có thể đạt ~2~ điểm ở hai bài đầu và ~3~ điểm ở hai bài còn lại.

Sample Test 3

Input:

1 3

Output:

0

Note: TDZ chỉ đạt ~3~ điểm cho một bài duy nhất trong contest.

Cho dãy số nguyên ~a~ gồm ~n~ phần tử. Hãy tính tổng của ~|a_i-a_j|~ với mọi cặp ~(i,j)~ thỏa mãn ~1 \le i < j \le n~.

Input

• Dòng đầu gồm ~1~ số nguyên ~n~ ~(1 \le n \le 10^5)~.
• Dòng sau gồm ~n~ số nguyên miêu tả dãy ~a~ ~(|a_i| \le 10^6)~

Output

• In ra kết quả tìm được.

Sample Test

Input

3
5 1 2

Output

8

Đây là phiên bản khó hơn của bài PA120. Điểm khác biệt duy nhất giữa hai bài là số ~k~ và giới hạn các số.

Sau khi bán hết sách, TDZ chuyển sang mở một quán cà phê.

Qua thăm dò, TDZ đã biết trước ngày khai trương sẽ có ~n~ khách, khách thứ ~i~ sẽ vào thời điểm ~h_i~. Để phục vụ lượng khách đến dồn dập, quán cà phê có thuê thêm một số nhân viên ưu tú. Mỗi nhân viên có thể hoạt động không ngừng nghỉ, mỗi lần chỉ phục vụ một khách trong đúng ~k~ đơn vị thời gian. Nhưng nếu một vị khách tới mà không nhận được sự phục vụ ngay thì sẽ lập tức bỏ đi.

Cụ thể, một vị khách đến ở thời điểm ~x~ nào đó, thì nhân viên sẽ phục vụ xong cho vị khách đó ở thời điểm ~x + k~. Khách đó sẽ rời quán và nhân viên tiếp tục phục vụ luôn khách tiếp theo (nếu có).

Hãy giúp TDZ tìm ra số lượng nhân viên cần thuê ít nhất mà vẫn đảm bảo tất cả các khách đều được phục vụ.

Input

• Dòng đầu tiên chứa 2 số nguyên dương ~n~, ~k~ (~n \leq 10^6, k \leq 10^9~).
• Dòng tiếp theo chứa ~n~ số nguyên dương ~h_1, h_2, h_3, \ldots, h_n~ tương ứng với thời điểm khách đến (~h_i \leq 10^9~).

Output

In ra số lượng nhân viên ít nhất cần thuê.

Subtasks

• Subtask ~1~ (~25\%~): ~n \leq 10^3~.
• Subtask ~2~ (~37.5\%~): ~n \leq 10^6, h_i \leq 10^6~.
• Subtask ~3~ (~37.5\%~): Không có điều kiện gì thêm.

Sample Test

Input:

5 2
1 2 5 3 5

Output:

2

Note: Thuê hai nhân viên:

• Nhân viên thứ nhất sẽ phục vụ khách thứ nhất, rồi đến khách thứ tư và cuối cùng phục vụ khách thứ ba.
• Nhân viên thứ hai phục vụ khách thứ hai rồi đến khách thứ năm.

Viết liền các số nguyên dương liên tiếp, từ nhỏ đến lớn, bắt đầu từ ~1~, ta sẽ được một dãy dài vô hạn gồm các chữ số: ~123456789101112131415161718192021222324252627282930313233343536\ldots~

Bạn được cho số nguyên dương ~k~, nhiệm vụ của bạn là tìm chữ số thứ ~k~ của dãy trên.

Input

• Dòng thứ nhất chứa số nguyên dương ~T~ - số bộ dữ liệu. (~T \leq 10^3~)
• ~T~ dòng tiếp theo, mỗi dòng chứa một số nguyên dương ~k~.

Output

• In ra ~T~ dòng, mỗi dòng chứa một chữ số cho bộ dữ liệu tương ứng.

Subtasks

• Subtask 1 (~20\%~ số điểm): Mọi số ~k \leq 50~.
• Subtask 2 (~30\%~ số điểm): Mọi số ~k \leq 10^6~.
• Subtask 3 (~50\%~ số điểm): Mọi số ~k \leq 10^{18}~.

Sample Test

Input

5
8
18
16
14
19

Output

8
1
1
1
4

Cho ~N~ số tự nhiên ~a_1, a_2, a_3, \dots, a_n~. Hãy đếm số lượng chữ số ~0~ tận cùng có nghĩa của tích ~a_1 \times a_2 \times a_3 \times \dots \times a_n~.

Input

• Dòng đầu tiên chứa số ~N~.
• Dòng thứ hai chứa ~N~ số tự nhiên ~a_1, a_2, a_3, \dots, a_n~.

Output

• In ra số lượng số chữ số ~0~ tận cùng có nghĩa của ~N~ số đã cho.

Subtasks

• Subtask ~1~ (~50\%~ số điểm): ~N \leq 18, a_i \leq 10~.
• Subtask ~2~ (~50\%~ số điểm): ~N \leq 100, a_i \leq 10^9~.

Sample Test

Input:

5
2 5 4 9 10

Output:

2

Note:

• ~2 \times 5 \times 4 \times 9 \times 10 = 3600~ có ~2~ chữ số ~0~ tận cùng có nghĩa.

Cho số nguyên dương ~k~. Đếm số cặp ~(a, b)~ thoả mãn ~a, b~ là hai số nguyên dương và ~a^2 + b^2 \leq k~.

Lưu ý: Hai cặp ~(a, b)~ và ~(b, a)~ được coi là hai cặp khác nhau.

Input

• Gồm một số nguyên dương ~k~ duy nhất.

Output

• In ra số cặp ~(a, b)~ thoả mãn.

Subtasks

• Subtask ~1~ (~30\%~ số điểm): ~k \leq 10^3~;
• Subtask ~2~ (~20\%~ số điểm): ~10^3 < k \leq 10^6~;
• Subtask ~3~ (~50\%~ số điểm): ~10^6 < k \leq 10^{12}~.

Sample Test

Input:

8

Output:

4

Note: Các cặp thoả mãn là ~(1, 1); (1, 2); (2, 1); (2, 2)~.

Một số ~X~ ban đầu được tách thành ~N~ số ~A_1, A_2, \ldots, A_n~. Hãy tìm cách ghép lại ~N~ số này, theo thứ tự bất kỳ, thành số lớn nhất có thể.

Input

• Dòng đầu tiên chứa số nguyên dương ~N~ (~N \leq 100~).
• ~N~ dòng tiếp theo, dòng thứ ~i~ chứa số ~A_i~ (độ dài số ~A_i~ không vượt quá ~100~). Lưu ý, ~A_i~ có thể có các chữ số ~0~ đứng ở đầu.

Output

• In ra số lớn nhất có thể tạo được từ việc ghép ~N~ số đã cho. Số này có thể có các chữ số ~0~ đứng ở đầu.

Sample Test

Input:

4
2
20
004
66

Output:

66220004

Cho số nguyên dương ~N~. Hãy đếm số cách xoá đi một đoạn chữ số liên tiếp của ~N~ (không được xoá hết) để nhận được số mới chia hết cho ~3~, biết rằng số mới nhận được có thể có thừa chữ số ~0~ ở đầu.

Hai cách xoá được coi là khác nhau nếu có một vị trí được xoá trong cách này nhưng không được xoá trong cách kia.

Input

• Gồm một dòng duy nhất chứa một số nguyên ~N~ (~1 \le N \le 10^{100000}~).

Output

• In ra một số nguyên là số cách xoá tìm được.

Subtasks

• Subtask 1 (~50\%~ số điểm): ~N \le 10^{300}~.
• Subtask 2 (~25\%~ số điểm): ~N \le 10^{10000}~.
• Subtask 3 (~25\%~ số điểm): Không có ràng buộc gì thêm.

Sample Test 1

Input

1005

Output

4

Sample Test 2

Input

2009

Output

3

Cho số ~n~ và dãy số nguyên ~a~ gồm ~n~ phần tử, hãy tìm đoạn con liên tiếp dài nhất của dãy ~a~ có trung bình cộng lớn hơn hoặc bằng ~k~ cho trước.

Input

• Dòng đầu gồm 2 số nguyên ~n~ ~(1 \le n \le 10^5)~ và ~k~ ~(|k| \le 10^6)~.
• Dòng sau gồm ~n~ số nguyên miêu tả dãy ~a~ ~(|a_i| \le 10^6)~

Output

• In ra một số nguyên là độ dài của dãy con liên tiếp dài nhất thỏa mãn.

Sample Test

Input

7 3
1 5 2 3 1 4 1

Output

5

Cho ba số nguyên dương ~c~, ~d~, ~x~. Bạn cần phải tìm số cặp ~(a,b)~ thỏa mãn ~c*lcm(a,b) - d*gcd(a,b) = x~. Ở đây, ~lcm(a,b)~ là bội chung nhỏ nhất của ~(a,b)~, ~gcd(a,b)~ là ước chung lớn nhất của ~(a,b)~.

Input

• Dòng đầu gồm số nguyên dương ~t~ ~(t \le 10^4)~ là số lượng test case.
• ~t~ dòng sau, mỗi dòng gồm ba số nguyên dương ~c~, ~d~, ~x~ miêu tả test case. ~(1 \le c,d,x \le 10^7)~

Output

• Với mỗi test case, in ra số lượng cặp ~(a,b)~ thỏa mãn.

Sample Test

Input

4
1 1 3
4 2 6
3 3 7
2 7 25

Output

4
3
0
8

Giải thích: Ở test case thứ nhất, có ~4~ cặp thỏa mãn là ~(1,4), (4,1), (3,6), (6,3)~

Cho dãy ~A~ gồm ~n~ phần tử, phần tử thứ ~i \ (1 \le i \le n)~ có giá trị ~a_i~.

Bạn có thể biến đổi dãy ~A~ bằng thao tác sau: Chọn hai phần tử liên tiếp trong dãy và thay thế hai phần tử này bằng tổng của chúng.

Hãy đếm số lượng thao tác tối thiểu để dãy ~A~ là dãy đối xứng. Dãy ~A~ được coi là dãy đối xứng nếu đọc từ phải sang trái vẫn thu được dãy ~A~ ban đầu.

Input

• Dòng đầu tiên chứa số nguyên dương ~n;~
• Dòng tiếp theo chứa ~n~ số nguyên dương ~a_i \ (1 \le a_i \le 10^9)~.

Output

In ra kết quả là số thao tác tối thiểu để dãy ~A~ là dãy đối xứng.

Scoring

• Subtask 1 [30%]: ~n \le 10;~
• Subtask 2 [30%]: ~n \le 1000;~
• Subtask 3 [40%]: ~n \le 10^6.~

Examples

Input

3
1 2 3

Output

1

Giải thích: ~\textbf{1 2} \ 3 \rightarrow 3 \ 3.~

Input

5
1 2 4 6 1

Output

1

Giải thích: ~1 \ {\textbf{2 4}} \ 6 \ 1 \rightarrow 1 \ 6 \ 6 \ 1~.

Input

4
1 4 3 2

Output

2

Giải thích: ~\textbf{1 4} \ 3 \ 2 \rightarrow 5 \ \textbf{3 2} \ \rightarrow 5 \ 5~.