Bài ôn tập tổng hợp số 2 8/12/2025
Tổng đoạn
Nộp bàiPoint: 5
Cho hai số nguyên dương ~l, r~. Hãy tính giá trị của ~\displaystyle\sum_{i=l}^rS(i)~, biết rằng ~S(n)~ được định nghĩa là tổng các số nguyên dương từ ~1~ đến ~n~.
Input
Một dòng duy nhất gồm hai số nguyên ~l, r \ (1 \le l \le r \le 10^{12}).~
Output
In ra kết quả cần tìm sau khi chia lấy dư cho ~10^9 + 7~.
Scoring
- Subtask 1 [25%]: ~l \le r \le 500;~
- Subtask 2 [25%]: ~r - l \le 10^6;~
- Subtask 3 [25%]: ~l = 1;~
- Subtask 4 [25%]: Không có ràng buộc gì thêm.
Examples
Input
3 5
Output
31
Giải thích
~S(3) + S(4) + S(5) = (1 + 2 + 3) + (1 + 2 + 3 + 4) + (1 + 2 + 3 + 4 + 5) = 31.~
Số Siêu Nguyên Tố
Nộp bàiPoint: 5
Số siêu nguyên tố là số nguyên tố có tổng các chữ số cũng là số nguyên tố. Ví dụ: số ~5, 23~ là số siêu nguyên tố.
Hãy đếm số số siêu nguyên tố trong đoạn ~[m \to n]~ ~(m, n \le 10^6)~
INPUT
2 số nguyên dương ~m~, ~n~ (~0~ ~\le~ ~m~, ~n~ ~\le~ ~10^6~)
OUTPUT
Số nguyên dương duy nhất thoả mãn yêu cầu đề bài.
SAMPLE INPUT
5 20
SAMPLE OUTPUT
3
NỐI DÂY TERA
Nộp bàiPoint: 6
Đề thi vào trường mẫu giáo SuperBabies khá đơn giản: Có ~n~ đoạn dây xanh, ~n~ đoạn dây đỏ, ~n~ đoạn dây tím và ~n~ đoạn dây vàng. Độ dài các đoạn dây được cho trước.
Mỗi bé được cho một số nguyên ~l~ và cần cho biết có bao nhiêu cách chọn đúng ~1~ đoạn dây xanh, ~1~ đoạn dây đỏ, ~1~ đoạn dây tím và ~1~ đoạn dây vàng để nối lại thành một sợi dây trang trí có độ dài bằng ~l~. Hai cách chọn được gọi là khác nhau nếu có đoạn dây được chọn trong một cách nhưng không được chọn trong cách còn lại.
Yêu cầu: Viết chương trình tìm đáp án để chấm cho các bé.
INPUT
Dòng 1 chứa hai số nguyên dương ~n \le 1000, l \le 10^9~
Dòng 2 chứa ~n~ số nguyên dương là độ dài ~n~ đoạn dây xanh
Dòng 3 chứa ~n~ số nguyên dương là độ dài ~n~ đoạn dây đỏ
Dòng 4 chứa ~n~ số nguyên dương là độ dài ~n~ đoạn dây tím
Dòng 5 chứa ~n~ số nguyên dương là độ dài ~n~ đoạn dây vàng
Độ dài các đoạn dây không quá ~10^9~
OUTPUT
Số nguyên duy nhất là số cách chọn tính được.
SAMPLE INPUT
3 28
1 1 1
1 1 1
10 11 12
13 14 15
SAMPLE OUTPUT
18
Bảng lớn nhất
Nộp bàiPoint: 6
Khuyến khích các bạn giải bài Mua đất trước khi làm bài này.
Cho hai dãy ~a, b~ lần lượt có độ dài ~n, m~.
Gọi ~c~ là bảng có kích thước ~n \times m~, trong đó ~c_{ij} = a_i \times b_j~ ~(c_{ij}~ có nghĩa là ô vuông ở hàng thứ ~i~, cột thứ ~j~ của bảng ~c)~.
Hãy tìm hình chữ nhật con có diện tích lớn nhất sao cho tổng các phần tử của nó không vượt quá ~x~. Nói cách khác, hãy tìm số nguyên ~S~ lớn nhất thoả mãn tồn tại ~4~ số nguyên dương ~x_1, y_1, x_2, y_2~ thoả mãn ~1 \le x_1 \le x_2 \le n; \ 1 \le y_1 \le y_2 \le m; \ (x_2 - x_1 + 1) \times (y_2 - y_1 + 1) = S,~ và: $$\sum_{i=x_1}^{x_2}\sum_{j=y_1}^{y_2}C_{ij} \le x.$$
Input
- Dòng đầu tiên gồm ba số nguyên dương ~n, m, x \ (1 \le x \le 2 \times 10^9);~
- Dòng thứ hai gồm ~n~ số nguyên ~a_1, a_2, ..., a_n \ (1 \le a_i \le 1000; \ 1 \le i \le n);~
- Dòng thứ ba gồm ~m~ số nguyên ~b_1, b_2, ..., b_n \ (1 \le b_i \le 1000; \ 1 \le i \le m).~
Output
Một số nguyên là kết quả của bài toán. Nếu không có hình chữ nhật con nào thoả mãn thì in ra ~0~.
Subtasks
- Subtask 1 [20%]: ~1 \le n, m \le 50;~
- Subtask 2 [40%]: ~1 \le n, m \le 500;~
- Subtask 3 [40%]: ~1 \le n, m \le 5000.~
Examples
Input
3 3 9
1 2 3
1 2 3
Output
4
Giải thích
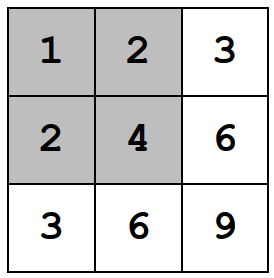
Input
5 1 5
5 4 3 4 5
2
Output
0
Giải thích
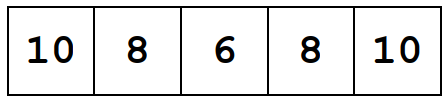
Phần quà đặc biệt
Nộp bàiPoint: 8
Cũng trong nhân dịp đạt được ~100~ triệu subscribers này của TDZ , T đã chọn ra subscriber thứ ~100~ triệu của mình và mời người đó tham gia trò chơi chọn quà. Rất may mắn là bạn chính là subscriber thứ ~100~ triệu của TDZ!
Sau khi gặp gỡ và trò chuyện với T, bạn được T phổ biến về trò chơi. Nội dung của trò chơi như sau: Có ~n~ phần quà trên bàn, mỗi phần quà có giá trị ~a_i \ (1 \le i \le n)~. Bạn sẽ được thực hiện thao tác chọn quà như sau nhiều lần: Đầu tiên, bạn chọn một phần quà bất kỳ trên bàn, giả sử nó có giá trị là ~x~. Khi đó, tất cả những phần quà có giá trị là ~x - 1~ và ~x + 1~ sẽ bị lấy ra khỏi bàn. Trò chơi kết thúc khi bạn không thể thực hiện thao tác chọn quà bất cứ một lần nào nữa và bạn sẽ được mang về tất cả những phần quà còn lại trên bàn.
Hãy tối ưu cách chơi của bạn để tổng giá trị của các phần quà bạn mang về là lớn nhất.
Input
- Dòng đầu tiên chứa số nguyên dương ~n \ (n \le 10^5);~
- Dòng tiếp theo chứa ~n~ số nguyên ~a_i \ (1 \le a_i \le 10^5, \ 1 \le i \le n).~
Output
In ra kết quả là tổng giá trị phần quà lớn nhất mà bạn có thể mang về được trong trò chơi.
Examples
Input
3
1 3 2
Output
4
Giải thích: Cách chọn quà tối ưu như sau:
- Chọn phần quà có giá trị là ~1 \rightarrow~ Các phần quà có giá trị là ~2~ bị bỏ ra khỏi bàn.
- Chọn phần quà có giá trị là ~3~.
Khi đó, tổng giá trị các phần quà bạn có thể mang về là: ~1 + 3 = 4~.
Input
5
4 1 1 2 3
Output
6
Giải thích: Cách chọn quà tối ưu như sau:
- Chọn phần quà có giá trị là ~2 \rightarrow~ Các phần quà có giá trị là ~1~ và ~3~ bị bỏ ra khỏi bàn.
- Chọn phần quà có giá trị là ~4~.
Khi đó, tổng giá trị các phần quà bạn có thể mang về là: ~4 + 2 = 6~.
Input
5
6 6 6 6 6
Output
30
Giải thích: Bạn có thể lấy cả ~5~ phần quà trên bàn mà không phải bỏ phần quà nào.